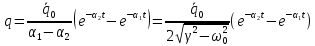1.Квазистационарность, Уравнение колебательного контура.

Колебания - всякий периодический или приблизительно периодический процесс, в котором значения той или иной физической величины повторяются точно или приближенно через равные или приблизительно равные промежутки времени.

Квазистационарность означает что мгновенные значения тока 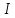практически одинаковы на всех участках проводов, соединяющих обкладки конденсатора. Для этого все изменения во времени должны происходить настолько медленно, чтобы распространение электродинамических взаимодействий можно

было считать мгновенным. Такие взаимодействия распространяются со скоростью, которая по порядку величины совпадает со скоростью света в вакууме 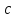. Обозначим через длину провода, соединяющего

обкладки конденсатора (практически эта величина совпадает с длиной провода, из которого изготовлена обмотка катушки самоиндукции). На прохождение длины 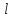электромагнитное возмущение затрачивает время порядка 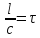. Условие квазистационарности будет выполнено,

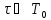если или 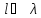, где 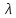— длина электромагнитной волны в вакууме:

Если выполняется обратное неравенство то такие системы называются распределенными.

Колебательный контур-система, состоящая из последовательно соединенных конденсатора, катушки самоиндукции и проводника с омическим сопротивлением (Рис).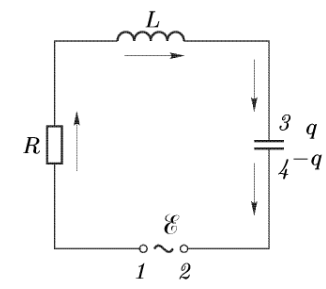

Применим к этому контуру уравнение Максвелла: .

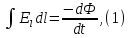Пусть выполнено условие квазистационарности. Тогда, применяя к участку 13 закон Ома, найдем: 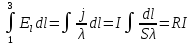, где 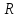— омическое сопротивление этого участка. Cсопротивление участка 42 пренебрежимо мало, то интеграл по пути 32 равен напряжению 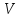между обкладками конденсатора:

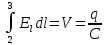
- подводимое напряжение-

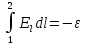
В результате первое уравнение примет вид:

.

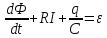Для квазистационарных токов :

Уравнение колебательного контура:

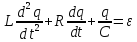
2.Свободные колебания гармонического осциллятора:

Если нет в системе омического сопротивления, то свободные колебания описываются уравнением:

Всякая система — механическая, электрическая или какая-либо другая, свободные колебания которой подчиняются (1) уравнению называется гармоническим осциллятором.

Для решения (1) умножим обе части на :

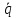Величина 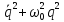не изменяется во времени, так как эта величина есть сумма двух квадратов, то она существенно положительна и может быть представлена в виде:

,

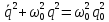где 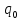—постоянная. Это равенство выражает сохранение энергии, так как его можно записать в виде:

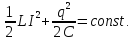
Чтобы выполнить второе интегрирование, разделим переменные:

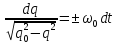
Отсюда: 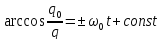или

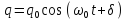
3.Затухающие колебания:

Учитывая силы сопротивления 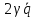– система называется гармоническим осциллятором с затуханием.

Для решения введем новую переменную 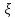, пологая:

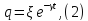
Тогда:

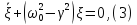
Здесь коэффициент 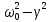может принимать и положительное и отрицательное значение. Три случая:

Случай 1: , введем обозначение

Тогда:

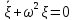
Отсюда следует, что величина 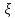должна совершать незатухающие гармонические колебания с круговой частотой :

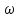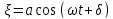
Следовательно:

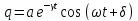
Кривая не периодична. Описывает затухающие колебания.

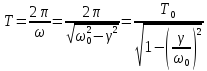-период колебаний.

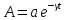-Амплитуда. Она экспоненциально убывает во времени.

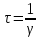
Число полных колебаний, совершаемое за время :

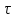Логарифмическим декрементом колебания 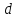называется логарифм отношение амплитуд в моменты последовательных прохождений колеблющейся величины через максимумы или минимумы равно:

,

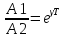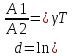
Он связан с число колебаний: 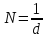, А величина 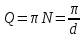–называется Добротностью колебательного контура.

Случай 2: 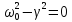Это предельный случай предыдущего, когда период Т обращается в бесконечность. Уравнение 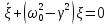переходит в 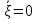 , и , следовательно:

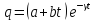
Полагая 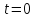, находим Следовательно,

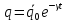
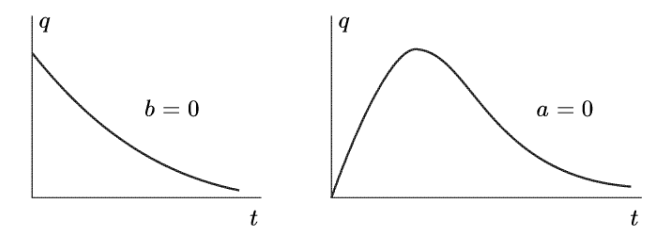
Случай 3: 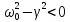, Общее решение будет:

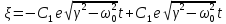
А уравнение (1):

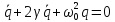
Примет вид:

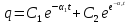
Через 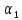и 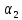обозначенные положительные постоянные:

Если в начальный момент 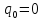, , 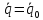то: