2. Порядок выполнения работы:

Детерминированная задача

Модальное управление

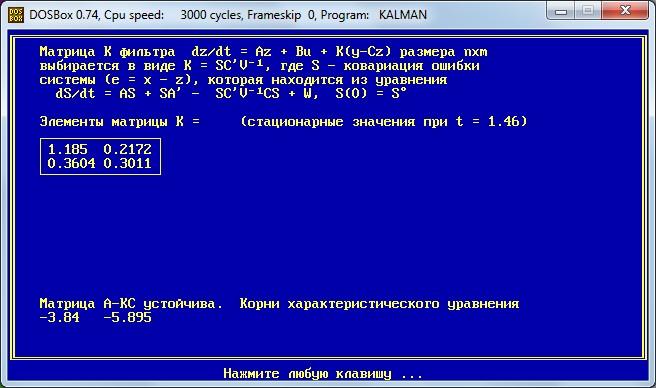
1. Задаем размеры и элементы матрицы А. Определяем корни характеристического уравнения. По виду корней характеристического уравнения сразу можно судить об устойчивости систем регулирования.

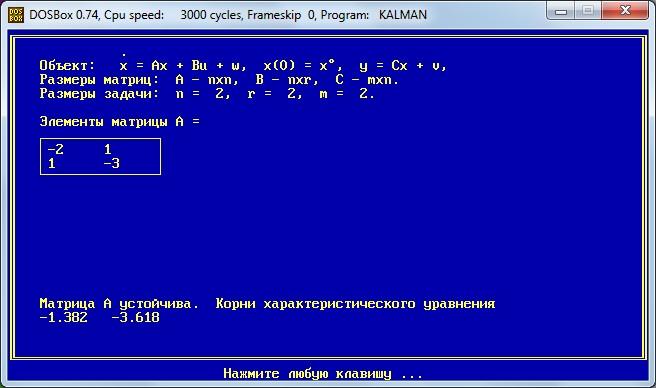
2. Задаем размеры и элементы матрицы В

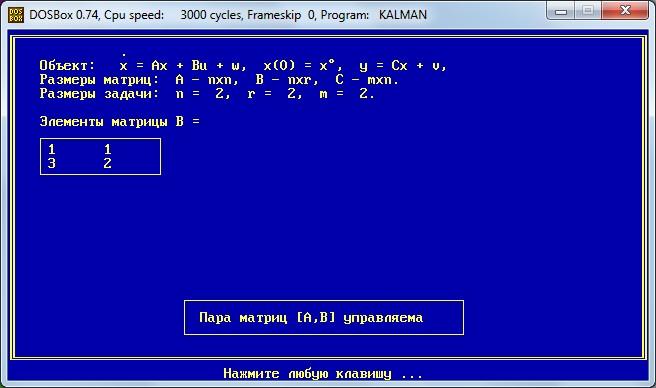
3. Задаем размеры и элементы матрицы С

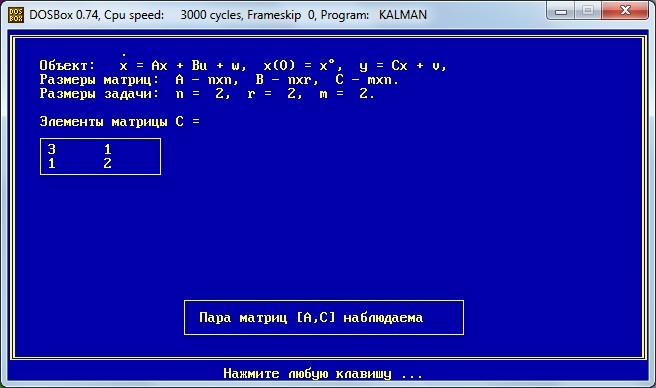
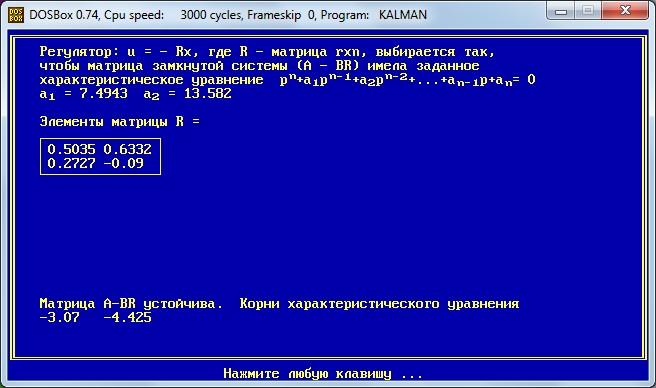
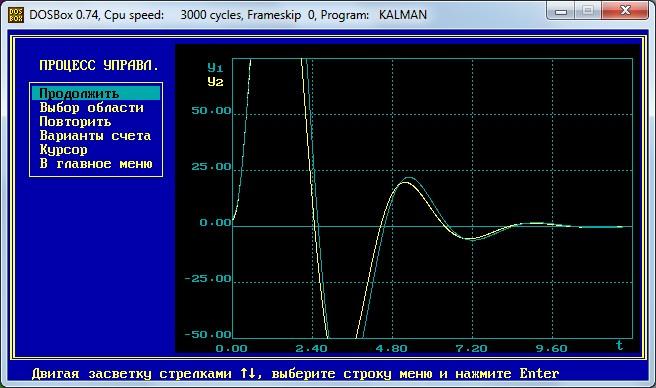
4. Строим переходные процессы для определения устойчивости систем автоматического регулирования и прямых показателей качества работы системы.

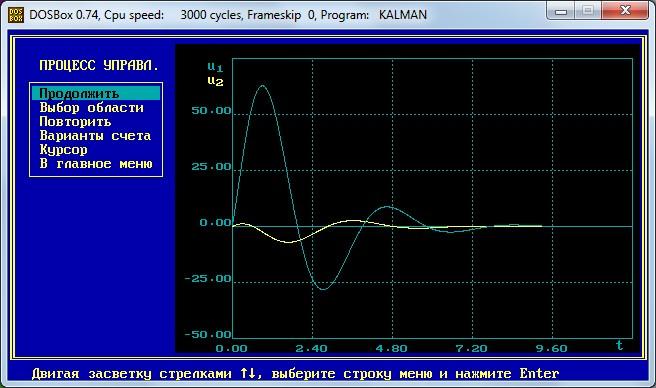
Детерминированная задача

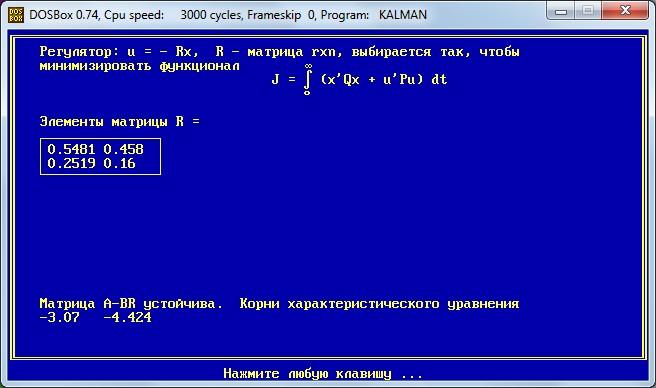
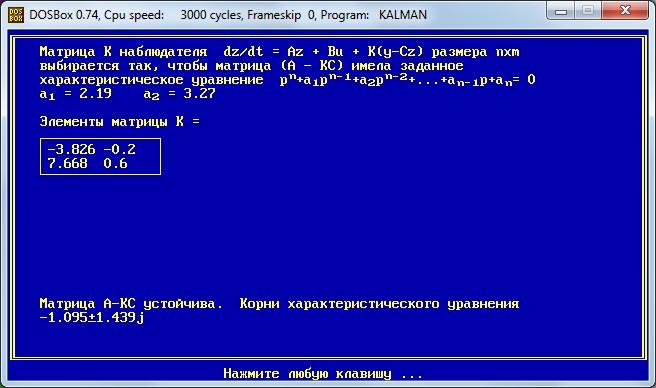
Оптимальное управление

1. Задаём элементы матриц

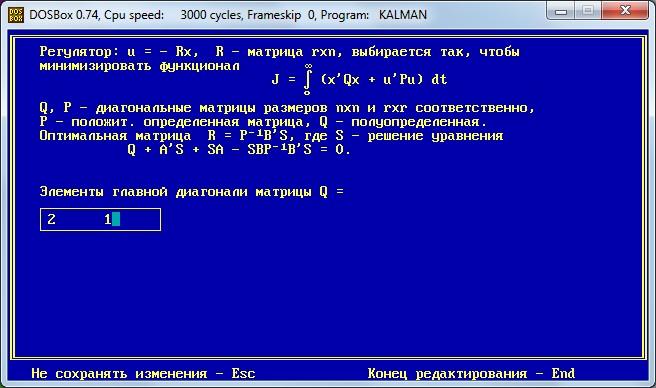
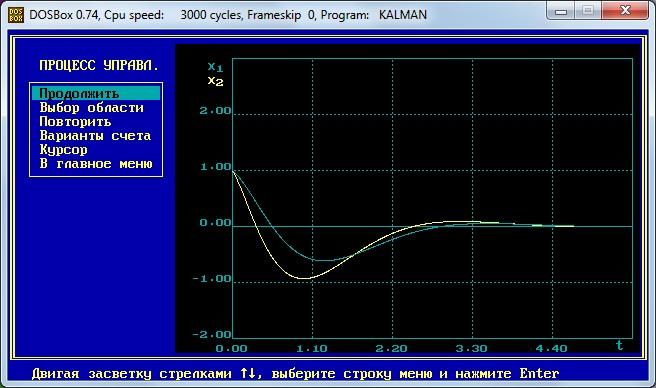
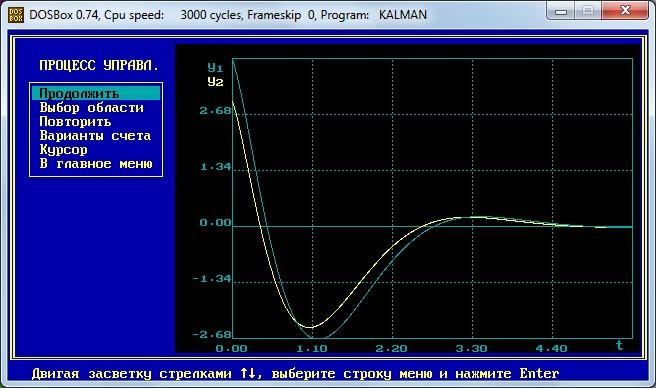
2. Строим переходные процессы в системе

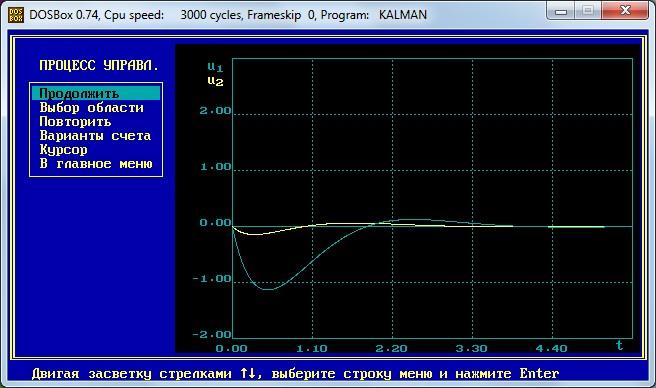
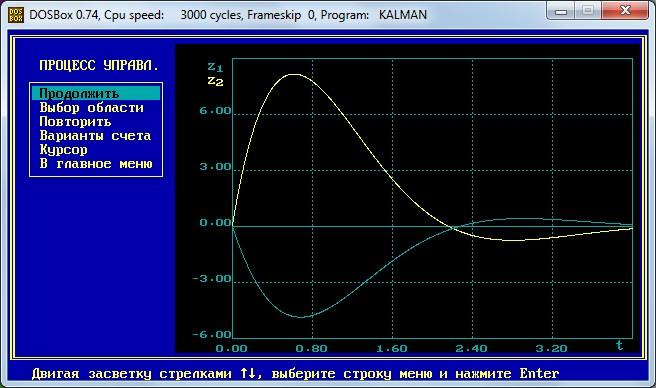
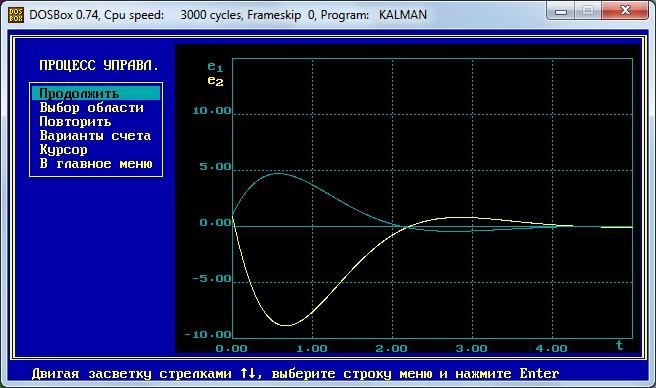
3. Содержание отчета

Отчет должен содержать следующие результаты работы:

1. Структурная схема и передаточная функция объекта регулирования;

2. Коэффициенты характеристического уравнения и передаточной функции;

3. Графики переходных процессов

4. Фазовые траектории, соответствующие устойчивым системам регулирования.

Лабораторная работа №4.

Управление в пространстве состояний при неполной информации. Стохастические задачи

Цель: Ознакомиться с порядком работы Файла kalman.exe.Пакет предназначен для решения задач синтеза линейной системы стабилизации в пространстве состояний.

Оборудование: компьютерный класс с установленным программным комплексом TAY

1. Теоретическая часть:

При запуске пакета на экране появляется «титульный лист» с названием, затем структурная схема системы управления.

В задаче детерминированного управления векторы v и w принимаются равными нулю.

При решении практических задач управления методами пространства состояния часто встречаются случаи, когда не все переменные состояния оказываются измеряемыми. Это обычно имеет место в объектах с распределенными параметрами, в сложных объектах управления и так далее.

Для того, чтобы воспользоваться теорией пространства состояния для управления этими объектами, необходимо оценивать неизмеряемые переменные состояния объекта по его измеряемым входам и выходам.

Задачи, в которых мы не знаем или не можем непосредственно измерить все компоненты вектора состояния, относятся к категории задач управления при неполной информации. Различают при этом детерминированные и статистические методы оценивания вектора состояния.

Рассмотрим синтез детерминированного наблюдателя состояния системы полного порядка, который, по измерениям входных и выходных переменных объекта восстанавливает вектор состояния объекта (полностью все n- компонент).

Допустим, ОУ описывается системой уравнений:

x[k+1]=Фx[k]+Hu[k];

y[k]=cx[k] (1)

У объекта выходов, n- порядок объекта.

Предполагается, что выходные переменные объекта линейно независимы, так что ранг матрицы С равен p.

Идея синтеза наблюдающего устройства, предложенного Луенбергером, основывается на предположении, что матрицы Ф, H и С в уравнении (1) известны, так что объект, модель которого является частью наблюдателя, может быть промоделирован. На модели объекта мы измеряем оценку вектора состояния и находим вектор:

u[k]=-K,

где K - матрица регулятора, с помощью которого мы воздействуем как на реальный объект, так и на модель.

Наблюдатель описывается уравнением:

(2)

Задача заключается в нахождении таких матриц Ф_Н, Н_Н, F_H, при которыхасимптотически стремится к x[k].

Вычитая уравнение (2) из уравнения (1), мы получим вектор ошибки оценивания состояния:

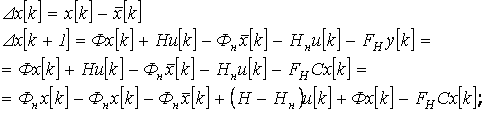
(3)

Для того, чтобы вектор ошибки оценки асимптотически стремился к нулю, должны выполняться следующие три условия:

Ф_Н =Ф-F_HC;

H_H=H;

=( Ф-F_HC) (4)

Система, описываемая последним уравнением, должна быть устойчивой системой. Следует отметить, что при выполнении условия H_H=H вектор ошибкинеуправляем, то есть управляющие воздействия не могут воздействовать на его величину.

Матрица F_H системы выбирается так, чтобы корни характеристического уравнения удовлетворяли условию:

,

при этом система (4) является устойчивой, и вектор ошибкистремится к нулю при.

После подстановки выражений (4) в уравнение (2) получим уравнение наблюдателя:

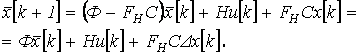(5)

Можно заметить, что наблюдатель представляет из себя модель объекта, на которую воздействует вектор ошибки. Соответствующая блок-схема показана на рис.1.

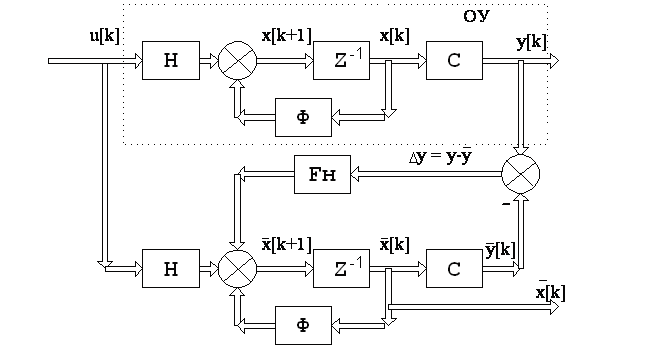
Рис.1.

Помимо рассмотренного наблюдателя полного порядка (n) существуют еще так называемые редуцированные наблюдатели (пониженного порядка), которые не восстанавливают измеряемые компоненты вектора состояния x.

Получим основные соотношения для расчета параметров наблюдателя полного порядка. Итак, в случае выбора параметров наблюдателя в соответствии с рассмотренной выше методикой:

Ф_Н=Ф-F_HC;

H_H=H.

характеристический полином наблюдателя будет иметь вид:

(6)

Для определения параметров наблюдателя поступим аналогично синтезу регулятора, т.е. сначала преобразуем уравнение наблюдателя к канонической форме восстанавливаемости:

(7)

(8)

Преобразование к канонической форме восстанавливаемости:

.

Введем обозначения:

(9)

(10)

Каноническая форма записи матрицы С имеет вид:

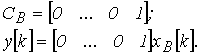
Окончательное уравнение наблюдателя в канонической форме восстанавливаемости будет иметь вид:

(11)

Характеристическое уравнение наблюдателя:

(а₀+f_HB1)+(a₁+f_HB2)z+...+(a_n-1+f_HBn)z^n-1+zⁿ=0

Сравнивая коэффициенты этого уравнения с коэффициентами желаемого характеристического уравнения (6), определяем параметры наблюдателя:

f_HBi=.

Коэффициент наблюдаемости в естественном базисе (исходном):

F_H=QF_HB.

матрица преобразования исходной системы уравнений к канонической форме восстанавливаемости.

Алгоритмы преобразования матрицы к каноническим формам подробно изложены в книгах по матричному счислению и хорошо реализуются на ЭВМ.