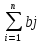Математические методы / Лекции / Лекция №8

Лекция №8

Тема: «Линейное программирование методом потенциалов. Транспортная задача как типовая задача линейного программирования»

Вернемся к ранее рассмотренной транспортной задаче.

Имеется «m» поставщиков какого-либо товара – «A1, A2…Am» и «n» пунктов потребителей этого товара. – «B1, B2..Bn». Обозначим через а_і количество груза (скажем в тоннах или штуках) сосредоточенное или производимое в пунктах Ai (i=1,2..m), а через – количество груза, затребованное в пункте Bj (j=1,2..n).

Тогда можно записать в общем виде, что

a1+a2+..+a_m=b1+b2+..b_n

Означающее, что суммарный запас товара равен суммарной потребности в нем.

В этих задачах помимо чисел и задаются еще величины – стоимость перевозки одной единицы из пункта Ai в пункт Aj.

Требуется определить оптимальный план перевозок, т.е. рассчитать сколько груза должно быть доставлено и сколько отправлено из каждого пункта отправления в каждый пункт назначения при минимальных транспортных затратах.

Итак неизвестными в этой задаче являются «m*n» неотрицательных чисел, где – x_ij (i=1,2..m; j=1,2..n) количество груза, предназначенное для отправки из Ai в Bj. Сведем их в таблицу №1, которая называется «матрицей перевозок». Так как суммарный вес груза, отправленного через а1 во все пункты потребления должен равняться «», то имеем соотношение,

Х11+х12+..+х1n=a1

Аналогичные соотношения должны выполняться для пунктов A2, A3..Am. Следовательно, неизвестные нашей задачи должны удовлетворять m уравнениям

(2)

X11+x12+..x1n=a1

X21+x22+…+x2n=a2

xmn+xm2+..xmn=am

Таблица 1

Пункт назначения Пункт отправления	B1B1	B1B2	--------	BBn	Груз для отправки
Из А1	X11	X12	----------	X1n	а1
Из А2	X21	X22	----------	X2n	а2
---------	-------------	------------	----------	--------
Из Аm	Xm1	Xm2	----------	Xmn	Аm
Востребованные	b1	b2	---------	bn	=

Общее количество груза отправленное из пунктов отправления равно b1

X11+x21+…+xm1=b1

Аналогичное соотношения должны выполняться для всех остальных пунктов, т. е. B2, B3..Bn. Это приводит к n уравнениям:

X11+x21+…+xm1=b1+x12+x22+..+xm2=b2

X1n+x2n+…+xmn=bn

Заметим, что уравнения 2 и 3 очень легко запомнить. В самом деле, уравнение 2 означает, что сумма неизвестных в i–ой строке матрицы перевозок равна a_i; по этой причине будем называть уравнения системы горизонтальными. Аналогично в j-м уравнении системы записан тот факт, что сумма неизвестных j-ого столбца равна; вследствие этого будем называть уравнения системы – вертикальными.

Из пункта Ai в пункт Bj отправляется товар xij при этом стоимость перевозки единицы товара равна Cij. Следовательно перевозка из Ai стоит Cij*Xij, а общая стоимость всех перевозок будет стоить m, n:

S=

Где суммирование производится по всем i- столбцам и j-строкам.

Таким образом, транспортная задача может быть сформулирована следующим образом:

Дана система уравнений 2 и 3, а также целевая функция 4.

Требуется среди неотрицательных решений системы найти такие, которые минимизируют целевую функцию 4. Как и любая задача линейного программирования может быть решена на основе Симплекс-метода с учетом особенностей транспортной задачи.

Система ограничений в виде системы уравнений 2 и 3. Общая процедура симплекс-метода в приложении к транспортной задаче сильно упрощается. Мы изложим очередной метод решения транспортной задачи, который носит название «метод потенциалов». Этот метод представляет собой вариант симплекс-метода, приспособленный специально для решения транспортных задач.

2. Отыскание первого базиса транспортной задачи

Работе по симплекс-методу предшествует подготовительный этап – отыскание первого базиса. Для транспортной задачи имеется простой и надежный метод отыскания первого базиса, который называется «методом северо-западного угла». Прежде чем перейти к его описанию, установим следующий факт: систему 2 и 3 можно разрешить относительно m+n-1 неизвестных.

Действительно, число уравнений в системе 2 и 3 равно «m+n».

Разрешим каждое горизонтальное уравнение кроме первого, относительно неизвестного, стоящего в первом столбце матрицы перевозок:

Xi,j=ai-x12-…-xin, i=2..m (1)

Аналогично каждое вертикальное уравнение, кроме первого разрешим относительно неизвестного xij, стоящего в первой строке матрицы перевозок:

X1,j=bj-x2j-…-xmj, j=2..n,

Остаются еще два уравнения – горизонтальное и первое вертикальное:

X11+x12+…x1n=a1

X11+x21+..xm1=b1

Оба уравнения разрешимы относительно.

X11=a1-x12+…+x1n;

X11=b1-x21-…-xm1

Если вместо неизвестных, входящих в правые части последних двух уравнений поставить выражение 1 и 2, то в результате получаем два выражения для x11:

X11=a1-(b2-x22-…-xm2)-…-(bn-x2n-…-xmn)= a1-b2-…-bn-;

И второе выражение:

X11=b1-(a2-x22-…-x2n)-…-(am-xm2-..-xmn)= b1-a2-…am-

Но ввиду того, что условие 1 имеем:

A1-b2-…-bn=b1-a2-…-am

Следовательно два полученных уравнения для совпадают. Поэтому система (2) и( 3) разрешима относительно неизвестных, стоящих в первой строке, в первом столбце матрицы перевозок. Число этих неизвестных равно ‘m+n+1”.

3. Метод северо-западного угла для отыскания первого базиса

Сущность метода рассмотрим на конкретном примере.

Пусть заданы и четыре пункта назначения. Причем запасы и потребности равны следующим величинам:

А1=60; А2=80; а3=100; b1=40; b2=60; b3=80; b4=60. Сведем эти данные в таблицу 2.

Таблица 2.

Поставка/Отправка	В1	В2	В3	В4	Возможности
А1	40				60
А2					80
А3					100
Потребитель	40	60	80	60	240

Попытаемся удовлетворить потребности первого пункта назначения В1 запасами первого пункта отправления А1. В данном случае, это можно сделать, так как запасы а1=60, превосходят потребности b1=40. Потребности пункта В1 в количестве b1=40 будут удовлетворены полностью и поэтому столбец соответствующий В1 можно исключить из таблицы. Теперь можно считать, что мы пришли к новой таблице 3, в которой три пункта назначения: В2, В3, В4 и три пункта отправления А1, А2, А3. При этом запасы в пункте А1 уменьшились и равны а1=60-40=20.

Отметим, что и в таблице 3 сумма всех потребностей равна сумме всех запасов по прежнему.

К таблице 3 применим тот же прием и попытаемся удовлетворить потребности В2 в количестве b2=60.

(в таблице 3 пункт В2 играет роль первого) запасами а1=20 пункта А1. Очевидно, так как b2>a1.

Впишем в клетку х12 число 20 – это максимум того, что можно перевезти из А1 в В2. При этом потребности В2 сократятся до b1=40, а запасы А1 окажутся исчерпанными полностью. В силу этого, строку, отвечающую А1, из таблицы 3 можно временно удалить. Таким образом, приходим к таблице 4, в которой уже два пункта отправления А2 и А3 и три пункта назначения В2, В3, В4.

Аналогичным приемом продолжаем последовательно сокращать получаемые таблицы, пока не удовлетворим потребности всех пунктов назначения. В силу условия задачи, при этом окажутся исчерпанными все запасы в пунктах отправления.

В процессе сокращения таблиц мы получим следующие значения для некоторых неизвестных:

Х11=40; х12=20; х22=40; х23=40; х33=40; х34=60.

Вписав эти значения в таблицу 2 получим таблицу 5.

ТАБЛИЦА 3						ТАБЛИЦА 4						ТАБЛИЦА 5
	B2	B3	B4		I		B2	B3	B4				B1	B2	B3	B4
A1				20	A2					80	A1		40	20
A2				80	A3					100	A2			40	40
A3				100			40	80	60		A3				40	60
	60	80	60										40	60	80	60	240

Условимся называть те клетки таблицы 5, в которых вписаны значения неизвестных, - базисными, а остальные – свободными.

Если считать, что значения неизвестных Xij, которые отвечают свободным клеткам, равны 0, то получившийся набор значений всех неизвестных дает допустимое решение нашей задачи.

Действительно, проверка показывает, что сумма значений неизвестных в каждой строке таблицы равна запасу в соответствующем пункте отправления, а в каждом столбце – в соответствующем пункте назначения. Поэтому уравнения 2 и 3 удовлетворяются. Теперь остается заметить, что значения всех неизвестных – неотрицательны.

В общем случае, при любом числе пунктов m отправления и любом числе пунктов n назначения, описанный нами метод позволяет заполнитьm+n-1 клетку таблицы.

Действительно, при каждом шаге заполняется только одна клетка. После чего может вычеркиваться одна строка или один столбец таблицы; исключение составляет только последний шаг, когда таблица состоит из одной клетки и, заполнив ее, мы исключаем сразу и строку и столбец.

Так как числовых строк равно m, число всех столбцов n, то число шагов равно m+n-1, т.е. числу базисных клеток.

Покажем, что систему ограничений 2 и 3 можно разрешить относительно неизвестных, отвечающим базисным клеткам. Отсюда следует, что эти неизвестные можно принять за базисные, а остальные клетки как места для небазисных, т.е. свободных неизвестных.

Для доказательства соединим базисные ломаной кривой в том порядке в каком они возникают в рассмотренном примере, что показано на схеме.

Х11	Х12	Х13	Х14
Х21	Х22	Х23	Х24
Х31	Х32	Х33	Х34

Теперь нетрудно видеть, что неизвестные стоящие в базисных клетках могут быть выражены через неизвестные, стоящие в свободных клетках. Эти выражения находятся последовательно: для х11 – из первого вертикального уравнения, затем для

Х12 – из первого горизонтального уравнения

Для х22 – из второго вертикального уравнения

Для х23 – из второго горизонтального уравнения

Для х33 – из третьего вертикального уравнения

Для х34 – из третьего вертикального уравнения или четвертого вертикального уравнения.

Таким образом набор переменных следующий:

Х11, х12, х22, х23, х32, х34.

Этим поставленная задача полностью не решена, так как следовало бы найти выражения для базисных неизвестных через свободные.

Но для дальнейшей работы по решению транспортной задачи методом потенциалов эти уравнения в явном виде не понадобятся и мы их выписывать не будем.

4. Метод потенциалов для решения транспортной задачи

После отыскания первого базиса все переменные уравнения разделяются на две группы:

Xkl- базисные и Xpq – свободные.

Что касается целевой функции «Ф» (общая стоимость всех перевозок), то ее выражение через свободные неизвестные нужно знать обязательно. Другими словами необходимо представить функцию в следующем виде:

Ф=

Покажем как найти коэффициенты Фpq при свободных неизвестных. Сопоставим каждому пункту отправления Аi некоторую величину α_i(i=1,2..m)– «потенциал» пункта Аi. Аналогично каждому пункту назначения Вj сопоставим величину β_j(j=1,2..n) – потенциал пункта Вj.

Свяжем эти величины между собой следующим образом - для каждой базисной неизвестной X_kl составим уравнения:

(2) αk+βl=C_kl;

Где C_kl – стоимость перевозки одной тонны груза из пункта Аk в пункт Вl.

Совокупность уравнений вида (2), составленных для всех базисных неизвестных Хkl образует систему линейных уравнений. В этой системе m+n-1 и m+n неизвестных α_k β_l, (столько сколько имеется пунктов отправления и назначения, вместе взятых).

Покажем, что эта система всегда совместима, причем значение одного из неизвестных можно задать произвольно и тогда значения остальных неизвестных находятся из системы однозначно.

Зафиксируем какое-либо одно решение (α1, α2, αm, β1, β2, βn) системы уравнений (2), в затем для каждого свободного неизвестного вычислим сумму.

Обозначим эту сумму через C’pq :

αp+βq=C’pq

и назовем ее косвенной стоимостью(в отличие от настоящей стоимости Cpq).

Тогда оказывается, что в интересующем нас выражении (1) коэффициенты при свободных неизвестных равны:

Фpq=Cpq-C’pq

Если все величины неотрицательны, то исходное базисное решение будет оптимальным. Если же среди них имеются отрицательные величины(допустим), то мы должны перейти к новому базисному решению.

Этот переход начинается со следующего рассуждения. Будем увеличивать (оставляя другие свободные неизвестные равными нулю). Если при этом наступит такой момент, что одна из базисных неизвестных(допустим обратится в нуль), то мы переходим к новому базису, исключая из старого базиса неизвестное и вводя вместо него. Переходом к новому базису завершается шаг симплекс-метода.

Рассмотрим эти процедуры на примере.

Пример: Даны три пункта отправления А1, А2, А3; с запасами а1=60; а2=80; а3=100. И четыре пункта назначения В1, В2, В3, В4 с потребностями b1=40; b2=60; b3=80; b4=60.

Величина С ij – стоимость перевозки одной тонны груза из Ai в Bj показаны в таблицу 6.

1	2	3	4
4	3	2	0
0	2	2	1

Решение задачи

Начинаем с отыскания первого базиса методом северо-западного угла, который ранее рассматривался. Результаты решения сведены в таблицу 7.

Таблица 7.

40	20
	40	40
		40	60

Обозначим это решение сокращенно Х. Значение целевой функции Ф равняется

Ф==1*40+2*20+3*0+4*0+4*0+3*40+2*40+0*0+2*0+2*40+1*60=420;

Для нахождения потенциалов решим следующую систему уравнений.

α1+β1=C11=1

α1+β2=C12=2

α2+β2=C22=3

α2+β3=C23=2

α3+β3=C33=2

α3+β4=C34=1

Полагая, получим

α=1; β1=0; β2=1; α2=2; β3=0; ; α3=2; β4= -1.

Далее вычисляем косвенные стоимости для свободных неизвестных.

С'13=α1+β3=1'

С'14=α1+β4=0'

С'21=α2+β1=2'

С'24=α2+β4=1'

С'31=α3+β1=2'

С'32=α3+β2=3'

Посчитаем теперь разности. В данном случае,

Фpq=Cpq-C’pq;

Ф13=3-1'=2;

Ф14=4-0'=4;

Ф21=4-2'=2;

Ф24=0-1'=-1;

Ф31=0-2'=-2

Ф32=2-3'=-1.

Таким образом целевая функция Фⁿ равна

S=420+2x₁₃+4x₁₄+2x₂₁-2x₃₁-x₃₂-2x₂₄

Среди коэффициентов неизвестных есть отрицательных (Х24, Х31, Х32). Следовательно можно попытаться уменьшить значение целевой функции. Будем увеличивать, например, величину Х31 (при сохранении остальных).

Свободные неизвестные равные 0. Положим Х31=ρ. Поскольку сумма значений неизвестных в столбцах и строках должна оставаться неизменной, то увеличивая или уменьшая соответствующие значения в базисных клетках.

Таблиця 11

Видно что, ρ=40

40-ρ	20+ρ
	40-ρ	40+ρ
(С13)→ρ		40-ρ	60

Новое решение будет

0	60
		80
40			60

Х →

С13

Целевая функция Ф равна Ф=420-2*40=340

0	60
		80-ρ
40			60-ρ

0	60
		20	60
40		60

Ф=30-1*60=280.