Конспект лекций Высшая математика (Басканова)

872

РАЗДЕЛ 8. ТЕОРИЯ ВЕРОЯТНОСТИ И МАТЕМАТИЧЕСКАЯ

СТАТИСТИКА.................................................................................

874

ЛЕКЦИЯ 8.1. ЭЛЕМЕНТЫ КОМБИНАТОРИКИ. ПОНЯТИЕ ПЕРЕСТАНОВОК, РАЗМЕЩЕНИЙ, СОЧЕТАНИЙ И ПОДСЧЕТ ИХ

ЧИСЛА. ПРАВИЛА СЛОЖЕНИЯ И УМНОЖЕНИЯ........................	874
8.1.1. Комбинаторика...............................................................................	874

ЛЕКЦИЯ 8.2. АЛГЕБРА СОБЫТИЙ. ПРОСТРАНСТВО

ЭЛЕМЕНТАРНЫХ СОБЫТИЙ...............................................................	879
8.2.1. Алгебра событий.............................................................................	879

ЛЕКЦИЯ 8.3. КЛАССИЧЕСКАЯ, ГЕОМЕТРИЧЕСКАЯ И

СТАТИСТИЧЕСКАЯ ВЕРОЯТНОСТЬ.................................................	883
8.3.1. Вероятность события.....................................................................	883
8.3.1.1. Аксиоматическое определение вероятности..........................	883
8.3.1.2. Классическое определение вероятности.................................	883
8.3.1.3. Статистическое определение вероятности.............................	885
8.3.1.4. Геометрическое определение вероятности.............................	885

ЛЕКЦИЯ 8.4. ТЕОРЕМЫ СЛОЖЕНИЯ И УМНОЖЕНИЯ ВЕРОЯТНОСТЕЙ. УСЛОВНАЯ ВЕРОЯТНОСТЬ. ПОЛНАЯ

ВЕРОЯТНОСТЬ И ФОРМУЛА БАЙЕСА.............................................	889
8.4.1. Основные теоремы теории вероятностей..................................	889
8.4.2. Формулы полной вероятности и вероятности гипотез...........	893
8.4.3. Формула Бернулли.........................................................................	484
8.4.4. Приближенные формулы в схеме Бернулли ............................	486

ЛЕКЦИЯ 8.5. ДИСКРЕТНЫЕ И НЕПРЕРЫВНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ. ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ СЛУЧАЙНЫХ ВЕЛИЧИН. ЗАКОНЫ РАСПРЕДЕЛЕНИЯ СЛУЧАЙНЫХ ВЕЛИЧИН.ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ ТЕОРИИ ВЕРОЯТНОСТИ.

СИСТЕМА ДВУХ СЛУЧАЙНЫХ ВЕЛИЧИН .....................................	491
8.5.1. Случайные величины. Способы задания..................................	491
8.5.1.1. Определение случайные величины.........................................	491
8.5.1.2. Способы задания дискретной случайной величины............	492
8.5.1.3. Способы задания непрерывной случайной величины........	494
8.5.2. Числовые характеристики случайных величин......................	495
8.5.3. Моменты...........................................................................................	498
8.5.4. Законы распределения случайных величин.............................	499
8.5.4.1. Законы распределения дискретных случайных величин...	499
8.5.4.1.1. Биноминальное распределение .............................................	499
8.5.4.1.2. Распределение Пуассона .........................................................	500

8.5.4.2. Законы распределения непрерывных случайных величин500

8.5.4.2.1. Равномерное распределение...................................................	500
8.5.4.2.2. Показательное распределение...............................................	502
8.5.4.2.3. Нормальный закон распределения.......................................	504

873
8.5.5. Предельные теоремы теории вероятностей..............................	506
8.5.6. Система двух случайных величин..............................................	507

ЛЕКЦИЯ 8.6. ЗАДАЧИ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ. ГЕНЕРАЛЬНАЯ И ВЫБОРОЧНАЯ СОВОКУПНОСТИ. РЕПРЕЗЕНТАТИВНАЯ ВЫБОРКА. ЭМПИРИЧЕСКАЯ ФУНКЦИЯ

РАСПРЕДЕЛЕНИЯ. ПОЛИГОН И ГИСТОГРАММА.......................	511
8.6.1.Основные задачи математической статистики.........................	511
8.6.2.Генеральная и выборочная совокупности.................................	511

8.6.3.Статистический ряд. Эмпирическая функция распределения

...................................................................................................................... 512

8.6.4.Полигон частот. Гистограмма......................................................

513

ЛЕКЦИЯ 8.7. ТОЧЕЧНЫЕ ОЦЕНКИ ПАРАМЕТРОВ РАСПРЕДЕЛЕНИЯ. НЕСМЕЩЕННОСТЬ, СОСТОЯТЕЛЬНОСТЬ И

ЭФФЕКТИВНОСТЬ ОЦЕНКИ................................................................	516
8.7.1.Статистические оценки..................................................................	516
8.7.2.Точечные оценки.............................................................................	517
8.7.3.Интервальные оценки....................................................................	518

8.7.4.Доверительный интервал для оценки математического

ожидания и дисперсии нормального распределения........................

519

ЛЕКЦИЯ 8.8. КОРРЕЛЯЦИОННЫЙ И РЕГРЕССИОННЫЙ

АНАЛИЗ. ПРОВЕРКА СТАТИСТИЧЕСКИХ ГИПОТЕЗ..................	522
8.8.1.Элементы корреляционного анализа..........................................	522
8.8.2.Регрессионный анализ....................................................................	524
8.8.3.Проверка статистических гипотез...............................................	527

8.8.4.Проверка	гипотезы	о	распределении	генеральной
совокупности. Критерий Пирсона			........................................................	529

КОНТРОЛЬНЫЕ ВОПРОСЫ И ЗАДАНИЯ ДЛЯ САМОПРОВЕРКИ

......................................................................................................................... 531

874

РАЗДЕЛ 8. ТЕОРИЯ ВЕРОЯТНОСТИ И МАТЕМАТИЧЕСКАЯ СТАТИСТИКА

ЛЕКЦИЯ 8.1. ЭЛЕМЕНТЫ КОМБИНАТОРИКИ. ПОНЯТИЕ ПЕРЕСТАНОВОК, РАЗМЕЩЕНИЙ, СОЧЕТАНИЙ И ПОДСЧЕТ ИХ ЧИСЛА. ПРАВИЛА СЛОЖЕНИЯ И УМНОЖЕНИЯ

8.1.1. Комбинаторика

Комбинаторика (комбинаторный анализ) – раздел дискретной математики, посвященный решению задач выбора и расположения элементов некоторого, обычно конечного, множества в соответствии с заданными правилами. Например, сколькими способами можно выбрать 6 карт из колоды, состоящей из 36 карт; или сколькими способами можно составить очередь, состоящей из10 человек и т.д. Каждое правило в комбинаторике определяет способ построения некоторой конструкции, составленной из элементов исходного множества и называемой комбинацией. Основная цель комбинаторики состоит в подсчете количества комбинаций, которые можно составить из элементов исходного множества в соответствии с заданным правилом. Простейшими примерами комбинаторных конструкций являются перестановки, размещения и сочетания.

Рождение комбинаторики связано с работами Б. Паскаля и П. Ферма по поводу азартных игр, большой вклад внесли Лейбниц, Бернулли, Эйлер. В настоящее время интерес к комбинаторике связан с развитием компьютеров. Нас в комбинаторике будет интересовать возможность определения количественно различных подмножеств конечных множеств, для вычисления вероятности классическим способом.

Для определения мощности множества, которые соответствуют тому или иному событию полезно разобраться с двумя правилами комбинаторики: правило произведения и правило суммы (иногда их называют принципами умножения и сложения соответственно).

Правило произведения: пусть из некоторого конечного множества 1-й объект можно выбрать k1 способами,

2-ой объект – k2 способами,

………………………………

n-ый объект kn способами.	(8.1.1)
Тогда произвольный набор, перечисленных n	объектов, из данного

множества можно выбрать k1, k2, …,kn способами.

Пример 1. Сколько существует трехзначных чисел с разными цифра-

ми?

Решение. В десятичной системе исчисления десять цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. На первом месте может стоять любая из девяти цифр (кроме нуля).

875

На втором месте – любая из оставшихся 9 цифр, кроме выбранной. На последнем месте любая из оставшихся 8 цифр.

По правилу произведения, 9·9·8 = 648 трёхзначных чисел имеют разные цифры.

Пример 2. Из пункта A в пункт B ведут 3 дороги, а из пункта B в пункт C

– 4 дороги. Сколькими способами можно совершить поездку из A в C через B? Решение. В пункте A есть 3 способа выбора дороги в пункт B, а в пункте B есть 4 способа попасть в пункт C. Согласно принципу умножения, суще-

ствует 3 4=12 способов попасть из пункта A в пункт C.

Правило суммы: при выполнении условий (8.1.1), любой из объектов можно выбрать k1+k2+…+kn способами.

Пример 3. Сколько существует способов выбора одного карандаша из коробки, содержащей 5 красных, 7 синих, 3 зеленых карандаша.

Решение. Один карандаш, по правилу суммы, можно выбрать 5+7+3=15 способами.

Пример 4. Пусть из города A в город B можно добраться одним авиамаршрутом, двумя железнодорожными маршрутами и тремя автобусными маршрутами. Сколькими способами можно добраться из города A в город

B ?

Решение. Все условия принципа сложения здесь выполнены, поэтому, в соответствии с этим принципом, получим 1+2+3=6 способов.

Рассмотрим пример, иллюстрирующий различие принципов умножения и сложения.

Пример 5. В магазине электроники продаются три марки телевизоров и два вида видеомагнитофонов. У покупателя есть возможности приобрести либо телевизор, либо видеомагнитофон. Сколько способами он может совершить одну покупку? Сколько различных комплектов, содержащих телевизор и магнитофон, можно приобрести в этом магазине, если покупатель собирается приобрести в паре и телевизор, и видеомагнитофон?

Решение. Один телевизор можно выбрать тремя способами, а магнитофон – другими двумя способами. Тогда телевизор или магнитофон можно купить 3+2=5 способов.

Во втором случае один телевизор можно выбрать тремя способами, после этого видеомагнитофон можно выбрать двумя способами. Следовательно, в силу принципа умножения, купить телевизор и видеомагнитофон можно 3 2=6 способами.

Рассмотрим теперь примеры, в которых применяются оба правила комбинаторики: и принцип умножения, и принцип сложения.

Пример 6. В корзине лежат 12 яблок и 10 апельсинов. Ваня выбирает либо яблоко, либо апельсин, после чего Надя выбирает из оставшихся фруктов и яблоко и апельсин. Сколько возможно таких выборов?

876

Решение. Ваня может выбрать яблоко 12 способами, апельсин – 10 способами. Если Ваня выбирает яблоко, то Надя может выбрать яблоко 11 способами, а апельсин – 10 способами. Если Ваня выбирает апельсин, то Надя может выбрать яблоко 12 способами, а апельсин – 9 способами. Таким образом, Ваня и Надя могут сделать свой выбор 12 11 10 10 12 9 2400 спосо-

бов.

Пример 7. Есть 3 письма, каждое из которых можно послать по 6 адресам. Сколькими способами это можно сделать?

Решение. В данной задаче мы должны рассмотреть три случая: а) все письма рассылаются по разным адресам, б) все письма посылаются по одному адресу, в) только два письма посылаются по одному адресу. Если все письма рассылаются по разным адресам, то число таких способов легко на-

ходится из принципа умножения: n1=6 5 4=120 способов. Если все письма посылаются по одному адресу, то таких способов будет n2=6. Таким образом, остается рассмотреть только третий случай, когда только 2 письма посылаются по одному адресу. Выбрать какое-либо письмо мы можем 3 способами, и послать его по какому-либо выбранному адресу можем 6 способами. Оставшиеся два письма мы можем послать по оставшимся адресам 5 способами. Следовательно, послать только два письма по одному адресу мы можем n3=3 6 5=90 способами. Таким образом, разослать 3 письма по 6 адресам в соответствие с принципом сложения можно

n1 n2 n3 120 6 90 216 способами.

Обычно в комбинаторике рассматривается идеализированный эксперимент по выбору наудачу k элементов из n. При этом элементы: а) не возвращаются обратно (схема выбора без возвращений); б) возвращаются обратно (схема выбора с возвращением).

1. Схема выбора без возвращений.

Размещением из n элементов по k называют любой упорядоченный набор из k элементов, принадлежащих n элементному множеству. Различные размещения отличны друг от друга или порядком элементов, или составом.

	Число размещений из n элементов по k обозначается Ak			и вычисляется
	по формуле		n
		n!
	Ak			(8.1.2)
	n	(n k)!

где n!=1 2 3 … n, 1!=1, 0!=1.

Пример 8. В соревнованиях участвует 10 человек, трое из них займут 1, 2, 3 место. Сколько существует различных вариантов?

Решение. В этом случае важен порядок распределения мест. Число различных вариантов равно

				877
A3		10!		7! 8 9 10 8 9 10 720
10		(10 3)!		7!

Перестановкой из n элементов называют размещение из n элементов по n Число перестановок из n элементов обозначают Pn и вычисляют по формуле

P An n!			n!	(8.1.3)
n	n	0!

Пример 9. Сколько существует способов расстановки 10 книг на пол-

ке?

Решение. Общее число способов расстановки определяется как число перестановок (8.1.3) из 10 элементов и равно P10 = 10! =3628 800.

Сочетанием из n элементов по k называется любой набор из k элементов, принадлежащих n элементному множеству. Различные сочетания отличаются друг от друга только составом.

Число сочетаний из n элементов по k обозначается Cnk и вычисляется

	по формуле	Ak
	Cnk			n!
		n				(8.1.4)
		Pk		(n k)!k!

Справедливы тождества:

Cnk Cnn k

Cnk 1 Cnk Cnk 1

Cn0 1

Cn1 n

Пример 10. Сколько существует способов выбора трех человек из де-

сяти.

Решение. В данном случае при выборе для нас важен только состав наборов по три человека, порядок выбора роли не играет, поэтому в отличие от предыдущего примера число способов выбора подсчитаем по формуле соче-

таний (8.1.4)

C3			10!		7! 8 9 10 7! 8 9 10 120
10		(10	3)!3!		7! 3!	7! 1 2 3

2. Схема выбора с возвращениями.

Если при выборе k элементов из n элементы возвращаются обратно и упорядочиваются, то говорят, что это размещения с повторениями.

Число размещений с повторениями:

Ak	nk	(8.1.5)
n

878

Пример 11. В гостинице 10 комнат, каждая из которых может разместить четырех человек. Сколько существует вариантов размещения, прибывших четырех гостей?

Решение. Каждый следующий гость из 4 может быть помещён в любую из 10 комнат, так как рассматривается идеализированный опыт, поэтому общее число размещений, по формуле размещений с повторениями (8.1.5), равно

A104 104 10 000

Если при выборе k элементов из n элементы возвращаются обратно без последующего упорядочивания, то говорят, что это сочетания с повторениями. Число сочетаний с повторениями из n элементов по k определяется по формуле

Cnk k 1

(8.1.6)

Пример 12. В магазине продается 10 видов тортов. Очередной покупатель выбил чек на три торта. Считая, что любой набор товаров равновозможен, определить число возможных заказов.

Решение. Число равновозможных заказов по формуле (8.1.6) равно

C3	3 1	C3			12!		220 .
10		12		(12	3)!3!

879

ЛЕКЦИЯ 8.2. АЛГЕБРА СОБЫТИЙ. ПРОСТРАНСТВО ЭЛЕМЕНТАРНЫХ СОБЫТИЙ

8.2.1. Алгебра событий

Одним из основных понятий теории вероятностей является опыт. Под опытом понимается выполнение комплекса условий, в результате которого происходят или не происходят определенные события (факты).

Простейшие неразложимые результаты опыта называются элементарными событиями (ωi), а вся совокупность элементарных событий называется пространством элементарных событий Ω={ωi}. С каждым опытом связано свое пространство элементарных событий Ω. Например, игральная кость подбрасывается один раз. Элементарные события: 1 – появление 1, 2 – 2,3 – 3, 4 – 4, 5 – 5, 6 – 6. Пространство элементарных событий ={ 1, 2,

3, 4, 5, 6}

Любое конечное или счетное подмножество Ω, называется событием. Различают три типа событий:

1)достоверные, которые всегда произойдут в результате опыта (Ω),

2)случайные, могут либо произойти в результате опыта, либо нет,

3)невозможные, никогда не произойдут в результате опыта (0 или ). События обычно обозначают первыми прописными буквами латинско-

го алфавита: A, B, C,...

События A и B несовместны, если в результате одного опыта они не могут происходить одновременно, в противном случае – совместны. Например, при одном подбрасывании монеты не могут одновременно появиться герб и решка.

Элементы последовательности событий A1, A2,..., An попарно несовместны, если любые два из них несовместны. Например, при подбрасывании игральной кости никакие два элементарные исхода (появление цифр 1, 2, 3, 4, 5, 6) не могут произойти одновременно.

Несколько событий равновозможны, если ни одно из них не имеет объективного преимущества перед другими. Например, элементарные исходы при подбрасывании монеты, игральной кости.

События A1, A2,..., An образуют полную группу, если в результате опыта кроме этих событий ничего не может произойти.

Приведем примеры полных групп событий:

–выигрыш и проигрыш в лотерее для одного лица;

–выпадение «герба» и «цифры» при бросании одной монеты;

–появление числа очков 1, 2, 3, 4, 5, 6 в опыте с игральной костью;

–появление четной или нечетной цифры в том же опыте.

880

Обычно Ω изображают на плоскости в виде некоторой области, а ωi в виде точек этой области, устанавливая, таким образом, соответствие между событиями и точечными множествами.

Над событиями вводятся операции, совпадающие с операциями над множествами: сумма, произведение, отрицание.

Суммой событий A и B называется такое третье событие A+B (или A B ), которое заключается в наступлении хотя бы одного из событий или

A, или B (рис. 8.2.1).

А

В

А

В

События несовместны				События совместны

Рисунок 8.2.1. Сумма событий

Если A и B несовместны, то появление обоих вместе отпадает и сумма сводится к появлению любого из событий, безразлично какого. Можно складывать несколько событий. Разберем это на следующих примерах.

Пример 1. Опыт: вынимают наугад одну карту из колоды. События: A

–появление червонной масти, B – появление бубновой масти. A и B – несовместные события. Сумма событий:

S = A + B – появление красной масти (безразлично какой).

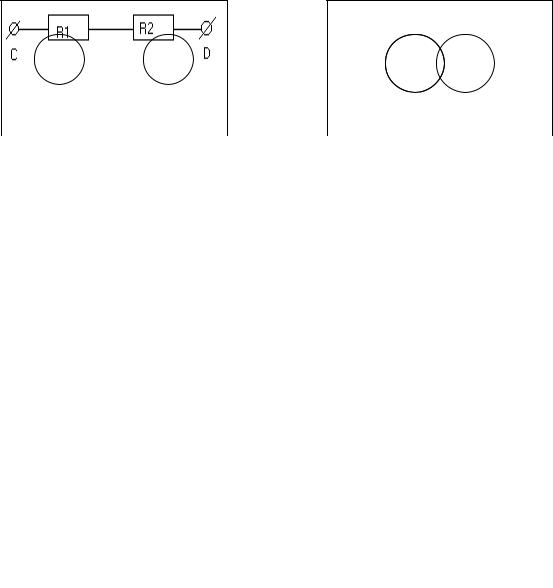
Пример 2. Дана часть электрической цепи (рис. 8.2.2). События: R1 – обрыв первого сопротивления, R2 – обрыв второго сопротивления. S = R1 + R2

–обрыв цепи между точками C и D. В данном случае R1 и R2 – совместные события, поэтому под их суммой подразумевается обрыв хотя бы одного сопротивления (последовательное соединение), т.е. первого или второго, либо обоих вместе.

Рис.8.2.2. Иллюстрация к примеру 2

Пример 3. Опыт: бросают игральную кость. События: A – выпадение цифры 1, B – выпадение цифры 3, C – выпадение цифры 5. A, B, C – несовместные события. S = A + B + C – появление нечетной цифры, т. е. выпадение либо 1, либо 3, либо 5.

881

Пример 4. Опыт: проводят соревнования по футболу, баскетболу и волейболу. События: A – друзья пошли на футбол, B – друзья пошли на баскетбол, C – друзья пошли на волейбол. A, B, C – несовместные события.

S = A + B + C – друзья пошли на соревнования.

Если в условиях данного опыта несколько событий A1, A2,…,An образуют полную группу, то их сумма является достоверным событием.

Произведением двух событий A и B называется такое третье событие A B (или A B ), которое заключается в наступлении событий A и B одновременно. Если события A и B несовместны, то A B= (рис. 8.2.3).

А

В

А

В

События несовместны		События совместны

Рисунок 8.2.3. Произведение событий

Пример 5. Опыт: вынимают наугад одну карту из колоды. События: A

– появление туза, B – появление бубновой масти.

C = A · B – появление бубнового туза. Пример 6. Опыт: бросание трех монет. События:

A1 – выпадение «герба» на первой монете,

B1 – выпадение «решки» на первой монете, A2 – «герб» на второй монете,

B2 – «решка» на второй монете,

A3 – «герб» на третьей монете,

B3 – «решка» на третьей монете.

C =A1·A2 A3 – герб на трех монетах;

C =B1·B2·B3 – решка на трех монетах.

Если события несовместны, то их произведение – невозможное собы-

тие.