ALL

Изображение эллипса методом средней точки

•Далее переходим из области 1 в область 2, поскольку 2ry2 x > 2rx2 y. Для области 2 начальной точкой будет (x0, у0) = (7,3), а начальный параметр принятия решения равен

•p20 = fэллипс (7 + ½, 2) = – 151

•Затем находятся остальные положения пикселей эллипса в первом квадранте.

	•
		k	p1	k	(x	, y	)	2r 2	x	2r 2	y
					k+1	k+1		y	k+1	x	k+1
		0	-151		(8, 2)			576		256
		1	233		(8,1)			576		128
		2	745		(8, 0)			————		———

•График рассчитанных положении пикселей на эллиптической траектории в первом квадранте показан на рис.

•Рис. Положения пикселей на эллиптической траектории с

центром в начале координат и rx = 8 и rу =6. Иллюстрация использования алгоритма средней точки для вычисления положений точек в первом квадранте.

3.3. Алгоритм вывода эллипса

•Инкрементный алгоритм для эллипса подобен алгоритму для круга, но более сложный.

3.3.Алгоритм вывода эллипса

•В этом алгоритме использована симметрия эллипса по квадрантам (рис. 3.5)

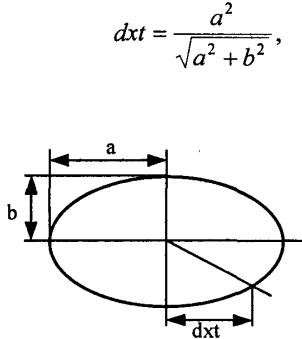
•Алгоритм состоит из двух циклов. Сначала от x = 0 до х = dхt, где

•а потом цикл до точки х = а, у = 0.

•Рис. 3.5. Вывод эллипса

ДРУГИЕ КРИВЫЕ

•При объектном моделировании, описании траекторий в анимации, построении графиков данных и функций, а также в других графических приложениях могут оказаться полезными функции построения различных кривых.

•Чаще всего встречаются такие кривые, как конические сечения, тригонометрические и показательные функции, распределения вероятности, полиномы общего вида и сплайны.

•Изображения этих кривых можно получить с помощью методов, аналогичных применяющимся для изображения окружностей и эллипсов. Координаты точек на кривой можно найти непосредственно из явного выражения функции у = f(х) или из параметрических уравнений. Или же можно воспользоваться методом средней точки с нахождением приростов и построить кривую, которая задается в виде неявной функции f(x, у) = 0.

•Самый простой способ изображения кривой линии — аппроксимировать ее прямолинейными отрезками. В этом случае часто полезны параметрические представления, позволяющие получить на траектории кривой точки (концы отрезков), находящиеся на одинаковом расстоянии друг от друга. Такие точки можно также найти из явного выражения, выбрав независимую переменную в соответствии с тангенсом угла наклона кривой.

•Там, где величина тангенса угла наклона кривой у = f(х) меньше 1, в качестве независимой переменной выбирается х, и через равные промежутки х находятся значения у. Чтобы получить одинаковые интервалы в той области, где величина тангенса угла наклона больше 1, можно воспользоваться обратной функцией, х = f-1(у), и найти значения х через равные интервалы у.

ДРУГИЕ КРИВЫЕ

•Аппроксимация в виде прямой или кривой линии используется также для построения линейного графика набора дискретных значений. Дискретные точки можно соединить прямолинейными отрезками либо воспользоваться методом наименьших квадратов и аппроксимировать набор данных одной прямой линией. Нелинейный метод наименьших квадратов используется при изображении набора данных с помощью некоторой аппроксимирующей функции, обычно в этой роли выступает полином.

•Кроме эллипса или окружности, определенной симметрией обладают многие функции, и этим можно воспользоваться для уменьшения объема вычислений при расчете координат пикселей на кривой. Например, функция нормального распределения вероятности симметрична относительно своего центра (среднего значения), а все точки в пределах одного периода синусоиды можно получить с помощью точек из интервала

90°.

Кривая Безье

•Разработана математиком Пьером Безье. Кривые и поверхности Безье были использованы в 60-х годах компанией "Рено" для компьютерного проектирования формы кузовов автомобилей. В настоящее время они широко используются в компьютерной графике.

•Кривые Безье описываются в параметрической форме:

•х = Px(t)

•y = Ру(t).

•Значение t выступает как параметр, которому отвечают координаты отдельной точки линии. Параметрическая форма описания может быть более удобной для некоторых кривых, чем задание в виде функции у= f(х). Это потому, что функция f(x) может быть намного сложнее, чем Рх(t) и Ру(t), кроме того, f(х) может быть неоднозначной.

•Многочлены Безье для Рх и Ру имеют такой вид:

•где Cmi — сочетание m по i (известное также по биному Ньютона),

•Cmi= m! /(i!( m-i)!), а хi и уi— координаты точек-ориентиров Рi. Значение m можно рассматривать и как степень полинома, и как значение, которое на единицу меньше количества точек-ориентиров.

3.4.Кривая Безье

•Рассмотрим кривые Безье, классифицируя их по значениям m.

•m=1 (по двум точкам).

•Кривая вырождается в отрезок прямой линии,

•определяемый концевыми точками Р0 и Р1,

• как показано на рис. 3.6.					• Рис. 3.6. Кривая Безье (m = 1)
•	Р(t) = (1 – t)P0+tP1.
• m =2 (по трем точкам, рис. 3.7)
•	Р(t) = (1 – t)2P	0	+ 2t(1 - t)Р	1	+ t2Р .
					2
• m =3 (по четырем точкам, кубическая, рис. 3.8).
• Используется довольно часто, в особенности
•	в сплайновых кривых.

• Р(t) = (1 – t)3P0 + 3t(1 - t)2Р1 - 3t(1 - t)2Р2 + t3Р3

• Рис. 3.7. Кривая Безье (m =2)

• Рис. 3.8. Кубические кривые Безье (m = 3)

Геометрический алгоритм для кривой Безье

•Этот алгоритм позволяет вычислить координаты (х, у) точки кривой Безье по значению параметра t. Алгоритм описан в [19].

•1. Каждая сторона контура многоугольника, проходящего по точкам-ориентирам, делится пропорционально значению t.

•2. Точки деления соединяются отрезками прямых и образуют новый многоугольник. Количество узлов нового контура на единицу меньше, чем количество узлов предыдущего контура.

•3. Стороны нового контура снова делятся пропорционально значению t.

•И так далее. Это продолжается до тех пор, пока не будет получена единственная точка деления. Эта точка и будет точкой кривой Безье (рис. 3.9).

•Рис. 3.9. Геометрический алгоритм для кривых Безье

•Приведем запись геометрического алгоритма на языке С++:

•Результат работы алгоритма— координаты одной точки кривой Безье записываются в R[0].

Алгоритмы вывода фигур

•Фигурой здесь будем считать плоский геометрический объект, который состоит из линий контура и точек, которые содержатся внутри контура.

•В общем случае линий контура может быть несколько — когда объект имеет внутри пустоты. В этом случае для описания таких фигур необходимы два и более контуров.

•Рис. Пример фигуры

•В некоторых графических системах одним объектом может считаться и более сложная многоконтурная фигура — совокупность островов с пустотами.

•Графический вывод фигур разделяется на две задачи:

•вывод контура

•и вывод точек заполнения.

•Поскольку контур представляет собой линию, то вывод контура проводится на основе алгоритмов вывода линий. В зависимости от сложности контура, это могут быть отрезки прямых, кривых или произвольная последовательность соседних пикселей.

•Для вывода точек заполнения известны методы, разделяющиеся в зависимости от использования контура на два типа— алгоритмы закрашивания от внутренней точки к границам произвольного контура и алгоритмы, которые используют математическое описание контура.

06. Закрашивание