ALL

ПАРАМЕТРИЧЕСКИЕ КРИВЫЕ

•Стандартная параметрическая форма единичной окружности:

•	x = cosθ, 0 θ 2 ,
•	у = sinθ,
•	или
•	Р(θ) = [х у] = [cosθ sinθ],	0 θ 2 ,

•где параметр θ — геометрический угол, отмеряемый

•против часовой стрелки от положительной полуоси х.

•На рис. 3 сравниваются непараметрическое

•и параметрическое представления окружности

•в первом квадранте.

•Непараметрический вид (рис. 3 а). Точки на дуге соответствуют равным приращениям х. Дуга состоит из отрезков разной длины – получается приблизительное графическое представление окружности. Кроме того, расчет квадратного корня –вычислительно дорогостоящая операция.

•На рис. 3 b изображена дуга, построенная по равным приращениям параметра θ в пределах 0 θ /2. Точки располагаются на одинаковом расстоянии вдоль окружности, и окружность выглядит гораздо лучше. Недостаток такого представления — сложность вычисления тригонометрических функций.

Рис. 3 a

Рис. 3 b

	ПАРАМЕТРИЧЕСКИЕ КРИВЫЕ
• Параметрическом представление кривой не		Рис. 3 с
	единственно, например,
•	0 t 1 (1)

•также представляет дугу единичной окружности в первом квадранте (рис. 3 с).

•На рис. З с показан результат для равных приращений t. Он лучше, чем у явного, но хуже, чем у стандартного параметрического представления. Однако уравнение (1) проще с вычислительной точки зрения, т.е. это компромиссное решение.

•Связь между параметрическим представлением и стандартным параметрическим представлением показана на рис. 4. Из него видно, что для единичной окружности

Рис. 4 Связь между параметрическими представлениями.

Математическое представление прямых линий и отрезков в

машинной графике.

• Прямая

•Описания вида "y=ax+b" не используются в компьютерной графике

•Прямая задается координатами двух точек (начальной и конечной)

•Для описания прямой используется в основном матричное и параметрическое представление.

•Матричное представление:

•Для произвольной точки на отрезке из соотношений

•катетов подобных треугольников получим (z для 3D)

	x x1			y y1			z z1			Рис. 2
	x	x		y	y		z	2	z
	2	1		2	1				1

•Отсюда матричное представление:

•Для плоской прямой используется первое уравнение, а для пространственной используется оба этих уравнения.

•Самое простое параметрическое представление у прямой.

•Для двух векторов положения P1 и Р2 параметрический вид отрезка прямой между

ними :	P2 (x2 , y2 , z2 )
• P(t) =P1 + (P2 – P1)t,	0 < t < 1.

P(x , y , z )

1 1 1 1

Математическое представление прямых линий и отрезков в машинной графике.

•Параметрическое представление

•Так как P(t) это вектор, у каждой его составляющей есть параметрическое представление

x(t) и y(t) между P1	и Р2:	x(t) x1 (x2	x1) t
• x(t) =x1+ (x2 –x1)t,	0<t<1.	y(t) y1 ( y2	y1) t

•y(t) = y + (y - y )t

1(z2 z1) t

•Достоинства:

•Не требует для точек операции деления и в этом случае не получается ситуации переполнения данных при делении на ноль, когда результат получается близким к бесконечности.

•Описание прямой не зависит от положения точек, в этом случае эти уравнения

позволяют создать тестовые функции:	f (x, y) (x x )( y	2	y ) ( y y )(x x )
	1		1	1 2 , 1

используемые для определения положения точек.

–Если функция f(x,y)=0,то точка P3(x3,y3), подставленная в это выражение вместо x и y находится на этой прямой.

–Если f(x,y)> 0, то точка находится справа от прямой, идущей от точки Р1 к точке Р2.

•	P2	P2
•
	P1	P1
–	Если < 0, то точка находится слева от точек Р1 и Р2

•

Математическое представление прямых линий и отрезков в машинной графике.

• Параметрическое представление. Координаты не зависят друг от друга, а каждая координата зависит от дополнительного параметра "t"

• Особенность: x(t) x1 (x2 x1) t

• Если 0 ≤ t ≤1, то описывается отрезок.	y(t) y1	( y2	y1) t
• Если t < 0, то это участок от "– " до точки .	z(t) z1	(z2	z1) t

•Если t > 1, то это участок от точки до "+ .

•Параметрическое описание используется для определения точек пересечения двух прямых. Например, точки для одной прямой задаются в матричной форме, а для второй параметрической форме.

•Если обе прямые заданы в параметрическом виде, в одном случае используют “t”, а во втором “ ”. Если эти переменные лежат в диапазоне от 0 до 1, то прямые пересекаются

		своими отрезками.			x3	(x4	x3 ) x1 (x2 x1 )t
	•	приравняем два уравнения прямых
					y3	( y4	y3 ) y1 ( y2 y1 )t
			(x3 x1 ) (x4 x3 ) (x2 x1 )t
		получим
	•		( y3 y1 ) ( y4 y3 ) ( y2 y1 )t
	•
	умножим уравнения на ( y2 y1 ) и (x2			x1 ) соответственно и вычитаем одно из другого
	• (x3 x1 )( y2 y1 ) (x4 x3 )( y2 y1 )			( y3 y1)(x2 x1) ( y4 y3 )(x2 x1)
	•	Т.е. (x4 x3 )( y2 y1 ) ( y4 y3 )(x2 x1 )					x y x y
	•	Если это условие выполняется, то прямые параллельны.

Математическое представление прямых линий и отрезков в машинной графике.

•С помощью матричного представления можно описать отрезок, перпендикулярный

	данному.
•
•	описание отрезка перпендикулярного заданному отрезку.

•Например, мы хотим построить перпендикулярный отрезок, который проходит через заданную точку Р3, такая прямая задается следующим образом:

•	P2	P3

•	P1

•

•Для того, чтобы перпендикулярная прямая проходила через точку Р2:

•В первом случае перпендикулярная прямая проходит через точку Р1

ПАРАМЕТРИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ ОКРУЖНОСТИ

•Параметрическое представление окружности радиуса r с центром в начале координат:

–	x = rcosθ,	0 θ 2 ,
–	y = rsinθ,	0 θ 2 ,	(2)

•где θ — параметр. Для полной окружности диапазон изменения параметра θ от 0 до 2 .

•Если рассматривать некоторое фиксированное число равномерно распределенных точек по окружности, то приращение параметра ∆θ между точками можно считать константой. Координаты любой точки на окружности с центром в начале координат

–xi+1= rcos(θi + ∆θ),

–yi+1= rsin(θi + ∆θ),

• где θi —значение параметра для точки хi, yi.	∆θ
• По формуле суммы углов

– xi+1= r (cos θi cos ∆θ — sin θi sin ∆θ),

– yi+1= r(cos θi sin ∆θ + cos ∆θ sin θi).

•для θ = θi

–xi = rcosθi,

–yi = rsinθi,

•получим рекурсивные уравнения

–xi+1 = xi cos ∆θ - yi sin ∆θ,

–yi+1 = xi sin ∆θ + yi cos ∆θ,

• что соответствует повороту точки xi, yi на ∆θ.

ПАРАМЕТРИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ ОКРУЖНОСТИ

•Каждую последующую точку вычисляют из предыдущей и какого-нибудь угла ∆θ в итоге получается многоугольник.

•Так как θ постоянно и равно 2 /(n – 1), где n - количество равномерно распределенных по окружности точек, значения sin и cos нужно вычислить только один раз.

•Используются только умножения, вычитание и сложение, поэтому алгоритм работает быстро.

•Окружность с центром в произвольной точке получается переносом окружности соответствующего радиуса с центром в начале координат.

•Можно упростить задачу: сначала строить единичную окружность с центром в начале координат, а затем, комбинируя перенос и масштабирование, получить окружности с любым радиусом и центром.

•Таблица 1 Результаты для единичной окружности

•Результаты для остальных точек в таблице 1.

ПАРАМЕТРИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ ОКРУЖНОСТИ

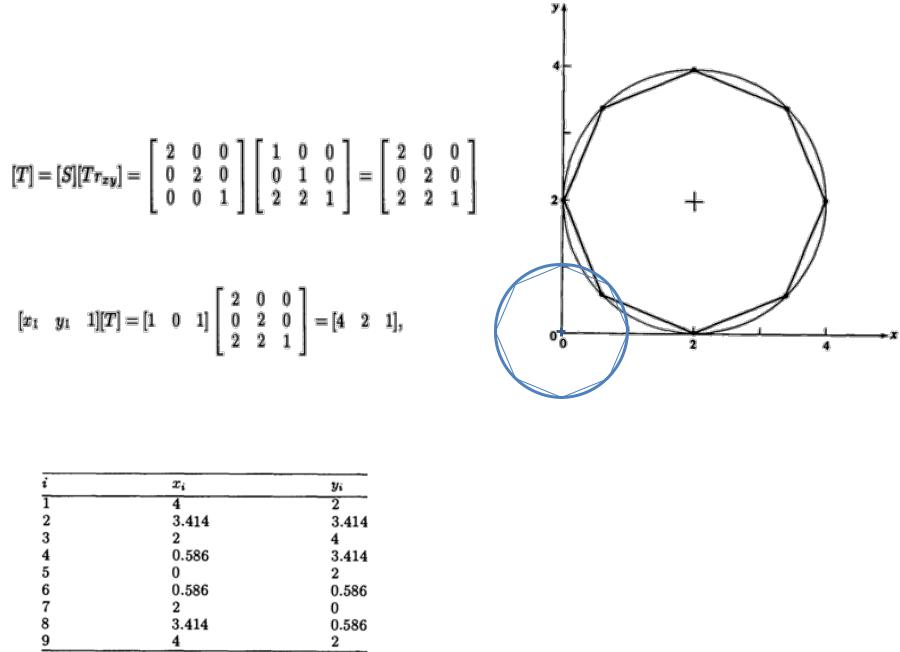
•Рассмотрим 3x3 преобразование, которое масштабирует полученные результаты с коэффициентом 2 и переносит центр окружности в точку (2,2):

•Применяя это преобразование к точке (х,у), получаем.

•Полный результат приведен в таблице 2 и на рис. 5.

•Таблица 2 Результаты для окружности радиуса 2 с центром в (2,2)

•Рис. 5 Единичная параметрическая окружность с n = 8.

Напоминаем -параметр θ — геометрический угол, отмеряемый против часовой стрелки от положительной полуоси х.

ПАРАМЕТРИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ ЭЛЛИПСА

1.Для окружности достаточно хорошее представление получается при соединении отрезками равномерно распределенные точки. Однако, для эллипса изображение будет неверным, как показано штриховой линией на рис. 6. Особенно на концах, кривизна слишком велика и требуется большее количество точек.

2.Другой метод построения основан на равных приращениях по периметру и дает хороший результат для достаточно большого количества точек. Недостатки - указывается слишком много точек на сторонах с малой кривизной, и вычисление равных частей периметра требует сложного расчета эллиптического интеграла.

3.Компромисс – неравномерное распределение: малые приращения параметра у концов, где кривизна велика, и большие приращения параметра вдоль сторон. Такое распределение точек получается из параметрического представления эллипса с центром в начале координат, большой полуосью а и малой полуосью b:

•х = acosθ,

• у = bsinθ,

()

Рис. 6 Равноугольное представление сильно вытянутого эллипса.

•где θ — параметр. Диапазон от 0 до 2 задает полный эллипс. Требуемое распределение точек порождается равномерными приращениями параметра θ.