2468

6.8.z = xe y / x ;

6.9.z = sin(x + ay);

6.10.z = cos y + (y − x)sin y ;

6.11. u = 1 e− x2 / 4ta2 ;

t

6.12. z = exy ;

6.13. z = ln( x + y );

6.14. z = x sin( y / x) ;

6.15. z = ex / y ln y ;

6.16. u = arctg(2x − t);

6.17. z = ex / y ;

6.18. u = (x − y)( y − z)(z − x) ;

6.19. z = ln(x2 + xy + y2 ) ;

6.20. z = cos( y / x) ;

6.21.	u = 1/ x2 + y2 + z2 ;
6.22.	z = cos(x2 + y2 ) ;

6.23. z = ex2 + y2 ;

6.24. u = ex (x cos y − y sin y) ;

6.25. u = cos(x − at)+ sin(x + at) ; 6.26. u = x cos(x − y)+ y sin(x + y) ;

6.27. u = xey + yex ;

6.28. z = y ln(x2 − y2 );

	6.29.	z =	x2	+	x	+	1	−	1	;
			2 y		2		x		y
	6.30. z = yex2 − y2					;

x2 z′′	+ 2xyz′′	+ y2 z′′
xx	xy	yy

z′′

− a2 z

′′

= 0 .

yy

xx

(x − y)z′′

= z′ .

xy

y

u′

− a2u′′

= 0 .

t

xx

x2 z′′

− 2xyz′′

+ y2 z′′

xx

xy

yy

xz

′

+ yz

′

= 0,5 .

x

y

xz

′

+ yz

′

= z / 2 .

x

y

xz

′

+ yz

′

= z / ln y .

x

y

u′′

+ 2u′′

= 0 .

xx

xt

yz

′′

− z′

+ z

′

= 0 .

xy

y

x

u′

+ u′

+ u

′

= 0 .

x

y

z

xz

′

+ yz′

= 2 .

x

y

xz

′

+ yz′

= 0 .

x

y

u′′

+ u

′′

+ u′′

= 0 .

xx

yy

zz

yz

′

− xz′

= 0 .

x

y

yz

′

− xz′

= 0 .

x

y

u′′

+ u

′′

= 0 .

xx

yy

a2u′′

− u

′′

= 0 .

xx

tt

u′′

− 2u′′

+ u′′

= 0 .

xx

xy

yy

u′′

+ u

′′

= xu .

xx

yy

1

z

′

+

1

z

′

=

z

.

y

x

x

y

y2

x2 z′

+ y2 z

′

=

x3

.

x

y

y

1

z

′

+

1

z

′

=

z

.

y

x

x

y

y2

=0 .

+2xyz = 0 .

21

З А Д А Н И Е № 7

Даны функция z = f (x, y) и точка М(х, у). С помощью полного дифференциала вычислить приближенное значение функции z = f (x, y) в данной точке. Вычислить точное значение функции в точке М0(х0, у0) и оценить относительную погрешность вычислений.

7.1.	z = 2x2 − 3y2 + 2x −1 ;	М(1,02; 0,95);	М0(1; 1).
7.2.	z = 4x2 − 3y2 + 7xy − 2 ;	М(0,09; 0,99);	М0(0; 1).
7.3.	z = 3x2 + y2 − 4x ;	М(1,02; 0,95);	М0(1; 1).
7.4.	z = 5x2 − y2 + 2 y − 2 ;	М(1,02; 4,05);	М0(1; 4).
7.5.	z = 3x2 + 2 y2 − 5x + 6 ;	М(3,01; 2,03);	М0(3; 2).
7.6.	z = x2 − y2 + 3xy −1 ;	М(2,01; 2,95);	М0(2; 3).
7.7.	z = x2 + xy + y2 ;	М(1,02; 1,96);	М0(1; 2).
7.8.	z = 3x2 − xy + x + y ;	М(1,06; 2,92);	М0(1; 3).
7.9.	z = x2 + 3xy − 6 y ;	М(3,96; 1,03);	М0(4; 1).
7.10.	z = x2 − y2 + 6x + 3y ;	М(2,02; 2,97);	М0(2; 3).
7.11.	z = x2 + 2xy + 3y2 ;	М(1,96; 1,04);	М0(2; 1).
7.12.	z = x2 + y2 + 2x + y −1 ;	М(1,98; 3,91);	М0(2; 4).
7.13.	z = 3x2 + 2 y2 − xy ;	М(–0,98; 2,97);	М0(–1;3).
7.14.	z = x2 − y2 + 5x + 4 y ;	М(3,02; 2,98);	М0(3; 3).
7.15.	z = 2xy + 3y2 − 5x ;	М(3,04; 3,95);	М0(3; 4).
7.16.	z = xy + 2 y2 − 2x ;	М(0,97; 2,05);	М0(1; 2).
7.17.	z = x2 − 3xy − 4 y ;	М(3,01; 3,98);	М0(3; 4).
7.18.	z = 5x2 − 3y2 + 2 ;	М(0,85; 3,98);	М0(1; 4).
7.19.	z = 2x2 − y2 − 6x ;	М(2,01; 0,97);	М0(2; 1).
7.20.	z = y2 − 4x2 + 2 ;	М(1,98; 3,03);	М0(2; 3).
7.21.	z = 5y2 + 3x2 −1;	М(1,03; 0,98);	М0(1; 1).
7.22.	z = x2 + y2 − 2x + 2 y ;	М(1,08; 1,94);	М0(1; 2).
7.23.	z = x2 + y2 − 4x + 2 y ;	М(2,98; 2,05);	М0(3; 2).
7.24.	z = 2 y2 + 9x + y ;	М(1,96; 1,04);	М0(2; 1).
7.25.	z = 2x2 + 3xy + y2 ;	М(0,96; 1,95);	М0(1; 2).
		22

7.26.	z = x2 + y2 + 3x + 2 y − 1;		М(2,98; 3,91);	М0(3; 4).
7.27.	z = x2	+ 2xy − 3y2 ;	М(2,97; 0,99);	М0(3; 1).
7.28.	z = x2	+ 2xy − 5y ;	М(4,98; –2,01);	М0(5; –2).
7.29.	z = x2	− y2 + 6x + 3y ;	М(1,97; 2,98);	М0(2; 3).
7.30.	z = 3x2 + 2 y2 − x ;		М(–1,02; 3,03);	М0(–1; 3).

З А Д А Н И Е № 8

Дана функция z = f (x, y), точка А(х0; у0) и вектор а . Найти а) grad z в точке А и его численное значение; б) производную функции в точке А по направлению

вектора а .
8.1.	z = 2x2 + xy ;	А(–1; 1);	а = 3i + 4 j .
8.2.	z = 5x2 y + 3xy2 ;	А(1; –1);	а = 6i − 8 j .
8.3.	z = 3x2 y − xy3 ;	А(–1; 1);	а = i − j .
8.4.	z = 5x2 y − 4xy ;	А(3; 4);	а = 3i − 5 j .
8.5.	z = 6xy2 − 7x + 2 ;	А(2; 3);	а = 4i − 3 j .
8.6.	z = 4x2 y − 3x + 2 y ;	А(2; 2);	а = 2i − 3 j .
8.7.	z = x3 y + xy2 ;	А(1; 3);	а = −5i + 12 j .
8.8.	z = 5x2 − 2xy + y2 ;	А(1; 1);	а = 2i − j .
8.9.	z = 6x3 y − 5y + 7x2 ;	А(1; 2);	а = 3i − 4 j .
8.10.	z = 6x2 − 3xy + y3 ;	А(1; –2);	а = i + 2 j .
8.11.	z = x3 + 2xy + y2 ;	А(–1; 2);	а = 3i − 4 j .
8.12.	z = x2 + xy + y2 ;	А(1; 1);	а = 2i − j .
8.13.	z = 2x2 + 3xy + y2 ;	А(2; 1);	а = 3i − 4 j .
8.14.	z = 3x2 − 5y2 + x ;	А(–1; 1);	а = 3i + 2 j .
8.15.	z = 3x2 − 6x2 y ;	А(1; 1);	а = 2i − 4 j .
8.16.	z = 5x2 + 4xy ;	А(2; 1);	а = i + 2 j .
8.17.	z = x2 + y2 − 7 y ;	А(2; 3);	а = 4i − 3 j .
8.18.	z = 3x2 − 2xy ;	А(1; 2);	а = −5i + 2 j .
8.19.	z = 5y2 + 4x − 2 y ;	А(1; 3);	а = 2i − j .
8.20.	z = 3x4 + 2x2 y2 ;	А(–1; 2);	а = 4i − 3 j .
		23

8.21.	z = 3x2 y3 + 5xy2 ;			А(1; 1);					а = 2i + j .
8.22.	z = x2 + xy + y2 + 2x + 2 y ;			А(1; 1);					а = 3i + 4 j .
8.23.	z = x3 y − 5xy2 + 8 ;			А(1; –1);					а = i + j .
8.24.	z = 6x2 − 3xy + 4 y ;			А(1; 2);					а = 6i + 8 j .
8.25.	z = 2x2 + 2x − y ;			А(0; 3);					а = i − j .
8.26.	z = x2		− xy + y2 ;	А(1; –1);					а = −6i + 8 j .
8.27.	z = 3x2 − 2x + y ;			А(1; 1);					а = −3i + 4 j .
8.28.	z = x + 4 y2 − 2xy ;			А(3; 4);					а = i − j .
		2			1		3
8.29.	z = x		− xy + 3y ;	A −		;		;	а = 6i + 8 j .
					3		4
8.30.	z = x2		− 2xy + 3y − 1;	А(1; 2);					а = 3i − 4 j .

З А Д А Н И Е № 9

Найти наибольшее и наименьшее значения функции z = f (x, y) в ограниченной замкнутой области D. Область D изобразить на чертеже.

10.1.z = x3 + y3 – 3xy;

10.2.z = x2 – y2;

10.3.z = x2 – xy + y2 – 4x;

10.4.z = x2 + 3y2 + x – y;

10.5.z = 0,5x2 – xy;

10.6.z = x2 – xy + y2 + x + y;

10.7.z = 2x2 – 6xy + 3y2 – y;

10.8.z = x2 – xy – 2;

10.9.z = 10 – x2 + 2xy;

10.10.z = x2 + 2xy – y2 + 4x;

10.11.z = x2 – y2 + 3xy + 7;

10.12.z = x2 + 2y2 – 1;

10.13.z = 3 – x2 – xy – y2;

10.14.z = x2 + y2 + x – y;

10.15.z = x2 +2xy + 2y2;

10.16.z = 3x2 – 3xy +y2 + 1;

10.17.z = 5 + 2xy – x2;

10.18.z = x2 – 2xy – y2 + x;

10.19.z = x2 – xy – 2;

10.20.z = x2 + xy + 3y2;

10.21.z = xy (1 – x – у);

D: 0 ≤ x ≤ 2, –1 ≤ y ≤ 2.

D: x2 + y2 ≤ 1.
D: x ≥ 0,	y ≥ 0; 2x + 3y – 12 ≤ 0.
D: x ≤ 1,	y ≤ 1, x + y ≤ 1.

D: y ≥ x2 / 3;		y ≤ 3.
D: x ≤ 0,	y ≤ 0;	x + y ≥ –3.
D: x ≥ 0,	y ≤ 2; y ≥ x2 / 2.

D: 4x2 – 4 ≤ y ≤ 0; –1≤ y ≤ 2. D: 0 ≤ y ≤ 4 – x2; –1≤ y ≤ 2.

D: x ≤ 0, y ≤ 0; x + y ≥ –3. D: –2 ≤ x ≤ 2, –2 ≤ y ≤ 2. D: x ≥ –2, y ≥ –2, x + y ≤ 4. D: x ≤ 1, y ≥ –1, x +1 ≥ y. D: x ≥ 1, y ≥ –1, x + y ≤ 2. D: –1 ≤ x ≤ 1, –1 ≤ y ≤ 3.

D: x ≥ –1, y ≥ –1, x + y ≤ 1. D: –1 ≤ y ≤ 4 – x2.

D: x ≤ 0, y ≤ 1, x + y + 2 ≥ 0. D: 4x2 – 4 ≤ y ≤ 1.

D: –1 ≤ x ≤ 1, –1 ≤ y ≤ 1. D: х ≥ 0, у ≥ 0, х + у ≤ 2.

24

10.22. z = 3х2 + 3у2 – 2х – 2у + 2;			D: х ≥ 0,	у ≥ 0,	х + у ≤ 1.
10.23. z = х3	+ у3 – 3ху;		D: х ≥ 0,	у ≥ 0,	х + у ≤ 3.
10.24. z = х2у (2 – х – у);			D: х ≥ 0,	у ≥ 0,	х + у ≤ 6.
10.25. z = z = х2у;			D: х2 + у2 ≤ 1.
10.26. z = х2	+ 2ху – у2	– 4х;	D: х ≤ 3,	у ≥ 0,	у ≤ 2х.
10.27. z = х2	+ 2ху – у2	– 2х + 2у;	D: 0 ≤ х ≤ 2, у ≥ 0, у – х ≤ 2.
10.28. z = х2у (4 – х – у);			D: х ≥ 0, у ≥ 0,		х + у ≤ 6.
10.29. z = 2х3 + 4х2 + у2 – 2ху;			D: у ≥ х2,	у ≤ 4.
10.30. z = 3ху;			D: х2 + у2 ≤ 2.

З А Д А Н И Е № 1 0

Экспериментально получены пять значений искомой функции y = f (x) при пяти значениях аргумента, которые записаны в таблице. Методом наименьших квадратов найти функцию y = f (x) вида y = ax + b.

10.1.	хi	1	2	3	4	5	10.2.	хi	1	2	3	4	5
	yi	3,2	4,2	2,7	0,7	1,2		yi	3,4	4,4	2,9	0,9	1,4
10.3.							10.4.
	хi	1	2	3	4	5		хi	1	2	3	4	5
	yi	3,6	4,6	3,1	1,1	1,6		yi	3,8	4,8	3,3	1,3	1,8
10.5.							10.6.
	хi	1	2	3	4	5		хi	1	2	3	4	5
	yi	4	5	3,5	1,5	2		yi	2,8	3,8	2,3	0,3	0,8
10.7.							10.8.
	хi	1	2	3	4	5		хi	1	2	3	4	5
	yi	4,1	5,1	3,6	1,6	2,1		yi	4,4	5,4	3,9	1,9	2,4
10.9.							10.10.
	хi	1	2	3	4	5		хi	1	2	3	4	5
	yi	4,6	5,6	4,1	2,1	2,6		yi	4,8	5,8	4,3	2,3	2,8
10.11.							10.12.
	хi	1	2	3	4	5		хi	1	2	3	4	5
	yi	4,3	5,3	3,8	1,8	2,3		yi	4,5	5,5	4,0	2,3	2,5
10.13.							10.14.
	хi	1	2	3	4	5		хi	1	2	3	4	5
10.15.	yi	4,7	5,7	4,2	2,2	2,0	10.16.	yi	4,9	5,9	4,4	2,4	2,9
	хi	1	2	3	4	5		хi	1	2	3	4	5
	yi	5,0	6,1	4,6	2,6	3,1		yi	3,9	4,9	3,4	1,4	1,9
10.17.							10.18.
	хi	1	2	3	4	5		хi	1	2	3	4	5
	yi	5,2	6,2	4,7	2,7	3,2		yi	5,5	6,5	5,0	3,0	3,5
10.19.							10.20.
	хi	1	2	3	4	5		хi	1	2	3	4	5
	yi	5,7	6,7	5,2	3,2	3,7		yi	5,9	6,9	5,4	3,4	3,8
							25

10.21.	хi	1	2	3	4	5	10.22.	хi	1	2	3	4	5
	yi	4,3	5,3	3,8	1,8	2,8		yi	4,5	5,5	4,0	2,3	2,7
10.23.							10.24.
	хi	1	2	3	4	5		хi	1	2	3	4	5
	yi	4,7	5,7	4,2	2,2	2,7		yi	4,9	5,9	4,4	2,5	2,3
10.25.							10.26.
	хi	1	2	3	4	5		хi	1	2	3	4	5
	yi	5,1	6,1	4,6	2,6	3,1		yi	3,9	4,9	3,4	1,6	1,2
10.27.							10.28.
	хi	1	2	3	4	5		хi	1	2	3	4	5
	yi	5,2	6,2	4,7	2,8	3,1		yi	5,5	6,5	5,4	3,1	3,5
10.29.							10.30.
	хi	1	2	3	4	5		хi	1	2	3	4	5
	yi	5,7	6,7	5,2	3,4	3,0		yi	5,9	6,9	5,4	3,4	3,9

З А Д А Н И Е № 1 1

Составить уравнения касательной плоскости и нормали к поверхности S в точке М0(х0, у0, z0). Записать нормальный вектор к поверхности S в точке

М0(х0, у0, z0).

11.1.	S: x2 + y2 + z2 + 6z – 4x + 8 = 0,	M0(2, 1, –1).
11.2.	S: x2 + z2 – 4y2 = –2xy,	M0(–2, 1, 2).
11.3.	S: x2 + y2 + z2 + 3z – xy = 7,	M0(1, 2, 1).
11.4.	S: x2 + y2 + z2 + 6y + 4x = 8,	M0(–1, 1, 2).
11.5.	S: 2x2 – y2 + z2 – 4z + y = 13,	M0(2, 1, –1).
11.6.	S: x2 + y2 + z2 – 6y + 4z + 4 = 0,	M0(2, 1, –1).
11.7.	S: x2 + z2 – 5yz + 3y = 46,	M0(1, 2, –3).
11.8.	S: x2 + y2 – xz – yz = 0,	M0(0, 2, 2).
11.9.	S: x2 + y2 + 2yz – z2 – y – 2z = 2,	M0(1, 1, 1).
11.10.	S: x2 + y2 – z2 – 2xz + 2x – z = 0,	M0(1, 1, 1).
11.11.	S: z = x2 + y2 – 2xy + 2x – y,	M0(–1, –1, –1).
11.12.	S: z = –x2 + y2 + 2xy – 3y,	M0(1, –1, 1).
11.13.	S: z = x2 – y2 – 2xy – x – 2y,	M0(–1, 1, 1).
11.14.	S: x2 – 2y2 + z2 + xz – 4y – 13 = 0,	M0(3, 1, 2).
11.15.	S: 4y2 – z2 + 4xy – xz + 3z = 9,	M0(1, –2, 1).
11.16.	S: z = x2 + y2 – 3xy – x + y + 2,	M0(2, 1, 0).
11.17.	S: 2x2 – y2 + 2z2 + xy + xz = 3,	M0(1, 2, 1).
11.18.	S: x2 – y2 + z2 – 4х + 2y = 14,	M0(3, 1, 4).
11.19.	S: x2 + y2 – z2 + xz + 4у = 4,	M0(1, 1, 2).
11.20.	S: x2 – y2 – z2 + xz + 4x = –5,	M0(–2, 1, 0).
11.21.	S: x2 + y2 – xz + yz – 3x = 11,	M0(1, 4, –1).
11.22.	S: x2 + 2y2 + z2 – 4xz = 8,	M0(0, 2, 0).
11.23.	S: x2 – y2 – 2z2 – 2y = 0,	M0(–1, –1, 1).
11.24.	S: x2 + y2 – 3z2 + xy = –2z,	M0(1, 0, 1).
	26

11.25.	S: 2x2 – y2 + z2 – 6x + 2y = –6,			M0(1, –1, 1).
11.26.	S: x2 + y2 – z2 + 6xy – z = 8,			M0(1, 1, 0).
11.27.	S: z = 2x2 – 3y2 + 4x – 2y + 10,			M0(–1, 1, 3).
11.28.	S: z = x2	+ y2 – 4xy + 3x – 15,		M0(–1, 3, 4).
11.29.	S: z = x2	+ 2y2 + 4xy –	5y – 10,	M0(–7, 1, 8).
11.30.	S: z = 2x2 – 3y2 + xy +		3x + 1,	M0(1, –2, 2).

Р Е Ш Е Н И Е З А Д А Ч Т И П О В О Г О В А Р И А Н Т А К О Н Т Р О Л Ь Н О Й Р А Б О Т Ы № 4

2 З а д а н и е

№

6 .

Дана функция z = e− cos(x + 3y) . Показать, что F=0,

где F = 9

∂ 2 z

−

∂ 2 z

.

∂x2

∂y2

Р е ш е н и е .

Вычислим

∂z

;

∂z

;

∂ 2 z

;

∂ 2 z

:

∂x

∂y

∂x2

∂y

2

∂z

= e−cos(x+3 y) sin(x +

3y);

∂z

= e−cos(x+3 y) sin(x + 3y) 3 ;

∂x

∂y

∂ 2 z = (e−cos( x+3 y) sin(x + 3y))′ = e−cos( x+3 y)

sin 2 (x + 3y) + e− cos( x+3 y) cos(x + 3y) ;

∂x2

x

∂ 2 z

= (3e−cos(x+3 y) sin(x + 3y))′

= 9e−cos( x+3 y)

sin 2 (x + 3y) + 9e− cos( x+3 y) cos( x + 3y) .

∂y2

y

Тогда

F

= 9

∂ 2 z −

∂ 2 z

= 9(e−cos( x+3 y) sin 2 (x + 3y) + e−cos( x+3 y) cos(x + 3y)) −

∂x2

∂y2

− 9e− cos(x+3 y) sin 2 (x + 3y) − 9e− cos(x+3 y) cos(x + 3y) = 0 .

Ответ:

F ≡ 0 , что и требовалось доказать. v

2 З а д а н и е

№

7 .

Даны функция

z = x2 + 2xy − 3y2 и точка M(1,97;

0,99). С помощью полного дифференциала вычислить приближенное значение функции z = f (x, y) в данной точке. Вычислить точное значение функции в точке M0(2; 1) и оценить относительную погрешность вычислений.

Р е ш е н и е . Найдем частные производные и полный дифференциал данной функции в любой точке (х, у)

	∂z	= 2x + 2 y ,		∂z	= 2x − 6 y .
	∂x			∂y
Тогда полный дифференциал dz = (2x + 2 y)dx + (2x − 6 y)dy .
Вычислим dz в точке М0(2, 1) при приращениях
dx = x = х – х0 = 1,97 − 2 = −0,03,			dy ≈ y = у – у0 = 0,99 − 1 = −0,01,
			27

dz = (2 2 + 2 1)(−0,03) + (2 2 − 6 1)(0,01) = −0,18 + 0,02 = −0,16. Найдем z(M0) = 22 + 2 2 1 − 3 12 = 5.

Тогда z = z(M ) ≈ z(M 0 ) + dz = 5 − 0,16 = 4,84 – приближенное значение функ-

ции в точке М.

Вычислим точное значение функции z в точке М

z = 1,972 + 2 1,97 0,99 − 3 0,992 = 3,8809 + 3,9006 − 2,9403 = 4,8412.

Найдем относительную погрешность

	δ =		z − z		100 % =	4,8412 − 4,84	100 % ≈ 0,025 %
			z			4,84

Ответ: Приближенное значение z = 4,84 , относительная погрешность δ ≈ 0,025 % . v

2З а д а н и е 8 . Дана функция z = 3x2 − 5xy + 7y; точка А(2, 1) и вектор

а= (4, 3) . Найти а) grad z в точке А и его численное значение; б) производную

вточке А по направлению вектора а .

Р е ш е н и е . а) По определению градиента grad z =

∂z

i

+

∂z

j .

∂x

∂y

Значение градиента в точке А определяется по формуле

grad z

A

=

∂z

i

+

∂z

j .

∂x

∂y

A

A

Найдем частные производные в точке А

∂z

= 6 2 − 5 1 = 7 ;

∂z

= −5 2 − 7 = −3 .

= 6x − 5y

= −5x − 7

∂x

A

A

∂y

A

A

Следовательно, grad z

A

= 7i − 3 j ,

grad z

A

=

72 + (−3)2 =

58 – численное

значение grad z( А) .

б) Производную от функции z по направлению вектора a

в точке А опреде-

лим из соотношения

∂z

∂z

cos α +

∂z

cosβ ,

=

∂а

∂x

∂y

A

A

A

где cos α и cos β – направляющие косинусы данного вектора a = (аx , ay ) , кото-

рые вычисляются по формулам

cos α =

a

x

; cosβ =

ay

; a

= ax2 + a2y . Тогда

a

a

a = 42 + 32 = 25 = 5 , cos α =

4

; cosβ =

3

,

5

5

28

∂z

= 7

4

− 3

3

=

28

−

9

= 3

4

.

∂a

A

5

5

5

5

5

∂z

Ответ: grad z

A

= 7i − 3 j ;

grad z

=

58 ;

= 3,8 . v

A

∂a

A

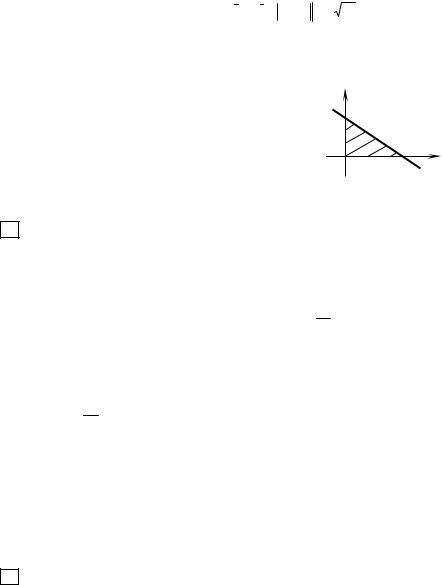
2 З а д а н и е 9 . Найти наибольшее и наименьшее значения функции

z= х2 + 4ху – у2 – 6х – 2у

вобласти D: x ≥ 0, y ≥ 0; 2x + 3y – 6 ≤ 0. Выполнить чертеж области D.

Р е ш е н и е .	1.	Найдем критические точки функ-
ции z = х2 + 4ху – у2 – 6х – 2у:
z′ = 2х + 4у – 6;			z′	= 4х – 2у – 2.
x			y
Решим систему уравнений
2x + 4 y − 6 = 0,			x = 3 − 2 y,			x = 1,
				2 y = 2
4x − 2 y − 2 = 0			4(3 − 2 y) −			у = 1,

y

B

2

D A

0	3	x
	Р и с. 6

и получим одну стационарную точку (1; 1), которая лежит внутри заданной области (рис. 6).

2. Найдем наибольшее и наименьшее значения z = f (x, у) на границе области, которую составляют отрезок ОА оси Ох; отрезок OВ оси Оу; отрезок AB прямой.

На отрезке ОА: у = 0; 0 ≤ х ≤ 3

z = f (x, 0) = х2 – 6х

(непрерывная функция одной переменной). Из уравнения dxdz = 0, т. е.

2х – 6 = 0,

имеем х = 3 (критическая точка, не являющаяся внутренней).

На отрезке OB: х = 0, 0 ≤ y ≤ 2

z = f (0, у) = –у2 –2 у.

Из уравнения ddzу = 0, т. е.

–2у – 2 = 0,

имеем у = –1; эта точка лежит вне отрезка [0, 2] и поэтому нас не интересует.

На отрезке АВ имеем
	х = 3 – 1,5у;		0 ≤ у ≤ 2,
	z = –9 + 10y – 19у2 /4,		0 ≤ у ≤ 2.
Из уравнения	dz	= 0, т. е. 10 – 19y / 2 = 0, найдем у = 20		/ 19, что дает z(20 /
	dy

19)= –71 / 19.

3.В точках стыка участков граница имеем следующие значения f (x, у):

f (О) = f (0, 0) = 0;	f (В) = f (0, 2) = –8;	f (А) = f (3, 0) = –9.
	29

4. Сравнивая между собой вычисленные значения f (x, у), т. е. числа –4, –71 / 19, 0, –8, –9, приходим к заключению, что свое набольшее значение в данном замкнутом треугольнике функция принимает в точке О(0; 0), наименьшее –

в точке А(3, 0), при этом z наиб = z(0; 0) = 0; z наим = z(3; 0) = –9.

Ответ: z наиб = z(0; 0) = 0; z наим = z(3; 0) = –9. v

2 З а д а н и е 1 0 . Экспериментально получены пять значений искомой функции y = f (x) при пяти значениях аргумента, которые записаны в таблице. Методом наименьших квадратов найти функцию y = f (x) в виде y = ax + b.

xi

1

2

3

4

5

yi

0,5

1

1,5

2

3

Р е ш е н и е .

Составим систему

n

n

n

∑ yi xi − a∑xi2 − b∑xi = 0,

i=1

i=1

i=1

(1)

n

n

∑ yi − a∑xi − bn = 0.

i=1

i=1

Для этого предварительно вычислим суммы

5

5

∑xi

= 1+ 2 + 3 + 4 + 5 = 15 ;

∑ yi = 0,5 + 1+ 1,5 + 2 + 3 = 8 ;

i=1

i=1

5

5

∑xi2 = 12 + 22 + 32 + 42 + 52 = 55 ;

∑xi yi = 1 0,5 + 2 1+ 3 1,5 + 4 2 + 5 3 = 30 .

i=1

i=1

Подставим полученные значения в систему (1)

15b + 55a = 30,

у

3,0

= 8.

у = 0,6x − 0,2

5b + 15a

2,5

Умножим второе уравнение на (−3)

2,0

и сложим с первым, тогда

1,5

10а = 6

а = 0,6.

1,0

Подставим значение а = 0,6 во

0,5

второе уравнение и получим

0

1

2

3

4

5 х

5b + 9 = 8;

b = −0,2.

Следовательно, наилучшее при-

Р и с. 7

ближение представляется формулой

y = ax + b = 0,6x − 0,2.

Построим график этой зависимости и нанесем на него экспериментальные точки (рис. 7).

Ответ: y = 0,6x − 0,2. v

30