Основы Теории погрешностей

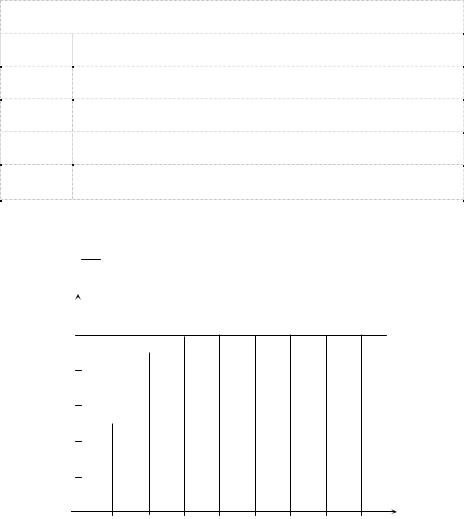
Gorozhankin Alexey Anatolievich (alias − Galan) Russia Samara 2004

ить результирующий график путем перемножения графиков, представленных на рис. 1 и рис. 2. Для простоты расчетов и более адекватного понимания всей сути процессов, происходящих при сложении, график на рис. 2 немного упростим, приняв n = 8, тем самым, представив оба графика к одной координатной сетке. Результирующий график также будет иметь некоторые прямые для каждого числового интервала, которые изменяются от 0

до какого-то максимального значения, вычисленного в примере 9 (рис. 3).

	Пример 9
n = 1	50 % · 0.0000001 = 0.5 . 10–5
n = 2	9.0909.. % · 0.000001 = 0.90909.. · 10–5
n = 3	0.990099.. % · 0.00001 = 0.990099.. · 10–5
n = 4	0.09990009.. % · 0.0001 = 0.9990009.. · 10–5
n = ∞	1 · 103–n

δx1 X1 10− 5 , %

Z

1

0.8

0.6

0.4

0.2

Nчи

0

1

2

3

4

5

6

7

8

Рис. 3. Условный график изменения погрешностей

с тильдой при L-округлении

31

Gorozhankin Alexey Anatolievich (alias − Galan) Russia Samara 2004

Таким образом, получен условный график изменения погрешностей с тильдой при L-округлении. Анализируя данный график, можно сделать вывод, что при увеличении номера числового интервала уровни изменения погрешности с тильдой принимают одинаковый вид. Это означает, что при использовании у слагаемых чисел одинакового количества знаков после знака дробности каждый числовой интервал в плане изменения погрешности с тильдой, как впрочем, и точности с тильдой равноценен. Все довольно просто: слагаемые числа меньших числовых интервалов обладают малой величиной, но бóльшими значениями погрешностей, и наоборот, слагаемые числа бóльших числовых интервалов обладают большой величиной, но малыми значениями погрешностей. При использовании же у слагаемых чисел одинакового количества знаков от начала числа, как при умножении и делении, такой четкой картины не наблюдается, т.к. в этом случае слагаемые числа каждого числового интервала могут обладать любыми погрешностями при неизменном втором факторе, что естественно, не может привести к равновесию погрешностей и точностей с тильдой. Примерно похожая картина наблюдается и при использовании других методов округления, а также при сложении отрицательных чисел, поэтому можно сделать вывод, что:

При сложении n чисел следует оставлять k точных знаков после

знака дробности.

32

Gorozhankin Alexey Anatolievich (alias − Galan) Russia Samara 2004

Приведенное доказательство, конечно же, является довольно условным, но тем не менее основные принципы, заложенные в нем, присутствуют как при сложении двух чисел, так и при сложении большего количества чисел. Для полноты картины необходимо привести пример вычисления чисел, показывающий стремление к равновесию погрешностей с тильдой при использовании k знаков после знака дробности, применив округление чисел по погрешности (пример 10). Для этой цели использовались числа разного порядка, у которых погрешности имеют круглые значения (10 %,

1 %, 0.1 % и т.п.), причем при одинаковом количестве точных знаков погрешности чисел равны. Такие числа состоят из знаков одинаковой величины.

Пример 10

3

Z

∑ Xi

0.111... + 44.44... + 9999.99...

10044.555...

i = 1

3

Zпр

∑ Xпрi

0.11 + 44.44 + 9999.99

10044.54

i = 1

δ

Z− Zпр

100%

10044.55...− 10044.54

100%

1.548.. 10−4%

z

Z

10044.55...

δx1 = 1 %

δx2 = 0.01 %

δx3 = 0.0001 %

~

~

~

0.9955.. 10− 4%

δx1

0.1106.. 10− 4% δx2

0.4424.. 10−4% δx3

δzф = (0.1106.. + 0.4424.. + 0.9955..) · 10–4 = 1.548.. · 10–4 %

33

Gorozhankin Alexey Anatolievich (alias − Galan) Russia Samara 2004

Из приведенного примера видно, что погрешности с тильдой слагаемых чисел отличаются друг от друга не более чем на один порядок, хотя третье число больше первого на четыре порядка. Это доказывает правильность использования при сложении k знаков после знака дробности. При использовании в этом примере k знаков от начала числа приводит к большему отличию погрешностей с тильдой (пример 11).

Пример 11

3

Zпр ∑ Xпрi 0.1111 + 44.44 + 9999 10043.5511

i = 1

δ

Z− Zпр

100%

10044.55...− 10043.5511

100%

100 10−4%

z

Z

10044.55...

~

0.001106.. 10−4%

~

0.4424.. 10−4%

~

99.55.. 10−4%

δ

δ

δ

x1

x2

x3

δzф = (0.001106.. + 0.4424.. + 99.556..) · 10–4 = 100 · 10–4 %

Примечание: за основу взяты данные, представленные в примере 10.

Использование k знаков от начала числа, как при умножении и делении, привело к очень большому разбросу между величинами погрешностей с тильдой, поэтому ни о каком их стремлении к равновесию и речи быть не может, например, погрешность с тильдой третьего числа больше аналогичного показателя первого числа более чем в 90000 раз. К тому же следует учитывать тот факт, что погрешность окончательного результата в этом

34

Gorozhankin Alexey Anatolievich (alias − Galan) Russia Samara 2004

случае в несколько десятков раз превышает погрешность при использовании k знаков после знака дробности, полученную в примере 10, что в ка- кой-то мере доказывает менее продуктивное использование у чисел k знаков от начала числа при сложении. Иначе и быть не может, ведь ясно и без доказательств, что неправильно использовать неодинаковое количество знаков после знака дробности у слагаемых чисел, т.к. это приводит к нерациональному накоплению (читай: сложению) знаков, например, одно число округлено до десятков, второе – до единиц, третье – до тысячных долей единицы, т.е. третье число вносит в копилку величины окончательного результата даже тысячные доли единицы, а первое и второе числа вносят соответственно только десятки и единицы – это коренным образом неверно.

Что же касается вычитания, то для него также можно привести доказательство использования в расчетах k знаков после знака дробности, но в этом нет особого смысла, т.к. оно будет построено на тех же самых принципах, что и для сложения, лишь с незначительными изменениями. Поэтому при вычитании чисел нужно руководствоваться следующим условием:

При вычитании n чисел следует оставлять k точных знаков после

знака дробности.

35

Gorozhankin Alexey Anatolievich (alias − Galan) Russia Samara 2004

Исследования показывают, что при сложении и вычитании при использовании у чисел k знаков после знака дробности приводит к более равномерному распределению погрешностей и точностей с тильдой, чем при использовании других способов округления чисел.

Основными видами вычислений чисел, как известно, являются умножение, деление, сложение и вычитание, которые подробно были рассмотрены в данной статье. Но, тем не менее, существует множество других, менее распространенных видов вычислений, таких как степенная функция, логарифмическая функция, различные тригонометрические функции, интеграл, производная и другие, которые подробно рассмотрены в (1).

На практике же в большинстве случаев существуют различные сочетания этих простейших вычислений, и лишь в редких случаях встречаются расчеты только с каким-нибудь одним видом, например, умножение нескольких чисел. Поэтому необходимо изучить поведение чисел и их числовых характеристик в различных расчетах, ведь для каждого вида простейших вычислений существуют свои формулы и свои способы образования приближенных чисел, использование которых приводит к некоторой несовместимости между простейшими вычислениями. Для преодоления всех шероховатостей нужно разработать правила вычисления чисел в сложных расчетах или, иными словами, попытаться все виды вычислений объединить в одно целое.

36

Gorozhankin Alexey Anatolievich (alias − Galan) Russia Samara 2004

К любому расчету можно подойти разными путями. Например, используя принцип от простого к сложному, можно разделить любой пример на несколько простейших вычислений и сгруппировать их по степени значимости, как это обычно делается в элементарной математике, а затем последовательно определять числовые характеристики (Блочный принцип). Можно рассматривать примеры и в обратном направлении, только в этом случае придется все формулы определения числовых характеристик простейших вычислений объединить в одну общую формулу, по которой и будут найдены числовые характеристики окончательного результата (Формульный принцип). Ну и, конечно же, можно использовать комбинацию этих вариантов (Блочно-формульный принцип).

В различных видах простейших вычислений используются два способа оставления знаков у чисел, иначе говоря, сокращения чисел по знакам:

1.Оставление k точных знаков от начала чисел (умножение, деление),

2.Оставление k точных знаков после знака дробности (сложение, вычитание).

Использование первого способа при смешанном вычислении подразумевает использование у всех чисел одинакового количества знаков от начала чисел, в т.ч. при сложении и вычитании. Так же обстоит дело и со вторым способом, только в этом случае у всех чисел используется одинаковое количество знаков после знака дробности, даже при умножении и

37

Gorozhankin Alexey Anatolievich (alias − Galan) Russia Samara 2004

делении. Естественно, в обоих случаях нарушаются правила оставления знаков: в первом случае – при сложении и вычитании, во втором – при умножении и делении. У каждого из данных способов существуют свои достоинства и недостатки.

Достоинства первого способа над вторым:

1.Используются основные числовые характеристики какого-то одного числового уровня,

2.Легче поддается проектированию погрешностей вследствие использования какого-то одного значения погрешности или точности,

3.Как правило, обладает большей точностью.

Достоинства второго способа над первым:

1.Более привычен, т.к. в данный момент используется повсеместно,

2.Более простой.

Если какой-либо расчет состоит из одинаковых по характеру видов простейших вычислений, например, только из умножения и деления, то нужно использовать первый способ, или только из сложения и вычитания – то второй способ, но как быть, если в расчете встречаются различные по характеру виды простейших вычислений? В этом случае возникает необходимость в использовании сразу двух способов, что естественно, неприемлемо по причине их разной структуры. Для разработки универсального способа оба способа придется модифицировать таким образом, чтобы при

38

Gorozhankin Alexey Anatolievich (alias − Galan) Russia Samara 2004

переходе от одного вида простейших вычислений к другому не возникало нестыковок между ними.

Как известно, по правилам элементарной математики сначала выполняют умножение и деление, т.е. оставляют k знаков от начала числа, затем выполняют сложение и вычитание, при этом нужно оставлять k знаков после знака дробности. Но после выполнения первых основных действий образуются числа с разным количеством знаков после знака дробности, поэтому перед выполнением сложения или вычитания необходимо выполнить выравнивание этих знаков по следующему правилу:

Числа округляют до того количества знаков после знака дробно-

сти, которое имеет самое наибольшее по модулю число.

Таким образом, рассмотрен переход от умножения и деления к сложению и вычитанию, а вот проблем нестыковки при обратном переходе в пределах одного расчета с использованием одного числового уровня как таковых нет, ведь в любом случае будет получаться одно и тоже количество знаков от начала чисел, что наглядно показано в примере 12.

39

Gorozhankin Alexey Anatolievich (alias − Galan) Russia Samara 2004

Пример 12

Полученные числа Апр

835.1

1.036

95.08

0.1839

Наибольшее число – 835.1

Полученные числа Впр

0.007888 0.5126 0.001449 0.0001946

Наибольшее число – 0.5126

Апр = 835.1 + 1.0 + 95.1	+ 0.2 = 931.4
Впр = 0.0079 + 0.5126 + 0.0014 + 0.0002 = 0.5221
Zпр = Апр · Впр = 931.4 · 0.5221	= 486.28394 ≈ 486.3
Приме-	чание:

в примере использовалось C-округление.

В результате умножения и деления были получены числа для формул

Апр и Впр. В формуле Впр хоть и использовались числа меньшей величины,

чем в формуле Апр, тем не менее, всегда хотя бы одно число (самое наи-

большее) будет иметь неизменное количество знаков как до операции выравнивания знаков, так и после нее, т.к. оно не подлежит округлению. Поэтому нестыковки оставления знаков у чисел при переходе от сложения и вычитания к умножению и делению не существует. Но бывают такие случаи, когда по каким-то причинам отдельные части расчета подсчитаны с различной точностью, т.е. с использованием различного количества знаков от начала числа.

40