Граничные: условия в электростатическом поле

На границе двух различных сред векторы поля должны удовлетворять определенным условиям, которые называются граничными.

Рассмотрим границу двух непроводящих сред, диэлектрические проницаемости которых равны ε1 ε2 . Пусть на границе этих сред имеется свободный заряд с поверхностной плотностью σ. Проведем замкнутую цилиндрическую поверхность S так, чтобы одна ее половина была расположена в первом диэлектрике, другая во втором. По теореме Гаусса поток вектора электрической индукции будет равен зарядам, которые находятся внутри объема, огра­ниченного замкнутой поверхностью S:

Представим поток вектора D в виде суммы трех потоков:

Если площадка ∆S невелика, то можно считать, что во всех точках этой площадки вектор D имеет одну и ту же величину, тогда

Если высоту цилиндра уменьшать так, чтобы площадки ΔS стремились к границе между диэлектриками, то поток через боковую поверхность будет стремиться к нулю. В пределе он обратится в нуль, и тогда Dln∆S—D2n∆S = σ∆S. После сокращения на ∆S мы получим первое граничное условие:

или

Нормальная составляющая вектора электрической индукции на границе двух непроводящих сред претерпевает скачок, равный поверхностной плотности свободных зарядов, распределенных на границе.

Если σ = 0, то

Нормальная составляющая вектора D на границе непрерывна.

Для получения второго граничного условия проведем замкнутую линию L так, чтобы одна ее часть находилась в первом диэлектрике, другая — во втором. Зададимся направлением обхода по часовой стрелке и составим циркуляцию вектора напряженности по контуру 1-2-3-4. В электростатическом иоле циркуляция вектора Е равна нулю.

Представим циркуляцию в виде четырех линейных интегралов:

Если длина отрезка ∆1 невелика, то вектор Е можно считать одинаковым на всем отрезке. Тогда

Если отрезки 2-3 и 4-1 постепенно уменьшать так, чтобы в пределе они стали равными 1улю, а отрезки ∆1 совпали с граничной поверхностью, то остальные два интеграла обратятся в нуль и E1τ∆l — E2τ∆l = 0. После сокращения на ∆1 получим второе граничное условие:

На границе двух непроводящих сред касательные составляющие вектора напряженности электрического поля равны. Надо отметить, что на поверхности раздела двух сред потенциал непрерывен φ1=φ

Если одна из сред проводящая, то граничные условия несколько изменятся. В проводящей среде векторы поля равны нулю, а потенциал всех точек проводника, один и тот же. Пусть первая среда диэлектрик с проницаемостью ε, вторая — проводник; тогда граничные условия запишутся следующим образом;

3. Метод зеркальных изображений

Если электрические заряды расположены вблизи границы двух или нескольких разнородных сред, то векторы поля можно определить, применив искусственный метод расчета, который носит название метода зеркальных изображений. Идея метода заключается в том, что вместо неоднородной среды рассматриваются среды однородные, влияние же неоднородности учитывается введением фиктивных зарядов. Определив векторы поля от совместного действия этих зарядов, записывают граничные условия основной задачи и, пользуясь ими, находят величину введенных фиктивных зарядов и искомые векторы поля.

Пример 1. Заряд Q расположен в диэлектрике с проницаемостью ε на расстоянии d от проводящей плоскости .Требуется определить векторы поля в диэлектрике.

Граничным условием для рассматриваемой задачи является равенство нулю касательной составляющей напряженности электростатического поля на проводящей поверхности. Покажем, что поле двух зарядов, заданного Q и фиктивного Q1, равноудаленных от граничной поверхности, т. е. отстоящих друг от друга на расстоянии 2d, и расположенных в однородном диэлектрике с проницаемостью ε, такое же, как и исследуемое поле. Величина заряда Q1 определится из граничного условия. В области 1 заряд и среда такие же, как и в основной задаче. При одинаковых граничных условиях, по теореме единственности решения уравнений поля, векторы поля в обеих задачах должны быть одинаковыми. На плоскости хОу напряженность поля двух точечных зарядов по

По условию касательная составляющая Eгр равняется нулю, т. е.

Следовательно, Q1 = — Q. Фиктивный заряд должен быть равен заданному по величине и иметь противоположный знак.

В любой точке пространства над плоскостью хОу, т. е. в объеме, занятом полем,

Плотность поверхностных зарядов, индуцированных на граничной плоскости

Можно показать, что весь заряд, индуцированный на граничной поверхности проводящей среды, равен фиктивному заряду. Для этого надо произведение σ_индdS проинтегрировать по всей плоскости хОу.

Следует заметить, что заряд Q притягивается к проводящей плоскости с силой

В области под плоскостью хОу поля нет, так как среда, заполняющая эту область, проводящая.

Пример 2. Заряд Q расположен вблизи плоскости раздела двух диэлектриков и отстоит от нее на расстоянии d. Проницаемость диэлектрика, в которой находится заданный заряд, равна ε1. Проницаемость второго диэлектрика ε2. Требуется определить напряженность электростатического поля и потенциал в обоих диэлектриках. На плоскости раздела должны иметь место следующие соотношения: Е1τ = E2τ; ε1E1n=ε2Е2n. Второе соотношение справедливо в том случае, когда на поверхности раздела двух диэлектриков нет свободных зарядов. Решение рассматриваемой задачи можно свести к решению двух более простых задач. Рассмотрим первую из них.

В однородном диэлектрике с проницаемостью ε1 на расстоянии 2d друг от друга расположены два точечных заряда Q и Q1. Заряды равноудалены от плоскости хОу.. Среда одинаковая, заряд один и тот же. Следовательно, если для произвольной точки, лежащей на плоскости хОу, в обеих задачах вектор Е будет одинаковым, то и в любой точке области 1 на основании теоремы единственности решение уравнений поля должно быть одинаковым. Напряженность и потенциал ноля двух точечных зарядов можно определить методом наложения:

где R1 и R11 - расстояния от зарядов Q и Q1 соответственно до исследуемой точки.

Эти же формулы будут справедливы для основной задачи в области I, если будут выполнены граничные условия. На плоскости xOy:

По условиюЕ1τ = Eτ; E1n=Еn. Рассмотрим вторую, простую задачу. В однородном диэлектрике с проницае­мостью ε2 находится точечный заряд Q2. Он отстоит на расстоянии d от плоскости хОу. на­ходим, что для области II под плоскостью хОу условия обеих задач совпадают. Диэлектрик один и тот же; зарядов нет. Если на плоскости хОу значение вектора Е в обеих задачах будет одинаковым, то по тео­реме единственности Е в любой точке области II определится как на­пряженность поля точечного заряда Q2.

Для точечного заряда

На плоскости xOy

По условию необходимо, чтобы EIIτ=E2τ; EIIn=E2n. Учитывая граничные условия основной задачи , получаем:

Пользуясь этим выражением можно определить неизвестные фиктивные заряды

Знаки зарядов Q и Q2 всегда одинаковые. Знаки зарядов Q1 и Q одинаковые при ε1>ε2 и разные при ε1<ε2 . Если ε1=ε2, то заряд Q=0, заряд Q2=Q. Получается поле точечного заряда в однородной среде. Если вторая среда является проводником, то можно положить ε2=∞, тогда Q1=-Q; Q2=0.

Металлический цилиндр круглого сечения находится в однородном диэлектрике с проницаемостью ε.

Длина цилиндра L намного больше его радиуса а.

Цилиндр несёт на себе положительный заряд Q. Требуется определить напряжённость электрического поля Е и потенциал φ. Внутри цилиндра поля нет: Е=0. Все точки цилиндра имеют один и тот же потенциал. Вне цилиндра поле симметрично и плоскопараллельно.

Изменение характера поля вблизи концов цилиндра можно не учиты­вать, т. е. считать его бесконечно длинным. Напряженность поля Е имеет одинаковые значения в точках, равноудаленных от оси цилиндра. Направление вектора Е нормально к оси. Проведя замкнутую поверхность S так как показано на рисунке, и применив теорему Гаусса, можно записать:

или

Так как

то

а

Чтобы найти потенциал, надо воспользоваться формулой :

Картина поля изображена на рис. 1-17.

Эквипотенциальные поверхности будут цилиндрическими, коак­сиальными с поверхностью проводника. Линии вектора Е представляют собой радиальные прямые.

Как видно из полученных формул, Е и φ меняются при изменении расстояния r от выбранной точки поля до оси цилиндра, а от радиуса цилиндра а не зависят. Это обстоятельство позволяет при исследовании поля заменить металлический цилиндр конечного радиуса заряженной осью, совпадающей с осью проводника. Поле в области r≥a при такой замене останется без изменения, конечно, при условии, что заряд в обоих случаях один и тот же.

В отличии от поля цилиндра поле заряженной оси будет существовать во всём пространстве, причём если линейную плотность заряда принять равной τ=Q/l, то напряжённость электрического поля заряженной оси будет равна:

(1-24)

а потенциал определится из выражения

В случае коаксиального кабеля с внутренним проводником радиуса а и наружным проводником радиуса b выражения Е и φ в диэлектрике между проводами (а≤r≤b) будут такими же, как и в случае одного заряженного цилиндра,

Здесь Q- абсолютное значение заряда одного из проводников кабеля; l- длина кабеля. Если потенциал наружного проводника принять равным нулю, то постоянная интегрирования определится из выражения

и потенциал равен:

В области 0≤r≤a и b≤r≤∞ поля нет.

Поле двух параллельных разноимённо заряженных осей.

Две параллельные оси, отстоящие друг от друга на расстоянии 2х0, несут одинаковый по величине и противоположный по знаку заряд Q. Линейная плотность заряда равна:

Пользуясь методом наложения и формулами для заряженной оси можно записать:

где r1- расстояние от выбранной точки поля до положительно заряженной оси; r2- до отрицательно заряженной оси

Если принять потенциал равным нулю при r1= r2, то постоянная интегрирования обратится в нуль. Картина поля изображена на рисунке. Следы пересечения эквипотенциальных поверхностей с плоскостью хОу — окружности, удовлетворяющие равенству r1/r2 = const = k.

Обозначим х и у координаты произвольной точки М, через которую проходит эквипотенциальная линия. Расстояние от точки М до по­ложительно заряженной оси равно:

От отрицательно заряженной оси расстояние до точки М равно:

Отношение их равно:

После преобразования можно записать равенство

Прибавив к обеим частям которого величину

получим уравнение искомой эквипотенциальной линии:

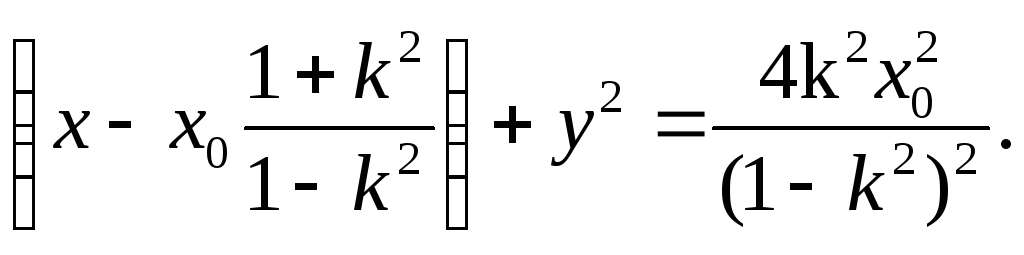
Это уравнение окружности с радиусом

И координатам центра

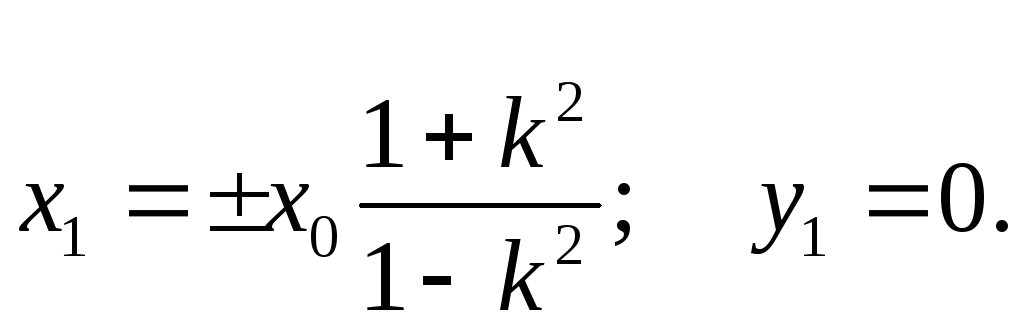
Знак плюс берется при k < 1, т. е. для полупространства с отри­цательно заряженной осью, а знак минус — при k > 1, т. е. для полу­пространства с положительно заряженной осью. В первом случае ок­ружности расположены справа от оси xОу, во втором случае — слева. Величины х0, x1 и R связаны соотношением

в чем можно убедиться, подставив значения х1 и R. Можно показать, что линии вектора Е представляют собой семейство окружностей

которые проходят через заряженные оси. Радиус их равен , а координаты центров х = 0 и y=y1.