6.3. Выявление тренда и построение трендовой модели

Метод проверки разностей средних уровней. Реализация этого метода состоит из четырех этапов.

На первом этапе исходный временной ряд y₁, y₂, y₃, …, y_n разбивается на две примерно равные по числу уровней части: в первой части n₁ первых уровней исходного ряда, во второй — n₂ остальных уровней (n₁ + n₂ = n).

На втором этапе для каждой из этих частей вычисляются средние значения и дисперсии:

; ;

; .

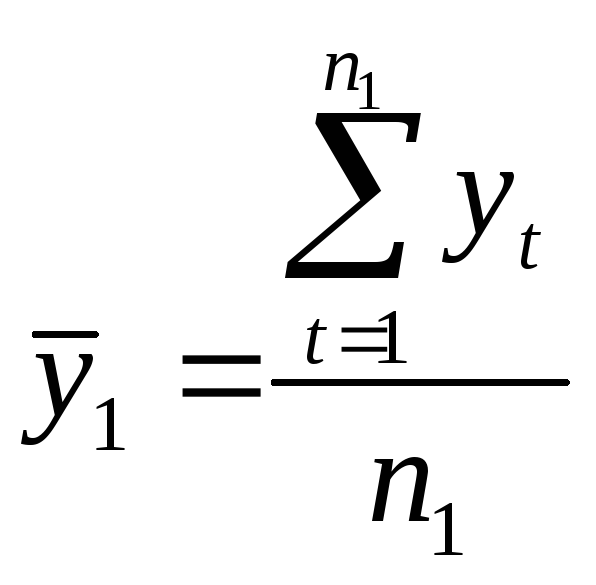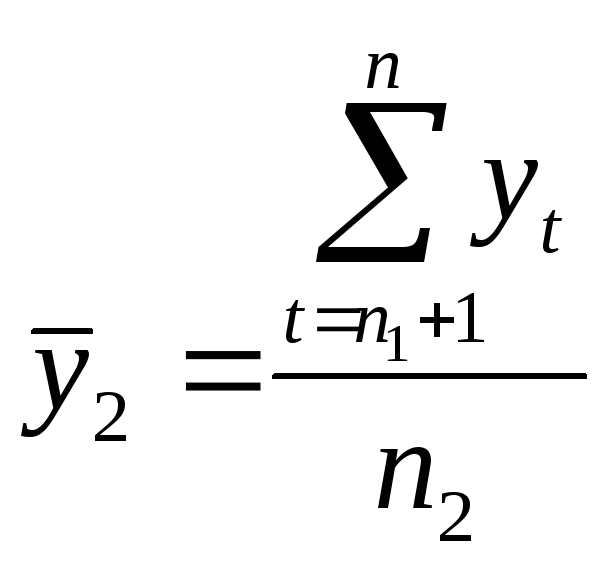Третий этап заключается в проверке равенства (однородности) дисперсий обеих частей ряда с помощью F-критерия Фишера, которая основана на сравнении расчетного значения этого критерия:

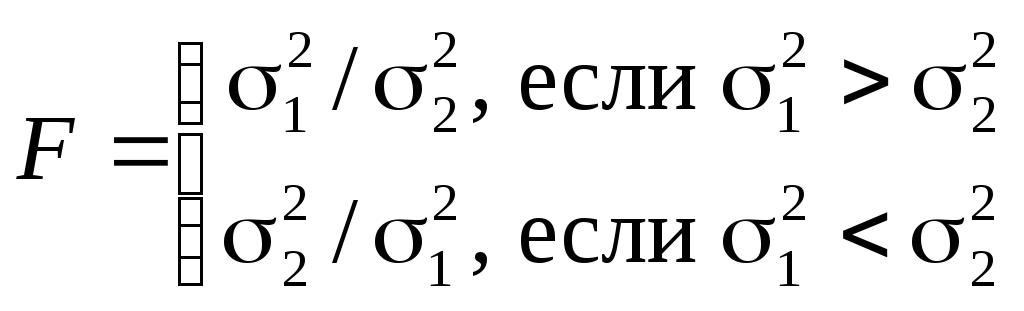
с табличным (критическим) значением критерия Фишера F_ с заданным уровнем значимости (уровнем ошибки) . В качестве , чаще всего берут значения 0,1 (10%-ная ошибка), 0,05 (5%-ная ошибка), 0,01 (1%-ная ошибка). Величина (1–) называется доверительной вероятностью.

Если расчетное значение F_расч меньше критического F_, то гипотеза о равенстве дисперсий принимается и переходят к четвертому этапу. Если F_расч больше или равно F_, гипотеза о равенстве дисперсий отклоняется и делается вывод, что данный метод для определения наличия тренда ответа не дает. Для получения критического значения воспользуйтесь функцией FРАСПОБР(; n₁; n₂).

На четвертом этапе проверяется гипотеза об отсутствии тренда с использованием t-критерия Стыодента. Для этого определяется расчетное значение критерия Стыодента по формуле:

.

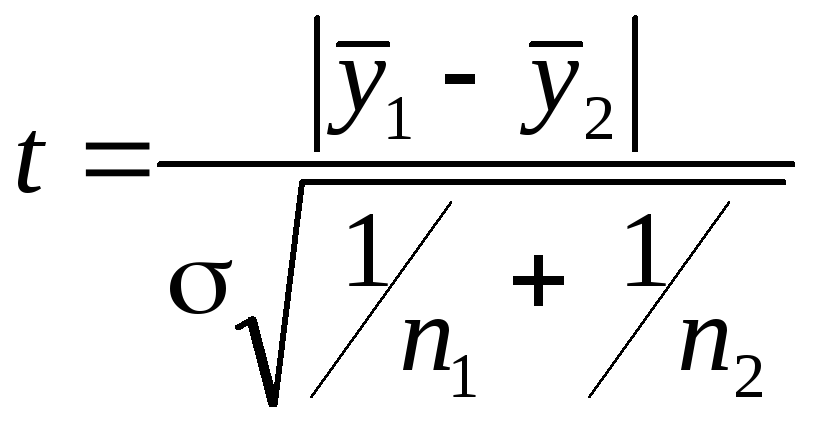где  — среднеквадратическое отклонение разности средних:

.

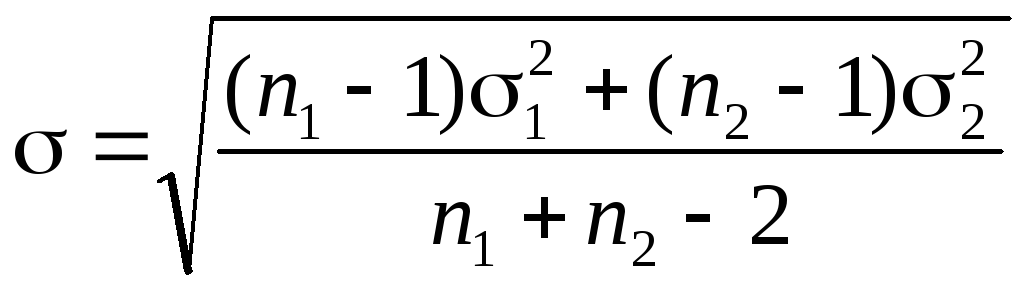Если расчетное значение t меньше критического значения статистики Стьюдента t_ с заданным уровнем значимости , гипотеза принимается, т.е. тренда нет, в противном случае тренд есть. Для получения критического значения воспользуйтесь функцией CTЬЮДРАСПРОБР(; n₁ + n₂ -2). Заметим, что данный метод применим только для рядов с монотонной тенденцией.

Формирование набора моделей, одна из которых будет использована для получения прогноза, происходит на основе интуитивных приемов (таких, например, как анализ графика ряда динамики), формализованных статистических процедур (исследование приростов уровней), а также содержательного анализа процесса. Предпочтение, как правило, отдается простым моделям, допускающим содержательную интерпретацию. К числу наиболее простых относятся линейные модели роста:

(6.1)

где a₀ и a₁ параметры модели, а t = 1, 2, …, n.

Рассмотрим оценку параметров модели по методу, сводящемуся к поиску таких значений a₀ и a₁, при которых сумма квадратов отклонений эмпирических (опытных) данных от рассчитанных по модели (6.1) является наименьшей – метод наименьших квадратов (МНК). Математически критерий такой оценки параметров записывается в виде

Для нахождения минимума функции двух переменных следует взять частные производные по a₀ и a₁, а затем приравнять их к нулю.

В результате получаем систему нормальных уравнений

Решая эту систему, получим формулы для нахождения параметров а₀ и а₁:

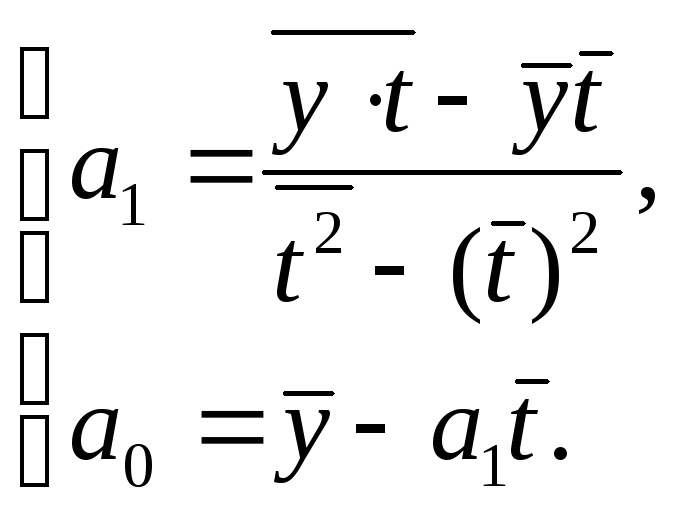(6.2)

6.4. Проверка адекватности моделей

Важным этапом прогнозирования социально-экономических процессов является проверка адекватности (соответствия) модели реальному явлению. Для ее осуществления исследуют ряд остатков , то есть отклонений расчетных значений от фактических. Если модель выбрана правильно, то для остатков характерны:

1. случайный характер значений. Проверяется с помощью критерия поворотных точек;

2. отсутствие автокорреляции (самозависимости). Остатки должны быть независимыми друг от друга. Проверяется с помощью критерия Дарбина – Уотсона;

3. нормальный закон распределения. Проверяется с помощью R/S – критерия;

4. математическое ожидание остатков должно быть равно нулю и дисперсия остатков должна быть неизменна во времени. Проверяется с помощью t– критерия Стьюдента

Рассмотрим перечисленные требования подробнее.

1. Для проверки условия случайности возникновения отдельных отклонений от модели часто используется критерий, основанный на поворотных точках. Уровень последовательности E_i считается максимумом, если он больше двух рядом стоящих уровней, т.е. E_{i -1} < E_i > E_{i +1} и минимумом, если он меньше обоих соседних уровней, т.е. E_{i -1} > E_i < E_{i +1}. В обоих случаях E_i считается поворотной точкой; общее число поворотных точек для остаточной последовательности E_i обозначим через p.

В случайной выборке математическое ожидание числа точек поворота p и дисперсия ²_p выражаются формулами:

Критерием случайности с 5%-ным уровнем значимости, т.е. с доверительной вероятностью 95%, является выполнение неравенства , где квадратные скобки означают целую часть числа. Если неравенство выполняется, то с вероятностью 95% делаем вывод о случайном характере ряда остатков. Если это неравенство не выполняется, модель считается неадекватной.

2. Проверка независимости значений уровней случайной компоненты, т.е. проверка отсутствия существенной автокорреляции в остаточной последовательности может осуществляться по ряду критериев, наиболее распространенным из которых является d-критерий Дарбина—Уотсона. Необходимо вычислить расчетное значение 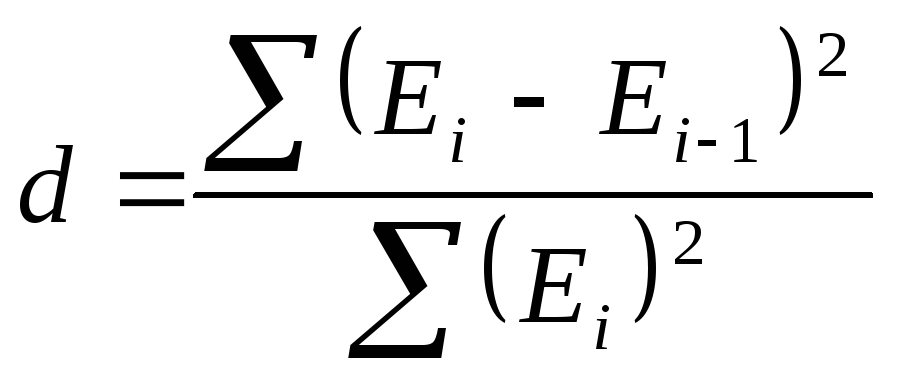, где Е_i – i- тый уровень остаточной последовательности (i=1..9). Теоретическое обоснование применения этого критерия обусловлено тем, что в динамических рядах как сами наблюдения, так и отклонения от них расположены в хронологическом порядке.

Значение d может располагаться в пределах от 0 до 4. При отсутствии автокорреляции значение d примерно равно 2. При полной автокорреляции – 0 или 4. Следовательно, оценки, получаемые по этому критерию, являются не точечными, а интервальными. Верхние (d₂) и нижние (d₁) критические значения, позволяющие принять или опровергнуть гипотезу об отсутствия автокорреляции, зависят от количества уровней динамического ряда и числа независимых переменных модели. Они приведены в задании к контрольной работе. При сравнении расчетного значения d с табличным могут возникнуть следующие ситуации:

• d₂<d<2 – ряд остатков не коррелирован;

• d<d₁ – остатки содержат автокорреляцию;

• d₁<d<d₂ – область неопределенности, когда нет оснований ни принять, ни отвергнуть гипотезу о существовании автокорреляции. Необходимо применять другой критерий;

• d>2, то это свидетельствует об отрицательной связи, и его надо преобразовать по формуле d' = 4-d и посмотреть, в какой из трех первых интервалов попадает значение d'.

1)		2)		3)		4)
–		?		+
критерий не выполняется		область неопределенности		критерий выполняется		отрицательная связь
0		d1		d2		2	4
Делаем вывод о наличии автокорреляции		Применяем другой критерий Если |r1| < 0,36, то автокорреляция отсутствует, иначе присутствует.		Делаем вывод об отсутствии автокорреляции		Вычисляем d'=4-d и смотрим, в какой из интервалов 1), 2) или 3) попало d'.

Установив наличие автокорреляции остатков, надо улучшать модель.

Если же ситуация оказалась неопределенной (d₁<d<d₂), применяют другие критерии. В частности, можно воспользоваться первым коэффициентом автокорреляции: 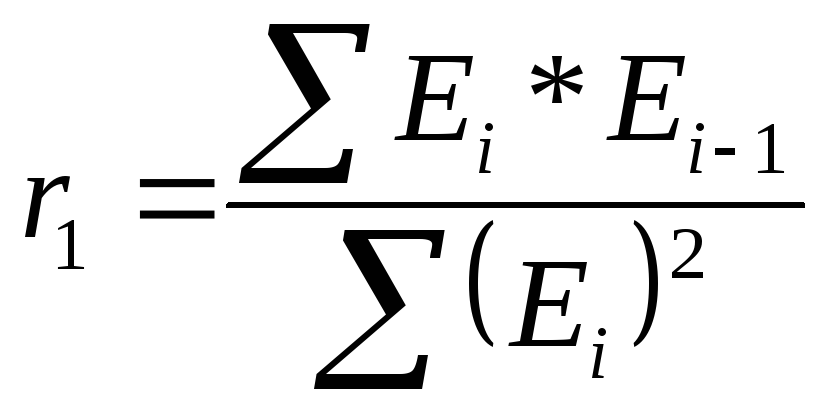. Для суждения о наличии или отсутствии автокорреляции в исследуемом ряду расчетное значение коэффициента r₁ сравнивают с критическим для 5%-го уровня значимости (в нашем случае можно взять в качестве r_крит = 0,36). Если |r₁| меньше критического значения, то делается вывод об отсутствии автокорреляции в ряду остатков. Если |r₁| больше критического значения, то с вероятностью 0,95 делают вывод о наличии автокорреляции.

3. Проверка гипотезы о нормальном распределении остаточной последовательности по R/S_E – критерию. В нашем случае R = E_max ‑ E_min, где E_max и E_min соответственно максимальный и минимальный уровни ряда остатков; 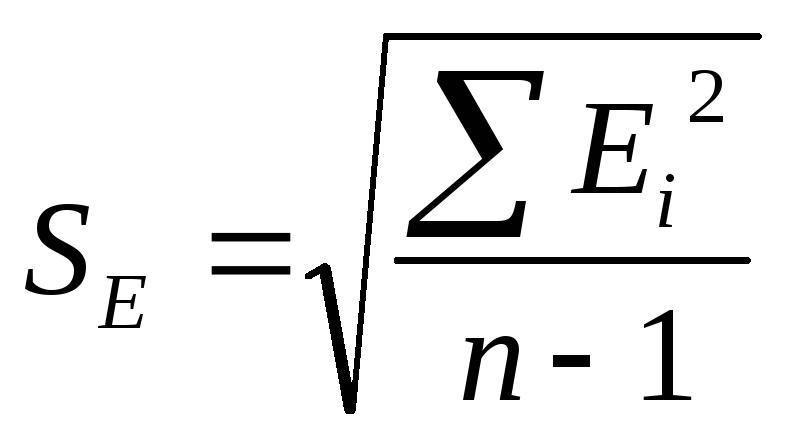. Вычисленное значение R/S_E-критерия сравнивается с критическими нижней и верхней границами данного отношения. Критические границы приведены в задании. Если значение R/S_E попадает в интервал между критическими границами, то с заданным уровнем значимости гипотеза о том, что остаточная последовательность распределена по нормальному закону, принимается; в противном случае эта гипотеза отвергается.

4. Проверка гипотезы о равенстве математического ожидания случайной компоненты нулю на основе t ‑ критерия Стьюдента. Расчетное значение этого критерия задается формулой где — среднее арифметическое значение уровней остаточной последовательности E_t; S_E — стандартное (среднеквадратическое) отклонение для этой последовательности. Если расчетное значение t меньше критического значения t_,v статистики Стьюдента с заданным уровнем значимости  и числом степеней свободы v=n-1, то гипотеза о равенстве нулю математического ожидания случайной последовательности принимается; в противном случае эта гипотеза отвергается и модель считается неадекватной. Для получения критического значения t_,v воспользуйтесь встроенной функцией Excel CTЬЮДРАСПРОБР(;v);

Если ВСЕ четыре вышеперечисленные критерии дают положительный ответ, делается вывод о том, что выбранная модель является адекватной реальному ряду экономической динамики. Только в этом случае ее можно использовать для построения прогнозных оценок. В противном случае модель надо улучшать.