
- •Partea I şirul de experimente independente lucrare de laborator nr. 1 Formula Bernulli. Teorema limită locală a lui Moivre – Laplace
- •Lucrare de laborator nr. 2 Aplicarea Teoremei Integrale Moivre-Laplace. Teorema lui Bernulli.
- •Probleme tipice care conduc la aplicarea teoremei lui Moivre-Laplace.
- •Lucrare de laborator nr. 3 Distribuţia/repartiţia Poisson ca aproximare a distribuţiei binomiale.
- •Anexă b, Funcţia de repartiţie normală normată Laplace (n(0,1))
- •Valorile funcţiei
- •Anexa c. Repartiţia Poisson
Lucrare de laborator nr. 2 Aplicarea Teoremei Integrale Moivre-Laplace. Teorema lui Bernulli.
3°
Teorema
integrala a lui Moivre-Laplace.
Fie ca se face un sir de experimente independente, astfel ca in
fiecare experiment probabilitatea de realizare a evenimentului A
este p. Daca
sau
pentru orice interval
E
usor de inteles ca
4°
Teorema
locala a lui Moivre-Laplace. Fie
unde
Aceasta
teorema ne da o formula asimptotica, prin inlermediul careia pulem
aproxima formula
lui Bernuli/repartitia
binomiala prin cea normala
cand
n
este
suficient de mare:
![]() este
numarul de aparitii ale lui A in primele n experimente, atunci
pentru orice
este
numarul de aparitii ale lui A in primele n experimente, atunci
pentru orice
![]() avem
avem![]()
![]()
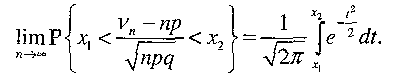
![]() unde
unde
![]() este
numarul de aparitii ale evenimentului A
in
experiment de rang i.
este
numarul de aparitii ale evenimentului A
in
experiment de rang i.![]() numarul
de apariţii ale unui eveniment A in n experimente indepetidente şi
p probabilitatea acestui eveniment in fiecare experiment. Atunci,
pentru
numarul
de apariţii ale unui eveniment A in n experimente indepetidente şi
p probabilitatea acestui eveniment in fiecare experiment. Atunci,
pentru
![]()
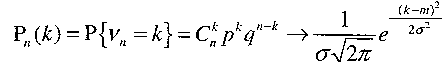
![]()
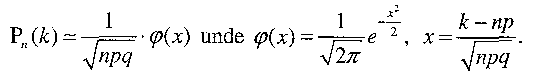
Într-o serie n de experimente independente, în fiecare din care evenimentul A apare cu una şi aceeaşi probabilitate p (0 <p <1), în conformitate cu teorema Moivre-Laplace este adevărată egalitatea:
, (2.1)
unde k- numărul de realizări ale evenimentului A, în rezultatul a n experimente; Φ (x) - Funcţia Laplace definită prin integrală.
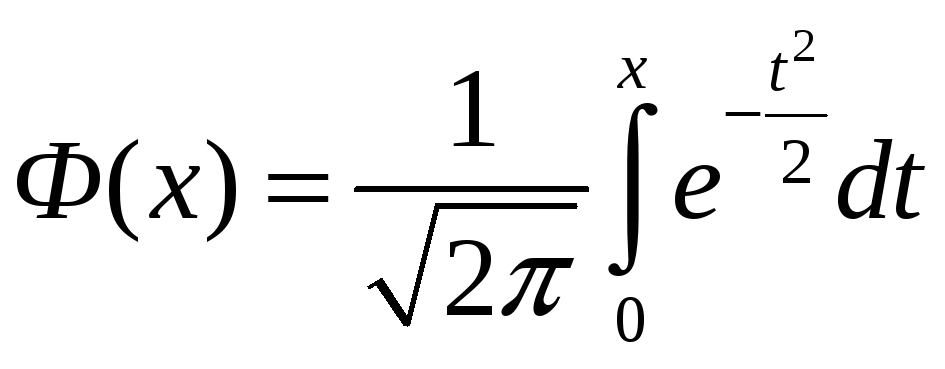 (2.2)
(2.2)
Aplicînd teorema integrală a lui Moivre-Laplace pentru estimarea probabilităţii inegalităţii
![]()
unde ε – constantă pozitivă, vom obţine
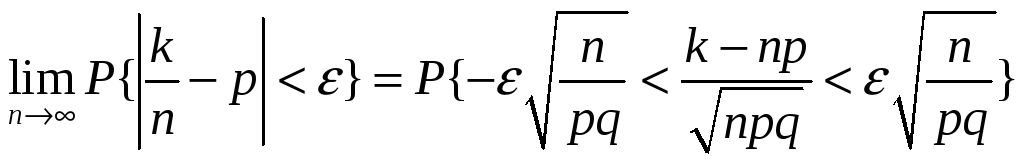
şi în virtutea Teoremei Moivre-Laplace vom regăsi teorema lui Bernulli
(2.3)
2°
Teorema
lui
Bernoulli.
Fie
sau, echivalent,
Sa
consideram variabila aleatoare
Evident ca
Deoarece
Atunci, in virtutea teoremei
lui Cebasev, avem
In concluzie, putem spune ca
teorema lui Bernoulli este o consecinta a teoremei lui Cebaşev.
Acest rezultat clasic poate
fi formulat si in felul urmator:
şirul
In
condifiile teoremei lui Bernoulli, E. Borel in 1909 a aratat un
rezultat mai profund şi anume ca
Teorema lui Bernoulli
explica stabilitatea frecventei relative pentru un numar mare de
experimente, iar probabilitatea se dezvaluie ca un punct de
condensare a frecventelor relative.
Aceasta
teorema sintetizeaza legatura dintre frecventa relativa si
probabilitate, care sta la baza axiomatizarii moderne a teoriei
probabilitatilor.
![]() numarul
de aparitii ale unui eveniment A in
n experimente independente şi p - probabilitatea de realizare a lui
A in fiecare experiment.
Atunci, pentru orice
numarul
de aparitii ale unui eveniment A in
n experimente independente şi p - probabilitatea de realizare a lui
A in fiecare experiment.
Atunci, pentru orice
![]()
![]()
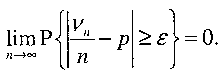
![]() care
ia ca valori numarul de realizari ale evenimentului
A
in
experimentul de rang i
- deci repartitia sa este
care
ia ca valori numarul de realizari ale evenimentului
A
in
experimentul de rang i
- deci repartitia sa este![]()
![]()
![]() are
aceeasi repartitie ca si
are
aceeasi repartitie ca si
![]() rezulta:
rezulta: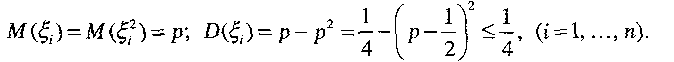
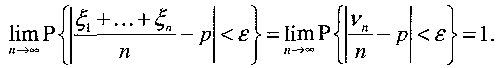
![]() de
variabile aleatoare converge in probabilitate catre probabilitatea p
(in
aceasta formulare cuvîntul „probabilitate" intervine in doua
sensuri diferite): Vom scrie
de
variabile aleatoare converge in probabilitate catre probabilitatea p
(in
aceasta formulare cuvîntul „probabilitate" intervine in doua
sensuri diferite): Vom scrie
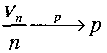 .
.![]()
