3. Методы решения матричных игр

3.1. Графический метод решения

Рассмотрим графический метод нахождения решений игры. Этот метод очень просто применять к играм, имеющим матрицы 2хn или mх2. Его можно также применять к играм, имеющим матрицы 3хn и mх3, но он не пригоден для матриц mxn, когда m и n больше 3.

Поясним этот метод на примере решения игр 2хn [7].

Пример 3.1. Рассмотрим платежную игру с матрицей

Здесь игрок I имеет две чистые стратегии (по строкам), а игрок II три чистые стратегии (по столбцам). Если игрок I применяет смешанную стратегию, а игрок II – свою первую чистую, то ожидаемый платеж игроку I будет

Аналогично, если игрок II применит свою чистую стратегию II? То ожидаемый платеж игроку I равен

,

а если игрок II применит чистую стратегию 3 , то ожидаемый платеж игроку I равен

.

Проведем три прямые, соответствующие этим платежам.

При каждом выборе игроком I стратегии x он может быть уверен, что получит по крайней мере наименьшую из ординат трёх прямых, соответствующих x.

Таким образом, для игрока I выбрать оптимальное x – это значит выбрать такое х, при котором наименьшая из трех ординат возможно больше. Следовательно, цена игры в приведенном примере находится следующим образом: берём максимальную ординату выпуклого множества, которое ограничено сверху прямыми линиями. Такой же способ применяется для любой игры с матрицей порядка 2хn. Для игры с матрицей порядка mх2 графическое построение аналогично, но в этом случае цена игры равна минимальной ординате выпуклого множества, ограниченного снизу прямыми линиями. Мы можем в этом частном случае найти оптимальную стратегию игрока I (на рисунке видно, что игрок имеет только одну оптимальную стратегию) и цену игры, решив совместно уравнения

Проделав вычисления, мы находим, что оптимальная стратегия игрока I и цена игры равна . Дале , из рисунка видно, что первая стратегия игрока II не войдет в его оптимальную смешанную стратегию. Значит оптимальную смешанную стратегию игрока II мы можем найти из матрицы

.

Отсюда находим, что оптимальная стратегия игрока II равна .

В случае, если игрок имеет много оптимальных стратегий (на рисунке это выразится в том, что один из графиков будет параллелен оси) это будет естественное обобщение отрезка прямой на плоскости. Тогда оптимальной стратегией будет любая пара, принадлежащая этому отрезку.

Таким образом, найдено графическое решение 2х3 игры.

3.2. Прямое решение

Вообще, любую матричную игру можно решить путём решения системы неравенств. Но с увеличением числа чистых стратегий игроков размерность растет, а следовательно, значительно увеличивается и объем вычислений. Поэтому, в первую очередь следует уменьшить размерность матрицы, исключив строго доминируемые стратегии. Затем следует проверить выполнение равенства минимаксов. Если равенство минимаксов выполняется, то это означает, что игроки имеют чистые оптимальные стратегии (наличие седловой точки в чистых стратегиях). Игрок I здесь имеет чистую максиминную, а игрок II чистую минимаксную стратегию.

В противном случае хотя бы у одного игрока оптимальные стратегии будут смешанными.

Рассмотрим пример

Пример 3.2. [1] Пусть Г = <х, у, Н> где х={1,2,3,4}, у={1,2,3,4},а функция выигрыша Н задана следующим образом:

,

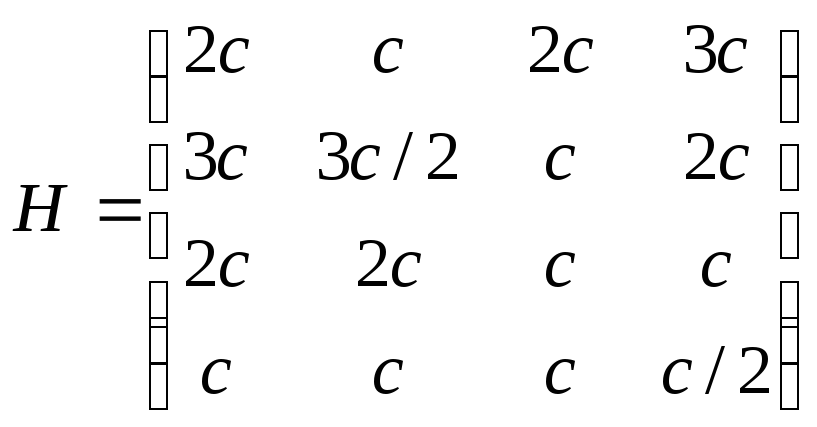где с > 0.

Прежде всего заметим, что достаточ­но решить игру Г¹ =<х, у, Н¹> , где Н¹ = Н/с. В матрич­ной форме игра Г¹ определяется матрицей выигрышей

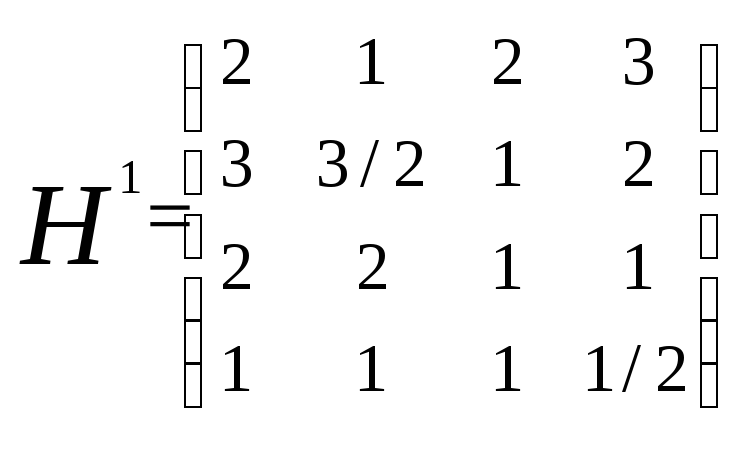
Элементы четвертой строки этой матрицы не больше соответствующих элементов третьей строки, и поэтому третья стратегия игрока I доминирует четвертую. Кроме того, элементы первого столбца матрицы Н¹ не меньше соответствующих элементов второго столбца. Следователь­но, вторая стратегия игрока II доминирует его первую стратегию.

Далее, можно утверждать (раздел 2.7), что всякое решение игры Г² = <х \{4}, y \{1}, H¹) является решением игры Г¹. В матричной форме игру Г² можно представить мат­рицей

,

в которой i-й строке матрицы соответствует i-я страте­гия, а j-му столбцу — j + 1-я стратегия. Очевидно, что элементы второй строки этой матрицы не меньше полу­суммы соответствующих элементов первой и третьей строк. Следовательно, вторая стратегия игрока II доминируется смешанной стратегией, которая с равными ве­роятностями использует первую и вторую стратегии этого игрока. Кроме того, элементы третьего столбца матрицы H² не меньше соответствующих элементов вто­рого столбца. Это значит, что стратегия под номером 3 доминирует стратегию под номером 4. Всякое решение игры Г³ = <x\{4, 2}, y\{1,4}, H²> является решением игры Г², а значит, и иг­ры Г¹.

Игра Г³ определяется матрицей:

в которой первая строка соответствует стратегии под но­мером 1, вторая — стратегии под номером 3 первоначальной игры, а второй и третий столбцы соответствуют стра­тегиям 2 и 3 первоначальной игры. Матрица H³ не имеет седловой точки, так как не выполнено равенство минимаксов, а игра Г³ не имеет решения в чистых стратегиях, т. е. оптимальные стратегии игроков являются смешанными. Эти стратегии легко найти из анализа структуры матри­цы H³. Поскольку матрица H³ симметрична, можно пред­положить, что игроки в оптимальной стратегии исполь­зуют свои чистые стратегии с равными вероятностями.

Действительно, если игрок I применяет стратегию, смешивающую с равными вероятностями первую и вто­рую строки матрицы игры Г³, или (что то же самое) вы­бирает с равными вероятностями стратегии 1 и 3, то при применении любой из двух чистых стратегий игроком II математическое ожидание выигрыша игрока I будет рав­но либо (1/2)1+ (1/2)2 = 3/2, либо (1/2)2 +(1/2)1 =3/2. Аналогично, если игрок II использует свои чистые стра­тегии 2 и 3 с равными вероятностями, то математиче­ское ожидание его проигрыша будет равно 3/2. Следова­тельно, указанные стратегии являются оптимальными в игре Г³, а величина 3/2 — значением игры Г³. Из преды­дущего следует, что эти стратегии оптимальны и в Г¹.

Таким образом, стратегия X* = (1/2, 0, 1/2, 0) явля­ется оптимальной стратегией игрока I, стратегия У* = (0, 1/2, 1/2, 0)—оптимальной стратегией игрока II в игре Г¹, а значение игры Г¹ равно 3/2. В силу теоремы 1.11 решением игры Г будет тройка (X*, У*, Зс/2).

При решении примера нам пришлось столкнуться с решением 2 X 2-игры. Сначала мы догадались, как выг­лядит решение, а потом проверили, что оно действитель­но является решением. Оказывается любую 2 X 2-игру можно решить по следующей стандартной схеме.

В общем виде 2 X 2-игра определяется матрицей

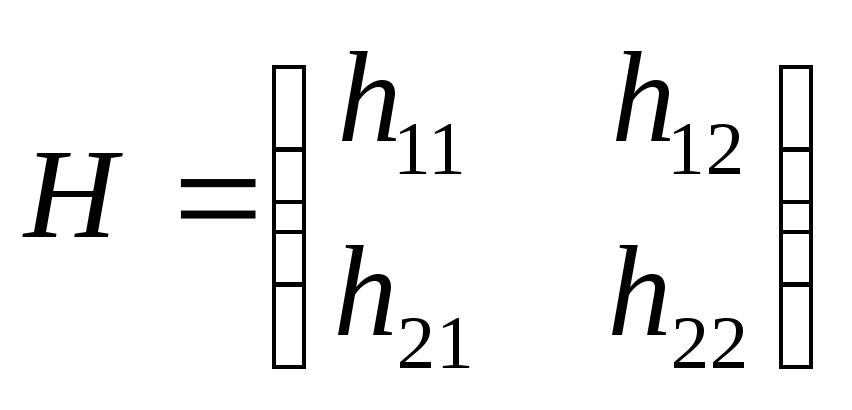
Прежде всего, необходимо проверить выполнение ра­венства минимаксов. Если оно выполняется, то игра имеет решение в чистых стратегиях, причем опти­мальными стратегиями игроков I и II соответственно будут чистая максиминная и чистая минимаксная стра­тегии. Если же игра с матрицей выигрышей H не имеет решения в чистых стратегиях, то оба игрока имеют лишь такие оптимальные стратегии, которые используют все свои чистые стратегии с положительными вероятностями. Действительно, в противном случае один из игроков (скажем, игрок I) имеет чистую оптимальную стратегию, а другой — только смешанные. Не ограничивая общ­ности, можно считать, что оптимальной стратегией игро­ка I является выбор с вероятностью единица первой строки. Далее h₁₁= h_l2 = v и матрица имеет вид:

Легко видеть, что для матриц такого вида одна из стра­тегий игрока II является доминируемой. Следовательно, по теореме 1.11 этот игрок имеет чистую оптимальную стратегию, что противоречит предположению.

Пусть Х* = - оптимальная стратегия игрока I. Так как игрок II имеет смешанную оптимальную стратегию, то получим H(X*_t j) = v, j = 1, 2, или, в подробной записи,

(3.1)

Отсюда следует, что при v 0 столбцы матрицы H не могут быть пропорциональны с коэффициентом про­порциональности, отличным от единицы. Если же коэф­фициент пропорциональности равен единице, то матрица Н принимает вид

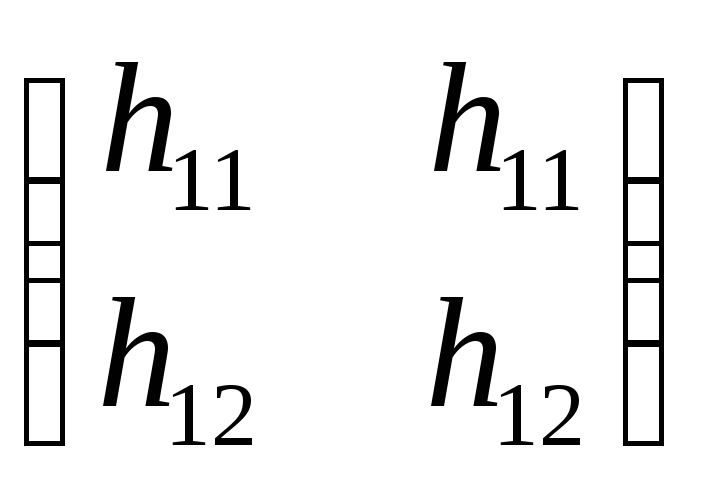
и игрок I имеет чистую оптимальную стратегию (он вы­бирает с вероятностью единица ту из строк, элементы ко­торой не меньше соответствующих элементов другой), что противоречит предположению. Следовательно, если v 0 и игроки имеют только смешанные оптимальные стратегии, то определитель матрицы Н отличен от нуля. Из этого следует, что система уравнений (3.1) имеет единственное решение. Решая ее, находим

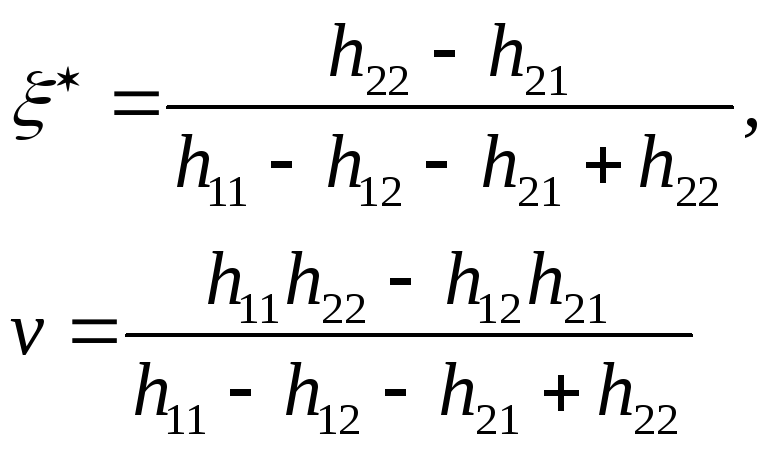(3.2)

Аналогичные рассуждения приводят иле к тому, что оптимальная стратегия игрока II Y * = (*, 1 - *) удов­летворяет системе уравнений:

(3.3)

откуда (3.4)

Таким образом, для решения матричной 2 Х 2-игры необходимо сначала проверить равенство минимаксов, и если оно выполняется, то игроки имеют чистые оптимальные стратегии (игрок I — чистую максиминную, а игрок II — чистую минимаксную). В противном случае следует по формулам (3.2) и (3.3) найти значения, оптимальные стратегии игроков.

В некоторых случаях, когда игра имеет решение в смешанных стратегиях, из анализа структуры матрицы выигрышей можно получить некоторое представление о тех чистых стратегиях, которые должны применяться с положительной вероятностью. Другими словами, иногда можно угадать подмножества х° и у⁰ чистых стратегий, а затем решить систему:

H(X,j) = v, , (3.5)

H(i, Y) = v,

Если решение системы (3.5) удовлетворяет условиям равновесности ситуации, то оно является искомым решением игры Г. В противном случае можно последовательно переби­рать подмножества х° и у⁰, решая соответствующие системы и проверяя каждое решение до тех пор, пока не будет получено решение исходной игры Г. Кроме того, можно ограничиться подмножествами, имеющими равное число элементов, то есть в матричной записи перебрать квадратные подматрицы матрицы выигрышей. Можно показать, что в этом случае обязательно при каких-нибудь х° и у⁰, имеющих по одинаковому числу элементов, решение системы (3.5) будет единственно и является решением игры Г = <х, у. Н>. Выше мы по­казали это для 2 X 2-игр.

Напомним, что рассмотренный метод непосредствен­ного (прямого) решения годится лишь для игр неболь­шого размера и для игр, которые сводятся к таковым отбрасыванием доминируемых стратегий, либо для игр, которые имеют некоторую обозримую аналитическую структуру и для которых можно угадать спектр опти­мальных стратегий. Поэтому если игра сложная, то луч­ше всего для ее решения воспользоваться численными методами линейного программирования (например, симп­лекс-методом).