2. Для несовместных событий вероятность их суммы равна сумме их вероятностей

Р(А+В)= 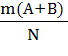= = 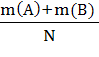+ = Р(А)+Р(В).

3. Для полного набора событий их сумма  достоверное событие, т.е.

Р()= = 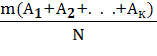= =1.

Отсюда для несовместных событий А и В находим Р(АВ)=0 ввиду отсутствия благоприятных исходов. Далее, учитывая, что А+=Ω, вследствие несовместности события и ему противоположного получаем

Р(А+)=Р(А)+Р()=1 или Р()=1Р(А).

В качестве примера рассмотрим бросание кубика. При условии полной симметрии кубика вероятность выпадения любой его грани равна 1/6. Поэтому для события А=”выпало четное число” из расчета три благоприятных исхода из шести возможных имеем Р(А)=3/6=1/2=0,5.

Если бросать два кубика одновременно, то для события А=”сумма выпавших цифр равна 10” общее количестве исходов равно 66=36, поскольку каждый исход на первом кубике может комбинировать с каждым исходом на втором кубике. Для того, чтобы убедиться в этом дос-

	1 2 3 4 5 6
1 2 3 4 5 6	2 3 4 5 6 7 3 4 5 6 7 8 4 5 6 7 8 9 5 6 7 8 9 10 6 7 8 9 10 11 7 8 9 10 11 12

таточно составить таблицу с перечислением всевозможных исходов с обозначением и цифр, выпавших на первом и втором кубиках соответственно. Из этой таблицы сразу же извлекаются благоприятные исходы в количестве трех штук: (6, 4), (5, 5), (4, 6). Теперь нетрудно посчитать, что Р(А)==. Полученный результат трактуется так,  в реальном эксперименте на каждые 12 испытаний в среднем придется лишь один благоприятный исход.

7 Схемы случайных экспериментов

Многие случайные события моделируются экспериментами с извлечением перенумерованных или разноцветных шаров из урны. Шары можно извлекать с учетом или без учета их номеров. После извлечения шар в урну можно вернуть, а можно этого не делать. Поэтому различают соответствующие схемы выбора, в каждой из которых общее число исходов и благоприятных исходов подсчитывается по-разному.

Сначала посчитаем количество перестановок в совокупности из n перенумерованных шаров. Для выбора первого шара имеется n возможностей. Второй шар может быть выбран уже только n-1 способом и т.д. Поскольку каждый способ выбора первого шара может комбинировать со всеми способами выбора второго шара, то в качестве числа перестановок в группе из n перенумерованных шаров находим

N=n(n-1)(n-2) . . . 3·2·1=n!.

Для произведения последовательности чисел от 1 до n здесь использовано стандартное обозначение n!, которое читается как “n факториал”.