
- •Предел и непрерывность функции одной переменной
- •Введение. Множества и операции над ними
- •Примеры числовых множеств, их стандартные обозначения
- •Пустое множество
- •Включение множеств
- •Равенство множеств
- •Операции над множествами
- •Эквивалентность множеств
- •Мощность множества
- •§ 1. Функция
- •Способы задания функции
- •Аналитический способ задания функции.
- •Табличный способ задания функции.
- •Графический способ задания функции.
- •График функции
- •Обратная функция
- •Основные элементарные функции
- •4) Тригонометрические функции.
- •5) Обратные тригонометрические функции.
- •Суперпозиция функций
- •Классификация функций
- •Задачи к § 1
- •§ 2. Бесконечно малые функции
- •Задачи к §2
- •§ 3. Свойства бесконечно малых функций
- •Задачи к §3
- •§ 4. Бесконечно большие функции
- •Задачи к §4
- •§ 5. Предел функции
- •Односторонние пределы
- •Свойства предела функции
- •Задачи к §5
- •§ 6. Теоремы о вычислении предела функции. Неопределенности
- •Задачи к §6
- •§ 7. Замечательные пределы
- •2) Число . Натуральные логарифмы
- •§ 8. Сравнение бесконечно малых. Эквивалентные бесконечно малые
- •Вычисление пределов степенно-показательных функций
- •Задачи к §8
- •§ 9. Непрерывность функции
- •Второе определение непрерывности
- •Точки разрыва
- •Свойства функций, непрерывных на замкнутом промежутке
- •Задачи к §9
- •Литература
- •Оглавление
§ 7. Замечательные пределы
Устанавливаемые в этом параграфе соотношения позволяют в некоторых случаях раскрывать неопределенности и находить значения пределов.
1) Теорема 7.1. Справедливо соотношение
![]() .
.
Доказательство.
Достаточно рассмотреть
![]() ,
так как
,
так как
![]() .
Обратимся к рис. 7.1. На нем изображена
окружность, радиус которой равен
.
Обратимся к рис. 7.1. На нем изображена
окружность, радиус которой равен
![]() .
Точки
.
Точки
![]() ,
,
![]() ,
,
![]() лежат на этой окружности, причем
лежат на этой окружности, причем
![]() (
(![]() – точка пересечения хорды
– точка пересечения хорды
![]() и радиуса
и радиуса
![]() ).
В точках
).
В точках
![]() и
и
![]() к окружности проведены касательные.
Они пересекаются в точке
к окружности проведены касательные.
Они пересекаются в точке
![]() ,
лежащей на прямой
,
лежащей на прямой
![]() .
.
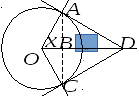
Рис. 7.1.
Из рис. 7.1 очевидны соотношения:
![]() ;
;
![]() ;
;
![]() .
.
Так как
![]() ,
то
,
то
![]() .
.
Разделив все три
части неравенства на
![]() и перейдя к обратным величинам, будем
иметь
и перейдя к обратным величинам, будем
иметь
![]() .
.
Применяя теорему
5.5 о сжатой переменой и учитывая, что по
теореме 6.1
![]() ,
получим
,
получим
![]() .
.
Теорема доказана.
2) Число . Натуральные логарифмы
Рассмотрим
график функции
![]() .
При любом значении
.
При любом значении
![]() (рис. 7.2) он проходит через точку
(рис. 7.2) он проходит через точку
![]() .
Построим касательную
.
Построим касательную
![]() к графику
к графику
![]() в точке
в точке
![]() .
Воспользуемся при этом следующим
определением.
.
Воспользуемся при этом следующим
определением.
Определение
7.1. Касательной
к кривой
![]() в точке
в точке
![]() называется предельное положение секущей
называется предельное положение секущей
![]()
![]() при стремлении точки
при стремлении точки
![]() к точке
к точке
![]() вдоль кривой
вдоль кривой
![]() .
.
Угловой
коэффициент касательной к графику
функции
![]() в точке
в точке
![]() зависит от значения основания логарифма
зависит от значения основания логарифма
![]() .
Из всех значений
.
Из всех значений
![]() выделим то, для которого угловой
коэффициент касательной
выделим то, для которого угловой
коэффициент касательной
![]() .
Это значение обозначим через
.
Это значение обозначим через
![]() .
Последнее является иррациональным
числом:
.
Последнее является иррациональным
числом:
![]() .
Логарифмы по основанию
.
Логарифмы по основанию
![]() называются натуральными
логарифмами
и обозначаются
символом «
называются натуральными
логарифмами
и обозначаются
символом «![]() ».
».
Теорема 7.2. Справедливо соотношение
![]() .
.
Доказательство.
Обратимся к рис. 7.2. Рассмотрим угловой
коэффициент секущей
![]()
![]() .
.

Рис. 7.2.
Угловой
коэффициент касательной (с углом наклона
![]() )
может быть получен как предел углового
коэффициента секущей при
)
может быть получен как предел углового
коэффициента секущей при
![]() ,
то есть при
,
то есть при
![]() .Таким
образом,
.Таким
образом,
![]() .
.
После
замены
![]() получим
получим
![]() .
.
Теорема 7.2 доказана.
3)
Теорема 7.3.
Для
![]() справедливо соотношение:
справедливо соотношение:
![]() .
.
Доказательство.
Введем переменную
![]() ,
откуда
,
откуда
![]() .
Если
.
Если
![]() ,
то
,
то
![]() .
Тогда
.
Тогда
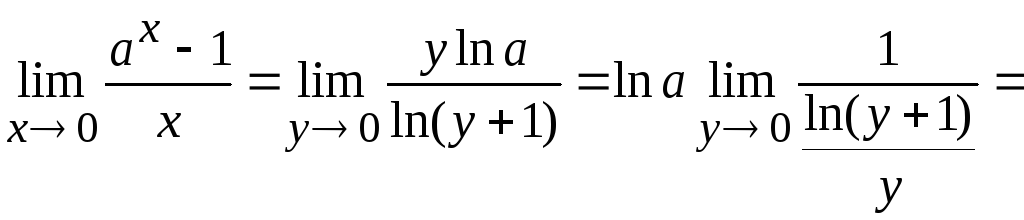
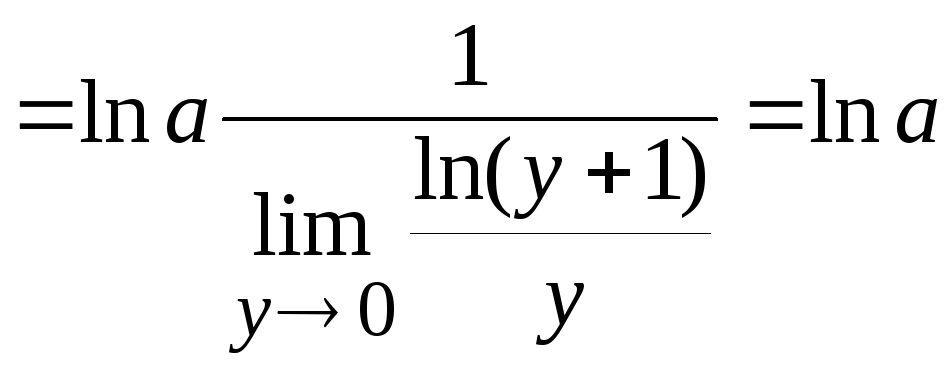 .
.
Теорема 7.3 доказана.
4)
Теорема
7.4. Для
![]() справедливо соотношение:
справедливо соотношение:
![]() .
.
Доказательство.
Будем рассматривать значения
![]() .
Введем переменную
.
Введем переменную
![]() .
Из определения переменной
.
Из определения переменной
![]() следует, что
следует, что
![]() ,
откуда
,
откуда
![]() .
Если
.
Если
![]() ,
то
,
то
![]() .
Умножим числитель и знаменатель дроби,
стоящей под знаком предела, на равные
величины
.
Умножим числитель и знаменатель дроби,
стоящей под знаком предела, на равные
величины
![]() и
и
![]() соответственно и по теореме 6.2 перейдем
к произведению пределов
соответственно и по теореме 6.2 перейдем
к произведению пределов
![]()
![]() .
.
В силу теоремы 7.2
![]() .
.
Теорема доказана.
Пример 7.1. Вычислить предел
![]() ,
,
![]() .
.
Решение.
Имеем неопределенность типа
![]() .
Введем обозначение
.
Введем обозначение
![]() .
В силу теоремы 6.2 если
.
В силу теоремы 6.2 если
![]() ,
то
,
то
![]() .
По теореме 7.1 получим:
.
По теореме 7.1 получим:
![]() .
.
Пример 7.2. Вычислить предел
![]() ,
,
![]() .
.
Решение.
Имеем неопределенность типа
![]() .
Преобразуем выражение под знаком
предела:
.
Преобразуем выражение под знаком
предела:
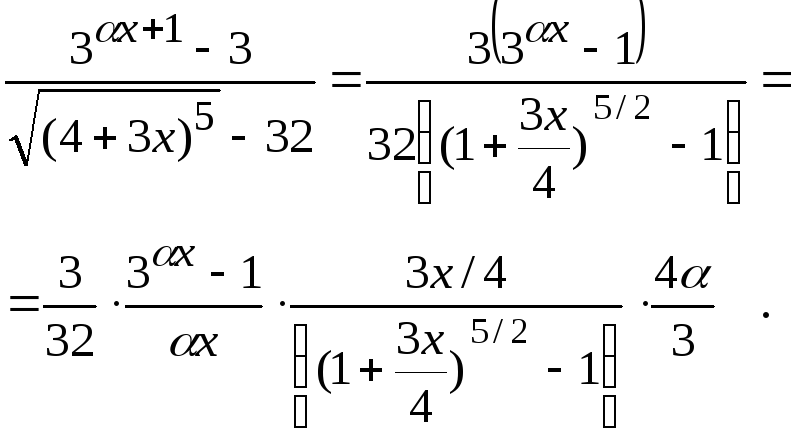
По
теореме 6.2 перейдем к произведению
пределов. Введем обозначения
![]() ,
,
![]() .
По теореме 6.2 если
.
По теореме 6.2 если
![]() ,
то
,
то
![]() и
и
![]() .
Используя теоремы 7.3 и 7.4, получим:
.
Используя теоремы 7.3 и 7.4, получим:
![]()
Пример 7.3. Вычислить предел
![]() .
.
Решение.
Имеем неопределенность типа
![]() .
Вынося за скобки общий множитель
.
Вынося за скобки общий множитель
![]() ,
преобразуем рассматриваемое выражение,
используя свойства логарифмов:
,
преобразуем рассматриваемое выражение,
используя свойства логарифмов:
![]() .
.
Введем
обозначение
![]() .
В силу теоремы 4.1 (об обращении бесконечно
малых и бесконечно больших) если
.
В силу теоремы 4.1 (об обращении бесконечно
малых и бесконечно больших) если
![]() ,
то
,
то
![]() .
Используя теорему 7.2, получим:
.
Используя теорему 7.2, получим:
![]() .
.
