
Решение
![]() =
0,(020408163265306122448979591836734693877551).
Если
просуммировать геометрическую прогрессию
2/102
+ 4/104
+..., то получается в точности 1/49.
=
0,(020408163265306122448979591836734693877551).
Если
просуммировать геометрическую прогрессию
2/102
+ 4/104
+..., то получается в точности 1/49.
14. Пусть (n, 10) = 1, m < n, (m, n) = 1, и t — наименьшее число такое, что 10t - 1 делится на n. Докажите, что t кратно длине периода дроби m/n. Будет ли это длина периода? Сложность: 4- Классы: 8,9,10
Решение
Если 10t
![]() 1(mod
n),
то остатки r0
и rt
(см. задачу 5.41
) совпадают, так как r0
= m
и rt
1(mod
n),
то остатки r0
и rt
(см. задачу 5.41
) совпадают, так как r0
= m
и rt
![]() 10tm(mod
n).
Значит период дроби m/n
делит t.
Наоборот, если T —
длина периода, то rT
= r0
(дробь чисто периодическая согласно
задаче 5.41
) и r010T
10tm(mod
n).
Значит период дроби m/n
делит t.
Наоборот, если T —
длина периода, то rT
= r0
(дробь чисто периодическая согласно
задаче 5.41
) и r010T
![]() r0(mod
n).
Так как r0
= m
и (m,
n) =
1, то полученное сравнение можно сократить
на r0.
Следовательно, 10T
r0(mod
n).
Так как r0
= m
и (m,
n) =
1, то полученное сравнение можно сократить
на r0.
Следовательно, 10T
![]() 1(mod
n).
1(mod
n).
15.
Обозначим через L(m)
длину периода дроби 1/m.
Докажите, что если (m,
10) = 1, то L(m)
является делителем числа
![]() (m).
Сложность: 4
Классы: 9,10,11
(m).
Сложность: 4
Классы: 9,10,11
16.
Эффект девяток.
Периодом дроби 1/7 является число N
= 142 857. Оно обладает следующим свойством:
сумма двух половин периода — число из
одних девяток ( 142 + 857 = 999). Докажите в
общем случае, что для простого q
> 5 и натурального p
< q
период дроби p/q
есть 2n-значное
число N
=
![]() такое,
что N1
+ N2
=
такое,
что N1
+ N2
=
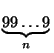 .
Сложность: 4+
Классы: 8,9,10,11
.
Сложность: 4+
Классы: 8,9,10,11
Решение
Пусть t
= 2n —
длина периода. Согласно задаче 5.43
, выполняется сравнение 10t
![]() 1(mod
q).
Отсюда 10n
1(mod
q).
Отсюда 10n
![]() -
1(mod q)
и
-
1(mod q)
и
![]() +
+
![]()
![]()
![]() =
1. Но в десятичной системе эти дроби
имеют вид
=
1. Но в десятичной системе эти дроби
имеют вид
![]() =
0,
=
0,![]() ,
, ![]() = 0,
= 0,![]() ,
,
поэтому N1
+ N2
=
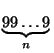 .
.
17.
Пусть (m,
n) =
1. Докажите, что сумма длин периода и
предпериода десятичного представления
дроби m/n
не превосходит
![]() (n).
Сложность: 4+
Классы: 10,11
(n).
Сложность: 4+
Классы: 10,11
18. Обозначим через L(m) длину периода дроби 1/m. Докажите, что если (m1, 10) = 1 и (m2, 10) = 1, то справедливо равенство L(m1m2) = [L(m1), L(m2)]. Чему равна длина периода дроби 1/m1 + 1/m2? Сложность: 4+ Классы: 10,11
19. Пусть число m имеет вид m = 2a5bm1, где (10, m1) = 1. Положим k = max(a, b). Докажите, что период дроби 1/m начинается с (k + 1)-ой позиции после запятой, и имеет такую же длину, как и период дроби 1/m1. Сложность: 4+ Классы: 9,10,11
20. Загадочное число. Число N = 142 857 обладает и рядом других свойств. Например: 2 . 142 857 = 285 714, 3 . 142 857 = 428 571..., то есть при умножении на 1, 2, 3,..., 6 цифры циклически переставляются; 14 + 28 + 57 = 99; N2 = 20 408 122 449, 20 408 + 122 449 = 142 857 = N. Аналогичные операции можно проделывать и с другими периодами дробей. Что получается для чисел 1/17, 1/19? Объясните эти факты. Сложность: 4+ Классы: 8,9,10,11
Решение
При разложении 1/7 в десятичную дробь последовательность остатков устроена следующим образом:
r0 = 1, r1 = 3, r2 = 2, r3 = 6, r4 = 4, r5 = 5, r6 = 1,...
Первое свойство объясняется равенствами
2 .
![]() =
=
![]() , 3
.
, 3
.
![]() =
=
![]() , 4
.
, 4
.
![]() =
=
![]() ,...
,...
Объяснение второго
свойства получается, если в равенстве
![]() +
+
![]() +
+
![]() =
1 перейти к десятичной записи.
Чтобы
объяснить последнее свойство, запишем
N в
виде N
= (106
- 1)/7. Отсюда N2
= (106
- 1)2/49.
Число, которое получается сложением
половинок числа N2,
будет периодом дроби
=
1 перейти к десятичной записи.
Чтобы
объяснить последнее свойство, запишем
N в
виде N
= (106
- 1)/7. Отсюда N2
= (106
- 1)2/49.
Число, которое получается сложением
половинок числа N2,
будет периодом дроби
![]()
![]() =
N2
=
N2![]() =
=
 =
=
![]() .
.
Так как
![]()
![]()
![]() =
=
![]() =
0,(142857),
=
0,(142857),
то из половинок числа N2 получится число N.
21. Найдите последние три цифры периодов дробей 1/107, 1/131, 1/151. (Это можно сделать, не считая предыдущих цифр.) Сложность: 4+ Классы: 10,11
22. Число Фейнмана. Объясните поведение следующей десятичной дроби и найдите ее период:
![]() =
0, 004 115 226 337 448...
=
0, 004 115 226 337 448...
Сложность: 5 Классы: 9,10,11
Ответ
![]() =
0,(004 115 226 337 448 559 670 781 893).
=
0,(004 115 226 337 448 559 670 781 893).
23.
Коля Васин задумал написать программу,
которая дала бы возможность компьютеру
печатать одну за другой цифры десятичной
записи числа
![]() .
Докажите, что даже если бы машина не
ломалась, то Колина затея все равно бы
не удалась, и рано или поздно компьютер
напечатал бы неверную цифру. Сложность:
4
Классы: 8,9,10,11
.
Докажите, что даже если бы машина не
ломалась, то Колина затея все равно бы
не удалась, и рано или поздно компьютер
напечатал бы неверную цифру. Сложность:
4
Классы: 8,9,10,11
24. Автор: А. Карагулян
a1, a2, a3, ..., an, ... — возрастающая последовательность натуральных чисел. Известно, что an + 1 ≤ 10an при всех натуральных n. Доказать, что бесконечная десятичная дробь 0, a1a2a3..., полученная приписыванием этих чисел друг к другу, непериодическая. Сложность: 3+ Классы: 8,9,10
