Література

1. Басакер Р., Саати Т. Конечные графы и сети. – М.: Наука, 1974. – С. 3-16, 136-143.

2. Белов В.В., Воробьев Е.М., Шаталов В.Е. Теория графов. – М.: Высшая школа, 1976. – С.7-14.

3. Дискретная математика для програмистов / Ф.А.Новиков. – СПб.: Питер, 2002. – С.189-198.

4. Капітонова Ю.В., Кривий С.Л., Летичевський О.А., Луцький Г.М., Печорін М.К. Основи дискретної математики. – К.: Наукова думка, 2002. – С.224-229, 236-243.

5. Свами М., Тхуласираман К. Графы, сети и алгоритмы. – М.: Мир, 1984. – С.11-23, 78-84.

Тема 2.2. Операції над графами

2.2.1. Поняття графа

Існують різні перетворення заданих графів, в результаті яких отримують нові графи. Ці перетворення називають операціями над графами.

2.2.1.1. Операція вилучення ребра (дуги). Якщо G(X,Г) – заданий граф і – його ребро (дуга), то граф G₁(X,Г\{и}) називають графом, отриманим з G вилученням ребра (дуги). Кінцеві вершини вилученого ребра (дуги) із множини Х не вилучаються.

2.2.1.2. Операція вилучення вершини. Якщо G(X,Г) – заданий граф і – його вершина, то граф G₂(X\{х},Г) називають графом, отриманим з G вилученням вершини, якщо із множини Г вилучено всі ребра (дуги), інцидентні вилученій вершині.

2.2.1.3. Операція введення ребра (дуги). Якщо G(X,Г) – заданий граф, – його вершини, причому , то граф G₃(X,Г{(х₁,х₂)}) називають графом, отриманим з G введенням ребра (дуги).

2.2.1.4. Операція введення вершини. Якщо G(X,Г) – заданий граф, – його ребро (дуга) і , то граф G₄(X{х},Г) називають графом, отриманим з G введенням вершини, якщо із множини Г вилучено ребро (дугу) і введено два нових – .

2.2.1.5. Операція об’єднання графів. Якщо G(X,Г) і G*(X*,Г*) – задані графи, то граф G₅(XX*,ГГ*) називають об’єднанням графів G та G*.

2.2.1.6. Операція перерізу (перетину) графів. Якщо G(X,Г) і G*(X*,Г*) – задані графи, то граф G₆(XX*,ГГ*) називають перерізом графів G та G*.

2.2.1.7. Операція віднімання графів. Якщо G(X,Г) і G*(X*,Г*) – задані графи, то граф G₇(X,Г\Г*) називають різницею графів G та G*.

2.2.1.8. Операція строгої диз’юнкції графів. Якщо G(X,Г) і G*(X*,Г*) – задані графи, то реберно породжений граф G₈: [ГГ*] називають симетричною різницею графів G та G*.

2.2.1.9. Операція множення графів. Якщо G(X,Г) і G*(X*,Г*) – задані графи, то граф G₈(XХ*,Г**) називають добутком графів G та G*, якщо тоді і тільки тоді, коли .

Для операції над матрицями при визначенні об’єднання, перетину, різниці, симетричної різниці використовують правила:

00=0 00=0 0\0=0 00=0

01=1 01=0 0\1=0 01=1

10=1 10=0 1\0=1 10=1

11=1 11=1 1\1=1 11=0

Щоб розглянути матрично добуток графів, впорядковують елементи ХХ* так:

,

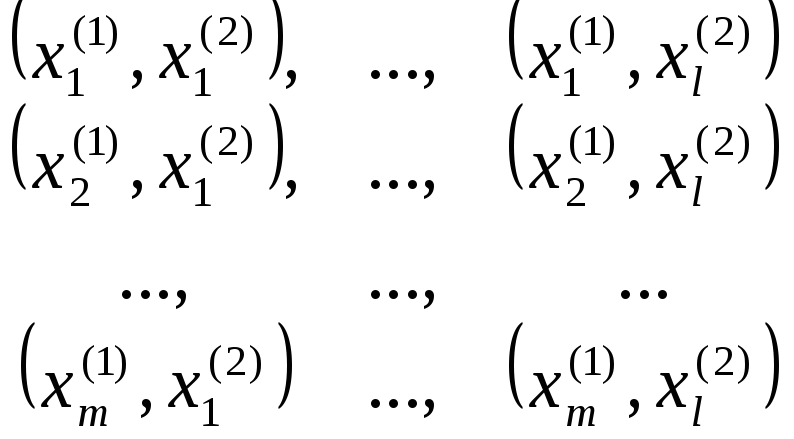де п і т – кількості вершин графів G та G*, тобто .

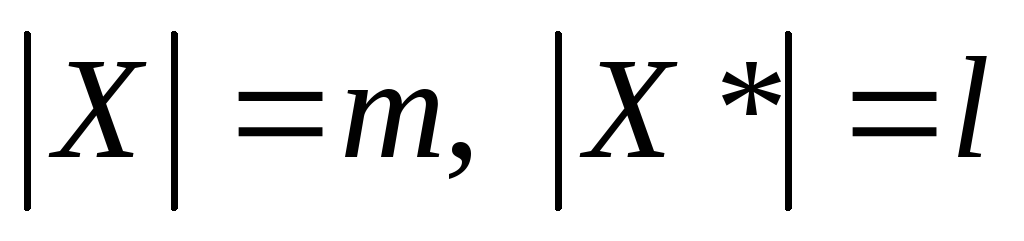Тоді якщо А=а_ij⁽¹⁾, А*=а_ij⁽²⁾ – матриці суміжностей вершин графів G та G* відповідно, то А**=b_(I,k),(j,l)= а_ij⁽¹⁾а_ij⁽²⁾ – матриця суміжності вершин графа G**=GG*:

.

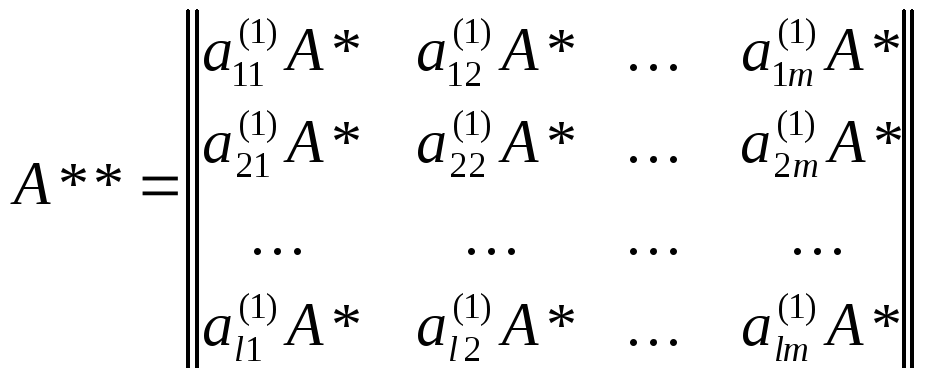Наприклад, нехай задано графи G та G* так:

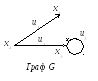
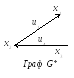
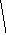
З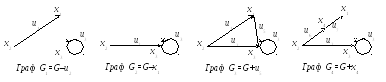дійснимо над цими графами всі описані вище операції.

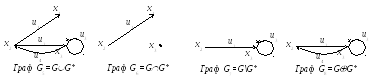
Для геометричного зображення графа добутку, не беручи до уваги орієнтацію графів G та G*, побудуємо спочатку його матрицю суміжності вершин за матрицями суміжності вершин графів G та G*.

.

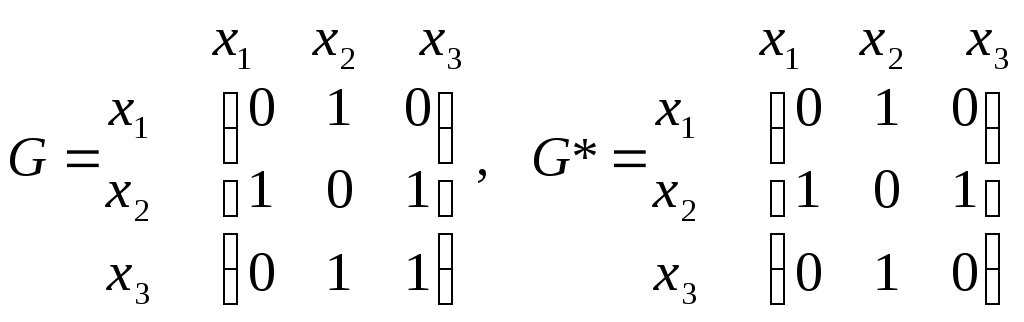
Кожну вершину графа зображуємо впорядкованою парою і з’єднуємо відповідні пари за матрицею суміжності вершин.