
- •1.1.1. Поняття множини
- •1.1.2. Елементи множини
- •1.1.3. Рівність множин
- •1.1.4. Задання та запис множин
- •1.1.5. Підмножини. Універсальна множина.
- •1.1.6. Операції над множинами та їхні властивості
- •Доведемо обернене включення:.
- •1.1.7. Потужність множин
- •Література
- •1.2.1. Поняття впорядкованої пари
- •1.2.2. Декартовий (прямий) добуток множин
- •1.2.3. Бінарні відношення
- •1.2.4. Переріз відношення. Фактор-множина
- •1.2.5. Способи задання відношень
- •Література
- •Тема 1.3. Властивості відношень
- •1.3.1. Теоретико-множинні операції над відношеннями
- •1.3.2. Композиція відношень
- •1.3.3. Обернені відношення
- •1.3.4. Рефлексивні, симетричні і транзитивні відношення
- •1.3.5. Відношення еквівалентності
- •1.3.6. Відношення порядку
- •1.3.7. Відображення і функції
- •Література
- •Розділ 2. Теорія графів Тема 2.1. Основні елементи теорії графів
- •2.1.1. Поняття графа
- •2.1.2. Ізоморфізм графів. Підграф. Суграф. Частковий граф
- •2.1.3. Числові характеристики графа
- •2.1.4. Маршрути незамкнені (ланцюги, шляхи) і замкнені (цикли, контури). Повнота. Зв’язність. Сильна зв’язність
- •2.1.5. Способи задання графа
- •Література
- •Тема 2.2. Операції над графами
- •2.2.1. Поняття графа
- •Тема 2.3. Дерева і цикли у графах
- •2.3.1. Компоненти зв’язності
- •Розглянемо незв’язний неорієнтований граф .
- •Отже, наведений на прикладі граф має три компоненти зв’язності.
- •2.3.2. Ранг та цикломатичне число графа
- •Якщо граф – вироджений, тобто має лише вершини, а ребра – відсутні, то і . За теоремою 2.3.2 додавання нового ребра збільшує або , або . Отже, числа та можуть лише зростати.
- •2.3.3. Дерева і ліси
- •Література
- •Тема 2.4. Розфарбування графа
- •2.4.1. Задача про чотири фарби. Правильне розфарбування графа
- •2.5.2. Визначення хроматичного числа. Хроматичний поліном
- •Розділ 3. Загальна алгебра Тема 3.1. Групи
- •3.1.1. Поняття алгебраїчної операції
- •3.1.2. Означення і приклади груп
- •Тема 3.2. Кільця
- •3.2.1. Поняття множини з подвійною композицією
- •3.2.2. Числові кільця
- •3.2.3. Абстрактні кільця
- •3.2.4. Гомоморфізми кілець
- •Тема 3.3. Поля
- •3.3.1. Означення поля. Приклади полів
- •3.3.2. Властивості полів
- •Розділ 4. Комбінаторний аналіз
- •Тема 4.1. Основні поняття комбінаторного аналізу
- •4.1.1. Основні правила комбінаторики
- •Розв’язання
- •4.1.2. Розміщення. Розміщення з повтореннями
- •Розв’язання
- •Розв’язання
- •4.1.3. Перестановки. Перестановки з повтореннями
- •Розв’язання
- •Розв’язання
- •4.1.4. Комбінації. Комбінації з повтореннями
- •Розв’язання
- •Розв’язання
- •Розв’язання
- •4.1.6. Біном Ньютона. Трикутник Паскаля. Властивості біноміальних коефіцієнтів
- •Розділ 5. Основи логіки Тема 5.1. Висловлення та операції над ними
- •5.1.1. Висловлення. Висловлювальна форма. Функція істинності
- •5.1.2. Операції над висловленнями
- •5.1.3. Таблиці істинності
- •5.1.4. Тавтології і суперечності.
- •5.1.5. Рівносильність формул. Властивості логічних операцій
- •Тема 5.4. Булеві функції
- •5.4.1. Поняття булевої функції. Способи задання
- •Тема 5.5. Логіка предикатів
- •5.5.1. Предикати, логічні операції над ними
- •5.4.2. Квантифікація предикатів. Квантор існування і квантор загальності
Розв’язання
![]() .
.
Означення
4.1.5. Нехай
![]() .
Перестановкою з
повтореннями з п
елементів називають будь-яке впорядковання
п-множини,
серед елементів якої є однакові. Якщо
серед елементів множини М
є
.
Перестановкою з
повтореннями з п
елементів називають будь-яке впорядковання
п-множини,
серед елементів якої є однакові. Якщо
серед елементів множини М
є
![]() елементів першого типу,
елементів першого типу,
![]() елементів другого типу,
елементів другого типу,
...
![]() елементів k-го
типу
елементів k-го
типу
![]() ,
,
то
кількість всіх перестановок такої
множини з повтореннями позначують
![]() .
.
Теорема 4.1.5. Має місце формула:
![]() .
.
Приклад. Скільки перестановок можна зробити з літер слова “Міссісіпі”?
Розв’язання
Оскільки літера “м” входить до слова 1 раз, літера “і” – 4 рази, “с” – 3 рази, “п” – 1 раз, а всіх літер у слові 9, то
![]()
4.1.4. Комбінації. Комбінації з повтореннями
У тих випадках, коли нас не цікавить порядок елементів у розміщення, а лише його склад, вводять поняття комбінації..
Означення
4.1.6. Нехай
![]() ,
тобто множина
,
тобто множина
![]() складається
з
складається
з
![]() елементів,
елементів,
![]()
![]() .
Комбінацією без
повторень з
.
Комбінацією без
повторень з
![]() елементів по
елементів по
![]() називають довільну k-
підмножину
називають довільну k-
підмножину
![]() множини
множини
![]()
![]() ,
всі елементи якої різні.
,
всі елементи якої різні.
Кількість різних комбінацій
з
![]() елементів по
елементів по
![]() без повторень позначають:
без повторень позначають:
![]() .
.
Отже, комбінація не є впорядкованою множиною, на відміну від розміщення, тобто дві різні комбінації відрізняються хоча б одним елементом.
Теорема 4.1.6.
Для довільних натуральних чисел
![]() і
і
![]()
![]() має місце формула:
має місце формула:
![]() .
.
Теорема 4.1.7.
Для
![]() виконується рівність:
виконується рівність:
![]() .
.
Доведення
Серед розміщень з
![]() елементів по
елементів по
![]() можна виділити класи впорядкованих
k-множин,
які відрізняються лише порядком
розміщення одних і тих самих елементів.
У кожному класі таких множин буде
можна виділити класи впорядкованих
k-множин,
які відрізняються лише порядком
розміщення одних і тих самих елементів.
У кожному класі таких множин буде
![]() ,
а кількість різних класів –
,
а кількість різних класів –
![]() .
Отже,
.
Отже,
![]() .
.
Приклад. Скільки діагоналей у правильному п-кутнику?
Розв’язання
Кількість пар вершин в п-кутнику, серед яких одні визначають діагональ, а інші – сторону п-кутника дорівнює:
![]() .
.
Оскільки всіх сторін п, кількість діагоналей визначатимемо так:
![]() .
.
Приклад. Скільки натуральних дільників має число 2310=235711?
Розв’язання
Кожен дільник, який не дорівнює
одиниці, має вигляд:
![]() ,
де
,
де
![]() .
.
Оскільки порядок множників
у добутку – неістотний, то кожен дільник
задається комбінацією з 5 по k,
де
![]() .
Всього дільників буде:
.
Всього дільників буде:
![]() .
.
Означення
4.1.7. Комбінацією
з повтореннями з п
елементів по k називають
довідний k-елементний
набір виду
![]() ,
де кожен з елементів
,
де кожен з елементів![]() належить до одного з п
типів.
належить до одного з п
типів.
Кількість різних комбінацій
з повтореннями позначують
![]() .
.
Теорема 4.1.8.
Кількість різних комбінацій з повтореннями
з
![]() елементів по
елементів по
![]() ,
де
,
де
![]() і
і
![]() – довільні натуральні числа дорівнює:
– довільні натуральні числа дорівнює:
![]() .
.
Приклад. У кондитерський відділ завезли 4 види тістечок. Скількома способами можна купити 7 тістечок?
Розв’язання
![]() .
.
4.1.6. Біном Ньютона. Трикутник Паскаля. Властивості біноміальних коефіцієнтів
З елементарної математики відомі формули скороченого множення:
![]() .
.
Ці формули можна записати і так:
![]() .
.
Очевидно, існує загальна закономірність.
Теорема 4.1.9. Справедлива рівність:
![]() .
.
Цю рівність називають біномом Ньютона.
Біноміальні коефіцієнти можна подати у вигляді трикутної таблиці, яку називають трикутником Паскаля:
-
1
1
п=1
1
2
1
п=2
1
3
3
1
п=3
1
4
6
4
1
п=4
1
5
10
10
5
1
п=5
...
У п-му рядку трикутника Паскаля кожен коефіцієнт розкладу, крім двох крайніх, що дорівнюють 1, – це сума відповідних коефіцієнтів із попереднього рядка.
Узагальненням бінома Ньютона є наступна теорема:
Теорема 4.1.10 (поліноміальна теорема). Справедлива рівність:
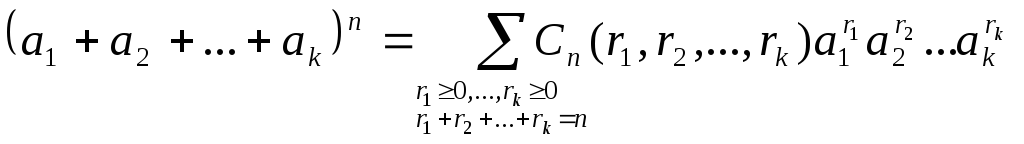 ,
,
де
![]() .
.
Числа
![]() називають біноміальними
коефіцієнтами.
називають біноміальними
коефіцієнтами.
Властивості біноміальних коефіцієнтів:
-
 (випливає з теореми 4.1.6, якщо
замінити у формулі k
на (n–k),
то (n–k)
заміниться на (n–
(n–k))=k).
(випливає з теореми 4.1.6, якщо
замінити у формулі k
на (n–k),
то (n–k)
заміниться на (n–
(n–k))=k). -
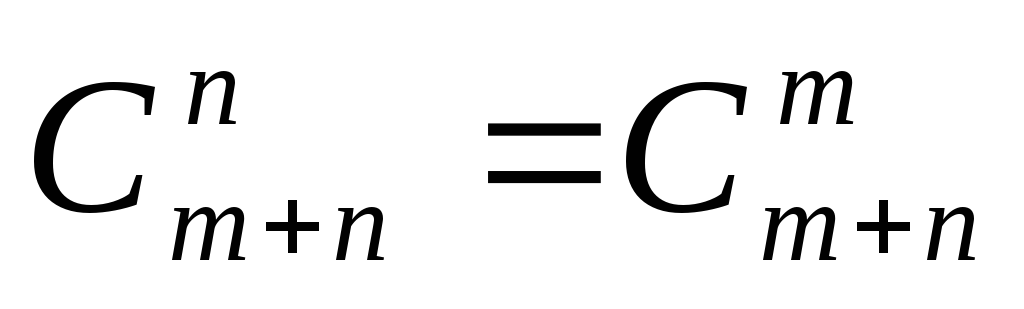 (формула симетрії).
(формула симетрії). -
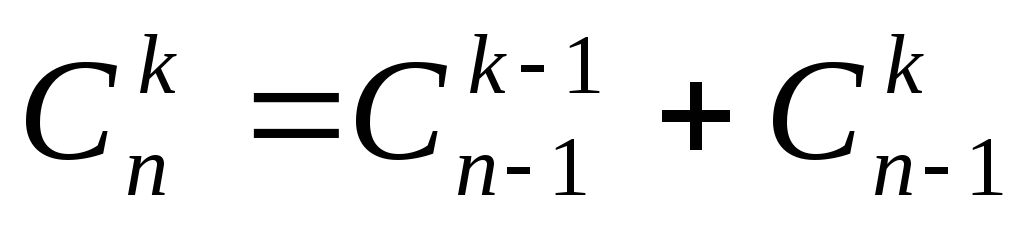 (формула додавання).
(формула додавання). -
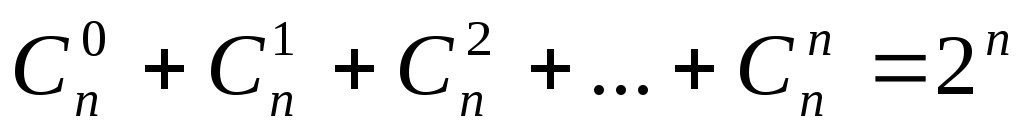 (
(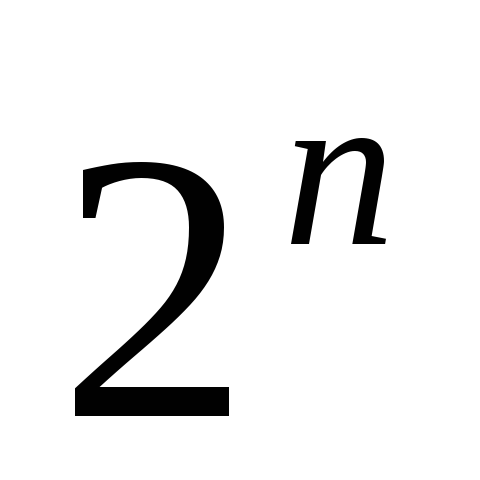 – кількість всіх розміщень з повтореннями
з елементів 2-х типів).
– кількість всіх розміщень з повтореннями
з елементів 2-х типів). -
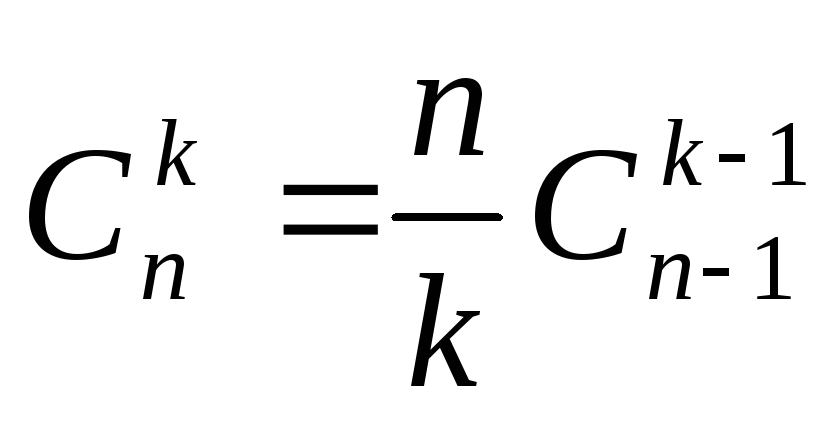 (формула винесення за дужки).
(формула винесення за дужки). -
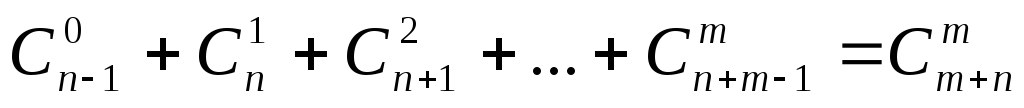 .
. -
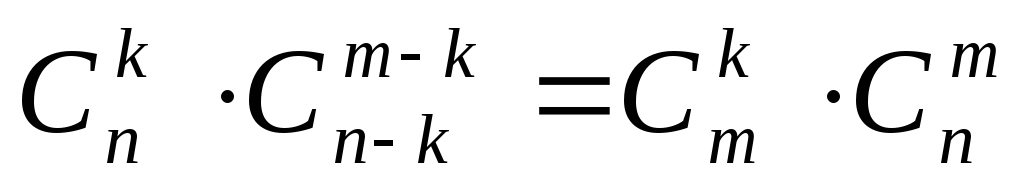 .
.
