2. Определители 2-ого и 3-ого порядка

Пусть дана квадратная таблица из четырех чисел

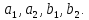
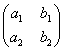(1).

Число называется определителем второго порядка, соответствующего таблице (1). Этот определитель обозначается символом ; соотвественно имеем 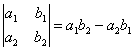(2).

Числа 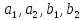называются элементами определителя. Говорят, что элементы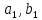 , лежат на главной диагонали определителя, 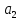, 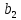- на побочной. Таким образом, определитель второго порядка равен разности между произведениями элементов, лежащих на главной и побочной диагоналях. Например,.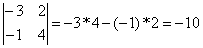

Для введения понятия – определитель третьего порядка рассмотрим систему трёх линейных уравнений с тремя неизвестными:

a₁₁x₁+ a₁₂x₂+ a₁₃x₃=b₁

a₂₁x₁+ a₂₂x₂+ a₂₃x₃=b₂ (1)

a₃₁x₁+ a₃₂x₂+ a₃₃x₃=b₃

Чтобы найти х₁ умножим уравнения системы (1) соответственно на а₂₂а₃₃ - а₃₂а₂₃, а₃₂а₁₃-а₁₂а₃₃, а₁₂а₂₃-а₂₂а₁₃ и сложим получаемые левые и правые части. После приведения подобных членов (относительно х₁, х₂ и х₃) окажется, что коэффициенты при х₂ и х₃ равны нулю. Предполагая, что коэффициент при х₁ отличен от нуля, получим:

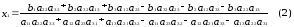
Составим таблицу чисел из коэффициентов при неизвестных х₁, х₂ и х₃ системы (1):

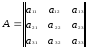
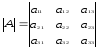
Эта таблица чисел называется квадратной матрицей 3-го порядка (у неё три строки и три столбца). Выражение, стоящее в знаменателе формулы (2), можно составить из чисел матрицы А по следующему правилу. Произведение чисел, расположенных на главной диагонали, и два произведения чисел, расположенных в вершинах двух равнобедренных треугольников с основанием, параллельным главной диагонали, и с вершиной в противоположном углу, берутся со знаком плюс. Три произведения, которые строятся по такому же правилу, но относительно второй диагонали, берутся со знаком минус.

Составленная таким образом сумма шести слагаемых (из которых три взяты со знаком плюс, а три – со знаком минус) называется определителем 3-го порядка матрицы А и обозначается через:

3. Векторы, действия над ними

Вектором называется направленный отрезок. Если у отрезка AB его концы равноправны, то для вектора один из концов отрезка, например, A называется началом, а другой, то есть B, – концом. Обозначим вектор либо указанием концов отрезка, причем начало вектора ставится на первое место, либо строчной латинской буквой со стрелкой или чертой над буквами. Векторы и называются одинаково направленными или сонаправленными, если лучи AB и CD одинаково направлены. Если лучи AB и CD противоположно направлены, векторы и называются противоположно направленными. Два вектора называются коллинеарными, если они лежат на одной прямой или на параллельных прямых. Абсолютной величиной (или модулем) вектора называется длина отрезка, изображающего вектор. Абсолютную величину вектора обозначим Два вектора называются равными, если они одинаково направлены и равны по абсолютной величине.

Одна точка такого отрезка является началом, а другая граничная тока — концом вектор. Вектор обозначается или , где является началом вектора, а— концом. Длина вектора (также называемый его модулем) обозначается какили .

Нуль-вектором именуется вектор, в котором конец совпадает с его началом.

 

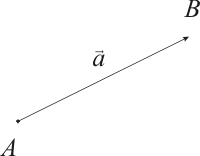Рис. 2.1

Вектор называется единичным, если его абсолютная величина равна единице.

О: Коллинеарными именуются векторы, которые расположены на параллельных (к примеру, на одной) прямых, а компланарными называются векторы, которые находятся в параллельных плоскостях.

О: Равными являются векторы, которые: 1) коллинеарны; 2) направлены одинаково ( то есть сонаправлены — ↑↑); 3) обладают равными модулями.

Таким образом, существует возможность переноса вектора параллельно самому себе, при перемещении началав любую прочую точку. Векторы подобного типа именуются свободными.

Линейные операции, выполняемые над векторами: сложение, вычитание и умножение на число.

Сложение векторов

Суммойисовмещён с началом векторас концом вектора(рис. 2.2, а).

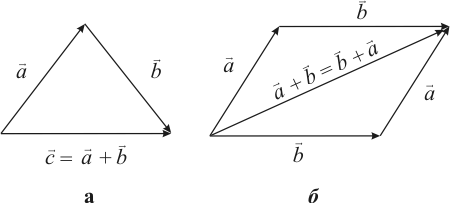
Рис. 2.2

 

Свойства сложения векторов:

1⁰. Переместительный закон (коммутативность):

Доказательство выводится из рисунка 2.2, б. На этом же рисунке показано правило параллелограмма при сложении векторовибудет вектор, который совпадает с диагональю параллелограмма, берущей начало из общего начала векторов.

2⁰. Сочетательный закон:

Доказательство выводится из рис. 2.3. На этом же рисунке дано правило сложения нескольких векторов, в случае когда начало следующего вектора совмещается с концом предыдущего. Сумма представляет собой вектор, который соединяет начало первого вектора с концом последнего слагаемого вектора.

 

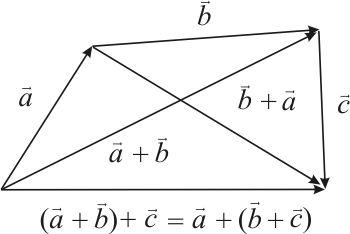
Рис. 2.3

Вычитание векторов

Разностьюивекторовиявляется вектор, для которого справедливо. Исходя из определения имеем правило построения вектора, когда начала обоих векторовсовмещены: необходимо совместить конец вычитаемого векторас концом уменьшаемого вектора(рис 2.4).

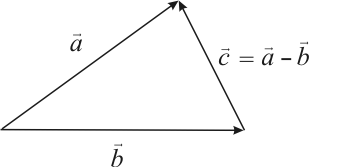
Рис. 2.4

 

Умножение вектора на число

Произведением векторана число и направлен в ту же сторону если() и противоположную сторону если() .

Свойства умножения вектора на число:

1⁰. Сочетательное свойство (ассоциативность):

.

2⁰. Распределительное свойство (дистрибутивность):

Свойства легко проверяются геометрически.