
- •Пермь 2007
- •Рекомендованная литература
- •Контрольные вопросы
- •Параллельный перенос осей координат.
- •Поворот осей координат.
- •Образец задания
- •Пусть уравнение кривой второго порядка имеет вид
- •Рассмотрим уравнение кривой второго порядка общего вида
- •Дано уравнение кривой
- •Варианты заданий
- •Вариант № 1
- •5. Составить уравнение линии, каждая точка которой одинаково удалена от начала координат и точки .
- •Вариант № 8
-
Параллельный перенос осей координат.
Даны
две системы координат с разными началами
![]() и
и
![]() и одинаковыми направлениями осей
(рис.1). Обозначим через
и одинаковыми направлениями осей
(рис.1). Обозначим через
![]() и
и
![]() координаты произвольной точки
координаты произвольной точки
![]() соответственно в старой
соответственно в старой
![]() и новой
и новой
![]() системах координат. Если
системах координат. Если
![]() координаты нового начала
координаты нового начала
![]() в системе
в системе
![]() ,
то справедливы формулы преобразования
параллельного переноса осей координат
,
то справедливы формулы преобразования
параллельного переноса осей координат
![]() ,
,
![]() , или (2)
, или (2)
![]() ,
,
![]() .
.

Рис. 1 Рис. 2
-
Поворот осей координат.
Даны
две системы координат с одинаковым
началом и разными направлениями осей.
Пусть
![]() (рис.2) – угол между
(рис.2) – угол между
![]() и
и
![]() (угол поворота системы координат).
Справедливы формулы преобразования
поворота осей координат
(угол поворота системы координат).
Справедливы формулы преобразования
поворота осей координат
![]() (3)
(3)
![]() ,
,
где
![]() координаты произвольной точки в
координаты произвольной точки в
![]() ,
,
![]() координаты этой точки в новой системе
координат
координаты этой точки в новой системе
координат
![]() .
.
Образец задания
-
Дано уравнение гиперболы в виде
 . Путем параллельного переноса системы
координат привести ее уравнение к виду
. Путем параллельного переноса системы
координат привести ее уравнение к виду
 ,
указать асимптоты гиперболы, построить
соответствующие системы координат и
данную гиперболу по уравнению
,
указать асимптоты гиперболы, построить
соответствующие системы координат и
данную гиперболу по уравнению
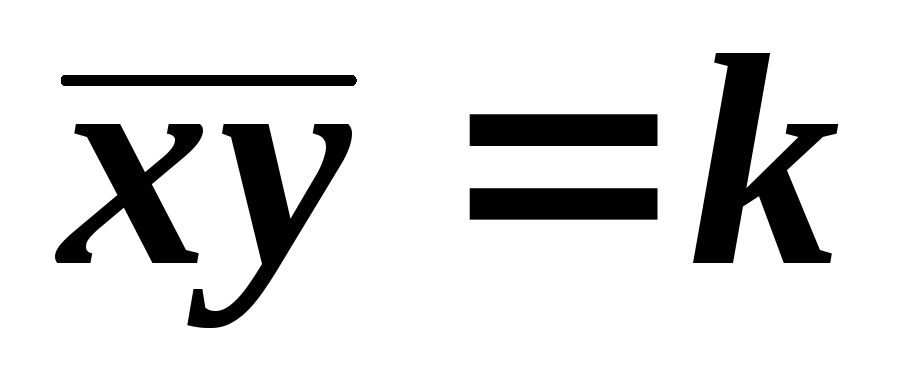 .
. -
Даны уравнения кривых второго порядка :
а)
![]() ,
,
б)
![]() .
.
Требуется по данному уравнению определить, какого типа кривую (эллиптического, гиперболического, параболического) оно представляет, затем следует привести это уравнение к каноническому виду с помощью параллельного переноса системы координат, построить соответствующие системы координат и кривую по ее каноническому уравнению.
-
Дано уравнение кривой второго порядка
![]() .
.
Требуется привести данное уравнение путем поворота и параллельного переноса системы координат к каноническому виду. Построить соответствующие системы координат и данную кривую по ее каноническому уравнению.
-
а) Дано уравнение кривой в полярных координатах
![]() .
.
Требуется построить эту кривую по ее полярному уравнению.
б) Дано уравнение кривой в прямоугольных декартовых координатах
![]() .
.
Записать это уравнение в полярных координатах, а затем построить данную линию по ее полярному уравнению.
-
Составить уравнение линии, каждая точка которой в два раза ближе к точке
 ,
чем к началу координат.
,
чем к началу координат.
Решение задания 1.
Из
школьного курса алгебры известно, что
график функции
![]() есть гипербола, асимптоты которой
параллельны
есть гипербола, асимптоты которой
параллельны
![]() и
и
![]() (см. Привалов, гл.5, §5, п.2). С другой стороны,
график функции
(см. Привалов, гл.5, §5, п.2). С другой стороны,
график функции
![]()
![]() гипербола, асимптоты которой есть
гипербола, асимптоты которой есть
![]() и
и
![]() .
Таким образом, взяв за координатные оси
асимптоты функции
.
Таким образом, взяв за координатные оси
асимптоты функции
![]() , мы приведем эту функцию к более простому
виду
, мы приведем эту функцию к более простому
виду
![]() (при этом пользуемся формулами
преобразования параллельного переноса
(2) ). Итак, в системе
(при этом пользуемся формулами
преобразования параллельного переноса
(2) ). Итак, в системе
![]() задана линия уравнением
задана линия уравнением
![]() .(4)
.(4)
Выполним
параллельный перенос системы
![]() по формулам (2)
по формулам (2)
![]() ,
,
![]() ,(2)
,(2)
где
![]() координаты нового начала
координаты нового начала
![]() в системе
в системе
![]() ;
;
![]() координаты произвольной точки в системе
координаты произвольной точки в системе
![]() ;
;
![]() координаты той же точки в системе
координаты той же точки в системе
![]() .
.
Воспользовавшись формулами (2), запишем уравнение (4) в виде
![]() .
.
Умножим
обе части этого уравнения на выражение
![]() и раскроем скобки, получим
и раскроем скобки, получим
![]() .
.
Сгруппируем
члены, содержащие
![]() ,
,
![]() .(5)
.(5)
Выберем
точку
![]() так, чтобы члены, содержащие
так, чтобы члены, содержащие
![]() , обратились в нуль, т.е. положим
, обратились в нуль, т.е. положим
![]() , откуда
, откуда
![]() координаты нового начала. Подставим
эти значения в уравнение (5), имеем
координаты нового начала. Подставим
эти значения в уравнение (5), имеем
![]() , или
, или
![]() .
(6)
.
(6)
Уравнение (6) – уравнение равнобочной гиперболы, асимптотами которой являются новые оси координат.
Изобразим
обе системы координат и построим данную
линию по ее уравнению (6) в системе
координат
![]() (рис.3)
(рис.3)

Рис. 3
Решение задания 2 (см. Привалов, гл.5, §6, п.3)
