Уральский технический институт связи и информатики (филиал)

Сибирского государственного университета

телекоммуникаций и информатики

(УрТИСИ ГОУ ВПО «СибГУТИ»)

КУРСОВАЯ РАБОТА

ПО ДИСЦИПЛИНЕ: Вычислительная математика

ФАМИЛИЯ: Кропин

ИМЯ: Артем

ОТЧЕСТВО: Григорьевич

ШИФР: Е001П007

ГРУППА: П-01с

Курсовая работа поступила в УрТИСИ ГОУ ВПО «СибГУТИ»

«_______» _______________________2011г.

Методист

Дата рецензии «_______» ______________________2011г.

Оценка ___________________________________________________

Подпись рецензента ________________________________________

Уральский технический институт связи и информатики (филиал)

Сибирского государственного университета

телекоммуникаций и информатики

(УрТИСИ ГОУ ВПО «СибГУТИ»)

КУРСОВАЯ РАБОТА

по дисциплине: Вычислительная математика

на тему: Освоение и применение методов вычислительной математики и способов визуализации данных при решении учебных и профессиональных задач.

Вариант 7

Выполнил:

студент группы П-01с

Кропин А.Г.

Екатеринбург, 2011

Постановка задачи

Рассматривается функция F(t,), представляющая собой финитную функцию, определенную на конечном носителе длины  и продолженную периодически (период T > ) на всю ось. С помощью языка программирования, визуальной среды программирования и методов гармонического анализа вычислить коэффициенты Фурье аппроксимирующего тригонометрического полинома на дискретном множестве точек периода, построить графики исходного сигнала, тригонометрического полинома для различных степеней, а также график спектра амплитуд сигнала. Выполнить решение задачи средствами математических пакетов в аналитическом виде. Сравнить спектры амплитуд дискретного и аналогового сигналов.

Полином:

Сигнал:

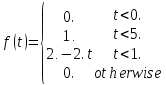
сигнал задан на отрезке [0..] функцией f(t) =1.

Вне этого отрезка f(t) равна нулю.

Рисунок сигнала:

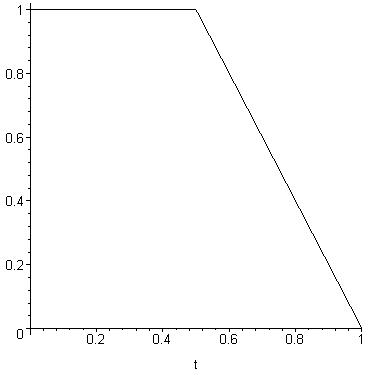
Содержание

1. Алгоритмы решения вспомогательных задач 5

1.1 Нахождение корня уравнения 5

1.2 Вычисление коэффициентов Фурье 7

1.3 Вычисление тригонометрического полинома и построение графиков функции. 8

1.4 Построение графика спектра амплитуд сигнала 9

2. Общий листинг программы в Delphi 10

3. Результаты расчетов 17

3.1 Расчет корня полинома 17

3.2 Расчет коэффициентов Фурье 17

Приложение №1. Блок-схемы 18

Блок-схема №1 (функция Max_derive) 18

Блок-схема №2 (процедура Iter) 19

Блок-схема №3 (процедура Trig) 20

Блок-схема №4 (процедура Button3Click) 22

Блок-схема №5 (процедура Button4.click) 24

Приложение №2. Графическая часть работы 25

Список литературы 28

1. Алгоритмы решения вспомогательных задач

1.1 Нахождение корня уравнения

Для определения периода Т необходимо вычислить корень заданного полинома. Вычислим его наименьший положительный корень методом простой итерации, определив первоначально интервал его расположения. Для этого вычислим знак полинома в точке x=0 и прибавляя заданный шаг, будем последовательно вычислять значения полинома в точках x=h, x=2h,… до точки, в которой знак полинома в нуле и в текущей точке (на правом конце интервала локализации корня) различные. Шаг как число вещественного типа зададим в режиме диалога в окне InputBox. Правый конец интервала расположения корня вычисляет функция Interval. Учитывая, что в процессе локализации корня значения полинома на правом конце интервала (переменная x в теле процедуры-функции Interval ) и в предыдущей точке (x-h) различаются по знаку, поэтому в качестве отрезка нахождения корня можно взять интервал [x-h, x].

Чтобы применить метод простой итерации в задаче нахождения корня уравнения f(x) = 0, необходимо уравнение представить в виде итерационного равенства 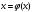. При этом, для сходимости итерационного процесса требуется выполнение условия 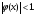Это требование можно выполнить, представив исходное уравнение в виде равенства 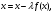подобрав множитель 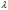так, чтобы выполнялись условия:

1. первая производная функции f(x) не меняет знак на интервале нахождения корня,

2. ,

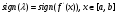3. абсолютная величина множителя 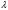находится в интервале [0, Q), где

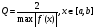
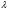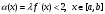При выполнении этих условий на величину функция в правой части итерационного равенства имеет производную , где и , следовательно условие сходимости выполнено и метод простой итерации сходится.

Для реализации метода итераций построим процедуру Iter , для работы которой необходимо построить дополнительные процедуры вычисления максимума производной полинома. Результаты этих вычислений выводятся на метки Label3 и Label4. Промежуточные вычисления шагов метода итераций выводим на компонент ListBox, обращение к свойствам и методам которого следует выполнять с указанием префикса Form1.

Функция Max_derive (блок-схема №1)

A,b – входные переменные вещественного типа – интервал поиска корня полинома, функция возвращает значение вещественного типа – max значение первой производной полинома на [a,b].

Derive – функция находящее значение первой производной полинома в заданной точке.

h – локальная константа, шаг изменения локальной переменной х

p – max значение производной на [a,b]

В функции вычисляется значение производной полинома на левом значении интервала, затем увеличивая x на h до тех пор пока не достигнем правого значения интервала, рассчитываем для каждого x значение производной полинома, сравнивая с предыдущим значением находим мах значение производной p на отрезке.

Процедура Iter (блок-схема №2)

Входные переменные a,b – интервал поиска корня.

Выходные переменные root, kiter – корень полинома и количество итераций соответственно.

Max_derive(a,b) – вызов функции определения мах производной на [a,b]

_Lambda – коэффициент

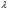
_{В цикле последовательно ищем корень заданного полинома по формуле 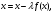до тех пор пока разность текущего и предыдущего значений x не более заданной точности eps.}

_{Найденный корень присваивается локальной переменной root.}

_{Вызов процедуры произведем в процедуре BitBtn1Click}

Iter(La,Rb,T,Kiter), где La, Lb – интервал поиска корня, Т – значение корня, Kiter – количество итераций.