III. Производная и ее приложения

Основные правила и формулы дифференцирования:

1. y = c, где c=const, .

2. y = x, y'=1.

3. .

4. .

5. .

6. .

7. .

8. .

9. .

10. .

11. .

12. .

13. .

14. .

15. .

16. .

17. .

18. .

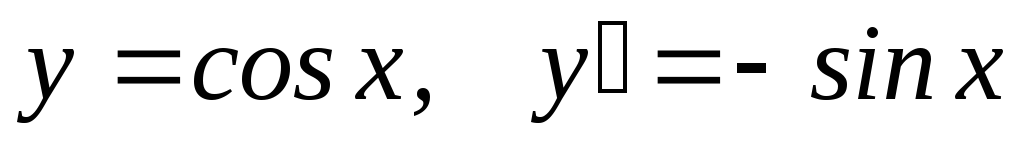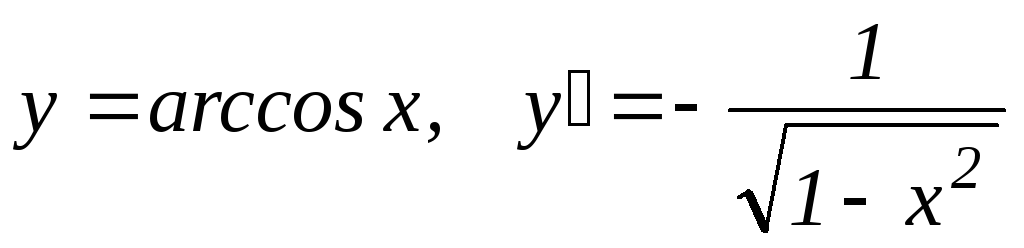19. - это правило дифференцирования сложной функции.

Пример 1. Найти производные данных функций

а) ; б) ;

в) ; г) <1;

д) ; е) .

Решение:

а) Применяя правило дифференцирования дроби и формулы (3); (16), имеем

б) Последовательно применяя правило дифференцирования сложной функции, правила и формулы дифференцирования, имеем:

в)

г)

д) Предварительно прологарифмируем по основанию е обе части равенства:

или .

Теперь дифференцируем обе части, считая lny сложной функцией от переменной x.

откуда

.

е) В данном случае зависимость между аргументом х и функцией у задана уравнением, которое не разрешено относительно функции у. Чтобы найти производную y', надо продифференцировать по х обе части заданного уравнения, считая при этом у функцией от х , а затем полученное уравнение решить относительно искомой производной y'. Имеем:

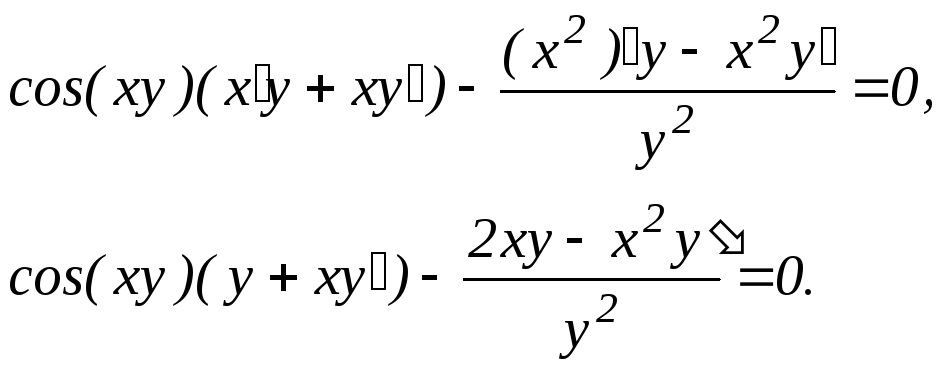
Из полученного равенства, связывающего х, у и y', находим производную y':

откуда

Пример 2. Найти производную второго порядка :

а)

б)

в)

Решение: а) Функция у задана в неявном виде. Дифференцируем по х обе части заданного уравнения, считая при этом у функцией от х:

откуда (1)

Снова дифференцируем по х обе части равенства (1):

(2)

Заменив y' в (2) правой частью (1), получим

.

б) Найдем первую производную данной функции

.

Найдем производную от первой производной, получим вторую производную функции :

в) Зависимость между переменными х и у задана параметрическими уравнениями. Чтобы найти производную y', находим сначала дифференциалы dy и dx и затем берем отношение этих дифференциалов:

Тогда

Производная второго порядка . Значит, чтобы найти y'',надо найти дифференциал dy':

Тогда

Формула Тейлора

(1)

С ее помощью можно вычислить приближенные значения функции f(x), если известны значения этой функции и ее производных до порядка n в «начальной» точке x=a и если, кроме того, удается оценить остаточный член R_n. Если

, то (2)

(3)

с погрешностью α₀.

Для оценки погрешности формулы (3) чаще всего используется запись остаточного члена R_n в форме Лагранжа:

И

, где ξ лежит между точками а и х. (4)

Пример 3. Применяя формулу Тейлора с остаточным членом в формуле Лагранжа, вычислить е^0,1 и е^0,2 с точностью 0,001.

Решение: Формула Тейлора с остаточным членом в форме Лагранжа для функции f(x)=e^x имеет вид:

где

Отсюда получим:

Значения х₁ = 0,1 и х₂ = 0,2 принадлежат отрезку [0;½],следовательно, 0<θx<0,5 и е^θx<e^0.5<2;

Требуется определить n так, чтобы выполнялось неравенство R_n<0,001 и х = 0,1.

Положим х = 0,1 и вычислим несколько первых членов разложения, сравнивая их с заданной точностью α = 0,001:

u₀=1=1,0000>α,

Итак, для вычисления е^0,1 с α=0,001 достаточно взять первые 4 слагаемых.

е^0,1≈1+0,1+0,005+0,0002≈1,1052≈1,105.

Полагая х=0,2 аналогично можно найти, что достаточно 5 слагаемых и е^0,2≈1,221.

Пример 4. Найти наибольшее и наименьшее значения функции у=3х-х³ на отрезке [-2;3].

Решение: Найдем производную: у' = 3-3х²=3(1-х²). Приравняв у' к нулю, находим стационарные точки: 3(1-х²)=0, т.е. х₁=1 и х₂=-1.

Определяем значения функции в этих точках:

f(1)=2,

f(-1)=-2.

Вычисляем значения данной функции на границах промежутка:

f(-2)=2,

f(3)=-18.

Из полученных четырех значений выбираем наибольшее и наименьшее. Итак, наибольшее значение функции на отрезке [-2;3] f_наиб = 2, а наименьшее f_наим = -18.

Пример 5. Исследовать методами дифференциального исчисления функцию и, используя результаты исследования, построить ее график.

Решение: Исследование функции проведем по следующей схеме:

1. Найдем область определения функции.

2. Исследуем функцию на четность и нечетность.

3. Найдем точки пересечения графика функции с осями координат.

4. Исследуем функцию на непрерывность; найдем точки разрыва (если они

существуют) и установим характер разрыва.

5. Найдем асимптоты кривой у = f(x).

6. Найдем интервалы возрастания и убывания функции и ее экстремумы.

7. Найдем интервалы выпуклости и вогнутости кривой и точки ее перегиба.

Реализуем данную схему.

1. Функция определена при всех значениях аргумента х, кроме х=±2, т.е. область определения функции D(y) = (-∞;-2)U(-2;2)U(2;+∞).

2. Для установления четности или нечетности функции проверим выполнимость равенств для любых х и –х из области определения функции:

   1. Если f(-x) = f(x), тогда f(x) - функция четная, т. е. ее график симметричен относительно оси Оу;

   2. Если f(-x) = -f(x), тогда f(x) - функция нечетная, т. е. ее график симметричен относительно начала координат т. О(0;0).

Итак, , следовательно, данная функция является нечетной.

3. Для нахождения точек пересечения графика функции с осью Ох полагаем у=0; с осью Оу — х=0.

х=0; у=0.

у=0,

Т.е., график функции пересекает систему координат в т. О(0;0).

4. Данная функция является элементарной, поэтому она непрерывна на своей области определения D(у).Найдем односторонние пределы функции в указанных точках:

.

Т.о., в точках х=±2 функция имеет разрыв второго рода и прямых х = -2 и х = 2 – вертикальные асимптоты графика функции.

5. Найдем наклонные асимптоты у=kx+b, где

Т.о., наклонная асимптота имеет уравнение у = х.

6. Значение f(x₀) называется максимумом функции f(x), если при любом достаточно малом h>0 выполняются условия f(x₀-h)<f(x₀) и f(x₀+h)<f(x₀). Точка х₀ называется в этом случае точкой максимума функции f(x) (рис.5).

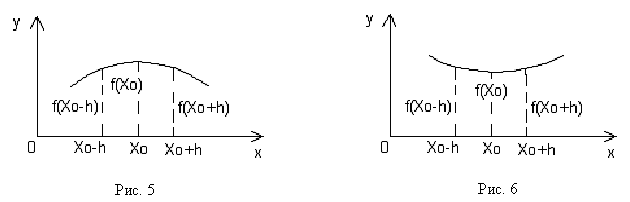
Значение f(x₀) называется минимумом функции f(x), если при любом достаточно малом h>0 выполняются условия f(x₀-h)>f(x₀) и f(x₀+h)>f(x₀). Точка х₀ называется в этом случае точкой минимума функции f(x) (рис. 6).

Максимум или минимум функции называется экстремумом функции.

Необходимое условие экстремума. Если функция f(x) в точке х₀ имеет экстремум, то производная f'(x₀) обращается в нуль или не существует.

Точка х₀, в которой f'(x₀)=0, называется стационарной точкой. Точки, в которых f'(x)=0 или f'(x) не существует, называются критическими точками. Не всякая критическая точка является точкой экстремума.

Функция f(x) называется возрастающей в интервале (a;b), если для любых двух точек х₁и х₂ из указанного интервала, удовлетворяющих неравенству х₁< х₂, выполняется неравенство f(x₁)<f(х₂).Если же f(x₁)>f(х₂) при х₁< х₂, то функция f(x) называется убывающей в интервале (a;b).

Найдем производную данной функции

Найдем критические точки:

х₁=0; х²=12, х₂=

х₂=.

х²≠4, х≠±2 –не входят в область определения функции D(y), значит, экстремума в этих точках быть не может.

Разобьем числовую ось на 5 интервалов, составим таблицу и определим знак первой производной в каждом интервале.

х	-∞;-2	-2	-2;-2	-2;2	2; 2	2	2;+∞
у'(x)	+	0	-	-	-	0	+
у(x)	возрастает	-3	убывает	убывает	убывает	3	возрастает
		max				min

При переходе через точку х = -2 первая производная меняет свой знак с плюса на минус, поэтому в этой точке функция имеет максимум: у_max = у(-2)= -3.

Значит, А(-2;-3) - точка максимума.

При переходе через точку х = -2 первая производная меняет свои знаки с минуса на плюс, поэтому в этой точке функция имеет минимум: у_min = у(2)= 3. Значит, В(2;3) - точка минимума.

7. Достаточное условие выпуклости (вогнутости) графика функции.

Если f''(x)<0 в интервале (a;b), то график функции является выпуклым в этом интервале; если же f''(x)>0, то в интервале (a;b) график функции - выпуклый.

График функции у=f(х) называется выпуклым в интервале (a;b), если он расположен ниже касательной, проведенной в любой точке этого интервала (рис.7).

График функции называется вогнутым в интервале (a;b), если он расположен выше касательной, проведенной в любой точке этого интервала (рис.8).

Точка (х₀;f(х₀)) графика функции, отделяющая его выпуклую и вогнутую части, называется точкой перегиба.

Найдем вторую производную:

y''=0 при х=0 и y'' – не существует при х=±2; которые не входят в область определения функции.

Составим таблицу, разбив числовую ось на интервалы и определим знак второй производной в каждом из них:

х	-∞;-2	-2;0	0	0;2	2;+∞
y''(х)	-	+	0	-	+
у(х)	∩	U		∩	U

На интервалах (-∞;-2) и (0;2) y''<0 и дуга кривой выпукла; на интервалах (-2;0) и (2;+∞), y''>0 и тем самым график является вогнутым.

При переходе через точку х=0 y'' меняет свой знак, поэтому х=0 - абсцисса точки перегиба. Следовательно, С(0;0) – точка перегиба графика функции.

График исследуемой функции показан на рис.9.

Дополнительные точки для построения графика:

х	-3	-5	-1	-1,5
у	-5,4	-5,6		-2