
- •Раздел 4 элементы математического анализа
- •Глава 7. Числовые функции
- •7.1. Определение функции
- •Четность и нечетность.
- •Элементарные функции
- •Степенная функция
- •Показательная функция
- •Логарифмическая функция
- •Тригонометрические функции
- •Обратные тригонометрические функции
- •Преобразование графиков
- •Глава 7
- •Глава 8. Пределы и непрерывность функции
- •8.1. Определение предела функции
- •8.2. Правила раскрытия неопределенностей
- •8.3. Непрерывность функции. Классификация точек разрыва
- •8.4. Второе определение непрерывности
- •Глава 8
8.4. Второе определение непрерывности
Рассмотрим функцию
![]() в некоторой фиксированной точке х
(рис. 8.6). Перейдем
от значения х к другому значению
аргумента
в некоторой фиксированной точке х
(рис. 8.6). Перейдем
от значения х к другому значению
аргумента
![]() ,
при котором функция принимает значение
,
при котором функция принимает значение
![]() .
Точки х и
.
Точки х и
![]() должны принадлежать области определения
функции.
должны принадлежать области определения
функции.
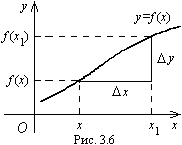
Разность между
новым и первоначальным значением
аргумента называется приращением
аргумента и обозначается
![]() .
.
Разность между
значением функции в новой точке и ее
значением в первоначальной точке
называется приращением функции
и обозначается
![]() .
Поскольку
.
Поскольку
![]() ,
величина
,
величина
![]() .
.
Приращение аргумента
можно задавать произвольно. Приращение
функции
![]() зависит от приращения аргумента Δх
и от точки х. Задав приращение
аргумента Δх, можно вычислить
приращение функции Δy.
зависит от приращения аргумента Δх
и от точки х. Задав приращение
аргумента Δх, можно вычислить
приращение функции Δy.
Пример
8.14. Рассмотрим функцию
![]() в точке
в точке
![]() .
Дадим аргументу х приращение
.
Дадим аргументу х приращение
![]() и перейдем к новой точке
и перейдем к новой точке
![]() ,
,
в которой функция принимает значение
![]() .
.
Приращение функции Δy будет равно
![]() .
.
Запишем условие
непрерывности функции
![]() в точке
в точке
![]() с помощью приращений функции и аргумента.
с помощью приращений функции и аргумента.
Пусть
![]() – некоторая точка, в которой определена
функция
– некоторая точка, в которой определена
функция
![]() .
Перейдем от точки
.
Перейдем от точки
![]() к новой точке х. При этом приращение
аргумента
к новой точке х. При этом приращение
аргумента
![]() ,
приращение функции
,
приращение функции
![]() .
.
Тогда условие
непрерывности функции в точке
![]() можно представить так: если
можно представить так: если
![]() ,
то
,
то
![]() .
Иначе это записывается следующим
образом: если
.
Иначе это записывается следующим
образом: если
![]() ,
то
,
то
![]() .
Так как
.
Так как
![]() ,
а
,
а
![]() ,
определение непрерывности функции
в точке
,
определение непрерывности функции
в точке
![]() можно сформулировать так: функция
можно сформулировать так: функция
![]() называется непрерывной в точке
называется непрерывной в точке
![]() ,
если в этой точке бесконечно малому
приращению аргумента соответствует
бесконечно малое приращение функции.
,
если в этой точке бесконечно малому
приращению аргумента соответствует
бесконечно малое приращение функции.
Свойства функций, непрерывных в точке:
-
если функции
 и
и
 непрерывны в точке
непрерывны в точке
 ,
то их сумма
,
то их сумма
 непрерывна в этой точке;
непрерывна в этой точке; -
если функции
 и
и
 непрерывны в точке
непрерывны в точке
 ,
то их произведение
,
то их произведение
 также непрерывно в точке
также непрерывно в точке
 ;
; -
если функции
 и
и
 непрерывны в точке
непрерывны в точке
 ,
то их отношение
,
то их отношение
 является непрерывной функцией в этой
точке, если знаменатель
является непрерывной функцией в этой
точке, если знаменатель
 не равен нулю в этой точке;
не равен нулю в этой точке; -
если
 и
и
 непрерывные функции, то сложная функция
непрерывные функции, то сложная функция
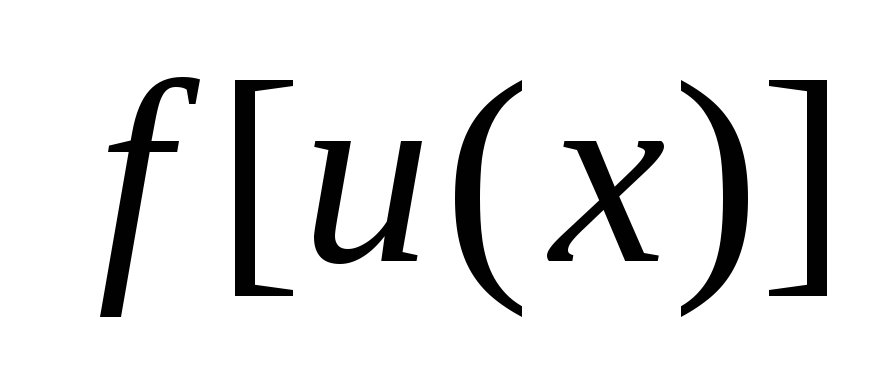 также непрерывна;
также непрерывна; -
всякая элементарная функция непрерывна в своей области определения.
Свойства функций, непрерывных на отрезке:
-
функция, непрерывная на отрезке, ограничена на этом отрезке (рис. 8.7) ВСТАВИТЬ
-
функция, непрерывная на отрезке, имеет на этом отрезке наименьшее значение m и наибольшее значение M (рис.8.8).
-
Если функция непрерывна на отрезке
 и
значения на концах отрезка
и
значения на концах отрезка
 и
и
 имеют противоположные знаки, то внутри
отрезка имеется точка
имеют противоположные знаки, то внутри
отрезка имеется точка
 такая, что
такая, что
 (рис.
8.9).
(рис.
8.9).
Интересно отметить,
что функции, непрерывные на интервале
![]() ,
данными свойствами могут не обладать.
,
данными свойствами могут не обладать.
Например,
функция
![]() на интервале (0; 1) непрерывна, но при x,
стремящемся к нулю справа, неограниченно
возрастает. Функция
на интервале (0; 1) непрерывна, но при x,
стремящемся к нулю справа, неограниченно
возрастает. Функция
![]() непрерывна на интервале (0; 1), но не имеет
на этом интервале ни наименьшего, ни
наибольшего значения.
непрерывна на интервале (0; 1), но не имеет
на этом интервале ни наименьшего, ни
наибольшего значения.
УПРАЖНЕНИЯ
Найти пределы функции при различных значениях а.
8.15.
![]() ,
1)
,
1)
![]() ;
2)
;
2)
![]() ;
3)
;
3)
![]() .
.
8.16.
![]() ,
1)
,
1)
![]() ;
2)
;
2)
![]() ;
3)
;
3)
![]() .
.
8.17.
![]() ,
1)
,
1)
![]() ;
2)
;
2)
![]() ;
3)
;
3)
![]() .
.
8.18.
![]() ,
1)
,
1)
![]() ;
2)
;
2)
![]() ;
3)
;
3)
![]() .
.
8.19.
![]() ,
1)
,
1)
![]() ;
2)
;
2)
![]() ;
3)
;
3)
![]() .
.
8.20.
![]() ,
1)
,
1)
![]() ;
2)
;
2)
![]() ;
3)
;
3)
![]() .
.
8.21.
![]() .
.![]() 8.22.
8.22.
![]() .
8.23.
.
8.23.
![]() .
8.24.
.
8.24.
![]() .
8.25.
.
8.25.
![]() .
8.26.
.
8.26.
![]() .
8.27.
.
8.27.
![]() .
8.28.
.
8.28.
![]() . 8.29.
. 8.29.
![]() .
8.30.
.
8.30.
![]() .
8.31.
.
8.31.![]() .
8.32.
.
8.32.
![]() .
8.33.
.
8.33.
![]() .
8.34.
.
8.34.
![]() .
8.35.
.
8.35.
![]() .
8.36.
.
8.36.
![]() .
8.37.
.
8.37.
![]() .
8.38.
.
8.38.
![]() .
8.39.
.
8.39.
![]() .
8.40.
.
8.40.
![]() .
8.41.
.
8.41.
![]() .
8.42.
.
8.42.
![]() .
8.43.
.
8.43.
![]() .
8.44.
.
8.44.
![]() .
8.45.
.
8.45.
![]() .
8.46.
.
8.46.
![]() .
8.47.
.
8.47.
![]() .
8.48.
.
8.48.
![]() .
8.49.
.
8.49.
![]() .
8.50.
.
8.50.
![]() .
8.51.
.
8.51.
![]() .
8.52.
.
8.52.
![]() .
8.53.
.
8.53.
![]() .
8.54.
.
8.54.
![]() .
8.55.
.
8.55.
![]() .
8.56.
.
8.56.
![]() .
8.57.
.
8.57.
![]() .8.58.
.8.58.
![]() .
8.59.
.
8.59.
![]() .
8.60.
.
8.60.
![]() .
8.61.
.
8.61.
![]() .
8.62.
.
8.62.
![]() .
8.63.
.
8.63.
![]() .
8.64.
.
8.64.
![]() .
.
Вычислить односторонние пределы функций.
8.65.
а)![]() ;
б)
;
б)
![]() .
8. 66. а)
.
8. 66. а)
![]() ;
б)
;
б)
![]() .
8.67. а)
.
8.67. а)![]() ;
б)
;
б)
![]() .
8.68. а)
.
8.68. а)
![]() ;
б)
;
б)
![]() .
8.69. а)
.
8.69. а)![]() ;
б)
;
б)
![]() .
8.70.
.
8.70.
![]() , где
, где
![]() .
8.71.
.
8.71.
![]() .
8.72. а)
.
8.72. а)
![]() ;
б)
;
б)
![]() .
.
Найти точки разрыва и построить график функций.
8.73.![]() .
8.74.
.
8.74.
![]() 8.75.
8.75.
 8.76.
8.76.
![]() . 8.77.
. 8.77.
![]() .
8.78.
.
8.78.
![]() .
8.79.
.
8.79.
![]() .
8.80.
.
8.80.
![]() 8.81.
8.81.
 8.82.
8.82.
 8.83.
8.83.
 8.84.
8.84.
![]() 8.85.
8.85.
 8.86.
8.86.
![]() . 8.87.
. 8.87.
![]() 8.88.
8.88.
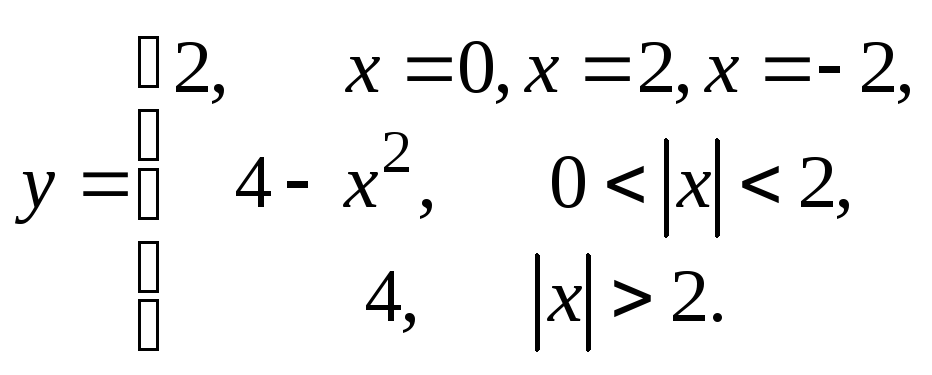
Исследовать данные функции на непрерывность в указанных точках.
8.89.
![]()
![]()
![]() 8.90.
8.90.
![]()
![]()
![]() 8.91.
8.91.
![]()
![]()
![]()
О Т В Е Т Ы К У П Р А Ж Н Е Н И Я М
