
- •Содержание
- •Математическое моделирование систем управления
- •Основные понятия
- •Математическое описание динамики сар
- •Аналитическое построение математической модели
- •Задачи проектирования многомерных систем управления
- •Преобразование Лапласа. Понятие передаточной функции
- •Типовые воздействия
- •Типовые звенья обыкновенных линейных систем
- •Идеальное интегрирующее звено (интегратор)
- •Идеальное дифференцирующее звено
- •Неидеальное интегрирующее звено
- •Дифференцирующее инерционное звено
- •Идеальное форсирующее звено
- •Апериодическое звено первого порядка
- •Колебательное звено
- •Топология систем управления. Способы соединения элементов
- •Последовательное соединение
- •Соединение с обратной связью
- •Вычисление передаточных функций
- •Свободное и вынужденное движение
- •Характеристическое уравнение. Понятие корневого годографа
- •Построение частотных характеристик
- •Методы анализа качества систем управления
- •Понятие устойчивости систем управления
- •Критерии устойчивости Гурвица и Рауса (алгебраические)
- •Критерии устойчивости Михайлова и Найквиста (частотные)
- •Корневые показатели качества
- •Анализ качества сау по переходной характеристике
- •Анализ качества сау по частотным характеристикам
- •Статические и астатические системы
- •Основы оптимизации и методы синтеза систем управления
- •Постановка задачи параметрической оптимизации
- •Методика решения задачи параметрической оптимизации
- •Синтез адаптивных систем управления
- •4.1.Постановка задачи синтеза самонастраивающихся систем
- •Процедура синтеза закона управления
- •Синтез адаптивного управления при помощи пи- регулятора
- •Экстремальные системы управления
- •Оптимальное управление
- •Аналитическое конструирование регулятора
- •Дискретные и цифровые системы управления
- •Общие сведения
- •Модели дискретных процессов
- •Квантование непрерывных сигналов и теорема прерывания
- •Использованиеz- преобразования
- •Устойчивость и качество дискретных систем
- •Цифровые системы управления
- •Отдельные вопросы теории управления
- •Управляемость и наблюдаемость
- •Инвариантные системы управления
- •Расчет и анализ чувствительности
- •Робастные системы управления
- •Литература
Основы оптимизации и методы синтеза систем управления
Постановка задачи параметрической оптимизации
Пусть поведение одномерной системы управления описывается дифференциальным уравнением вида:
|
B(p) y(t) = A(p) g(t), p = d / dt |
(3.1) |
![]() .
.
B(p)– операторная функция преобразования. Аналогично можно записать операторную функциюA(p).Особого внимания заслуживает рассмотрение преобразования входного сигналаg(t)в выходнойy(t):
|
|
(3.2) |
![]() –ядро операторного
преобразования. Если в системе управления
выделить вектор варьируемых параметров
х, то последняя формула примет вид:
–ядро операторного
преобразования. Если в системе управления
выделить вектор варьируемых параметров
х, то последняя формула примет вид:
|
|
(3.3) |
Пусть на качество САУ наложены ограничения вида:
|
|
(3.4) |
|
|
(3.5) |
|
|
h |
(3.6) |
Здесь приняты
следующие обозначения:
![]() - абсолютное значение величины
перерегулирования;
- абсолютное значение величины
перерегулирования;![]() -
статическая ошибка;h(x,t)- переходная характеристика;h
(х, t
-
статическая ошибка;h(x,t)- переходная характеристика;h
(х, t![]() )- установившееся значение переходного
процесса;
)- установившееся значение переходного
процесса;![]() -
требуемое значение выходной (управляемой)
переменной.
-
требуемое значение выходной (управляемой)
переменной.
Задача параметрической оптимизации для одномерной САУ, поведение которой описывается уравнением (3.3), состоит в определении таких значений компонент вектора x, принадлежащих заданной области, при которых САУ будет обладать требуемыми характеристиками. Решение задачи сложный и трудоемкий процесс, часто с трудно разрешимыми ситуациями. «Метод проб и ошибок» в поиске рациональных параметров не является эффективным. Рассмотрим решение на основе моделирования процессов в комплексной плоскости. В качестве модели САУ будем рассматривать модель вида:
|
Y(x,s) =W(x,s)
*G(s), |
(3.7) |
Воспользуемся доказанным утверждением [6]. Для выполнения условий (3.4) - (3.6), налагаемых на качество управления во временной области, достаточно выполнение следующих условий в комплексной плоскости:
|
| sY(x,s)
- |
(3.8) |
|
s, (=+j:-,> 0, |||| ).
|
(3.9) |
В связи с этим
задача параметрической оптимизации
может быть переформулирована следующим
образом. Для САУ, поведение которой
описывается уравнением (3.7), требуется
найти такие значения компонент вектора
оптимизируемых параметров х = хопт.,
при которых система управления будет
обладать требуемым качеством (3.8) –
(3.9) за счет максимального приближения
к эталоной системе управления, чтобы
целевая функцияF(x),характеризующая такое приближение,
принимала минимальное значение![]() .
.
Методика решения задачи параметрической оптимизации
Прежде чем перейти к решению задачи, рассмотрим влияние полюсов и нулей на статические и динамические характеристики системы управления.
Запишем выражение установившегося процесса на выходе одномерного объекта управления:
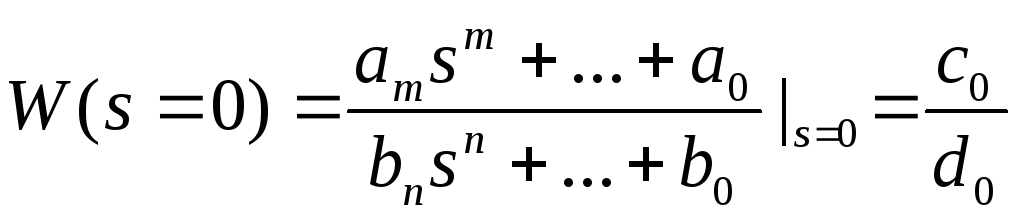 .
.
Отметим, что если нуль и полюс находятся близко друг к другу, а именно: на расстоянии менее чем 0.1 модуля, то влияние такого полюса ослабляется нулем, то есть полюс не оказывает существенного влияния на динамические характеристики системы управления. Рассмотрим пример. Пусть выходная функция Y(s)имеет вид:
![]() ,
( s1п = - 5.2,s2п
= - 8,s1н =
-5).
,
( s1п = - 5.2,s2п
= - 8,s1н =
-5).
Поскольку расстояние между нулем и первым полюсом намного меньше модуля корня, то влиянием ближайшего к нулю полюса можно пренебречь, так как он оказывает несущественное влияние на динамику системы управления в целом. Рассмотрим ситуацию, когда многомерная система управления, описываемая системой уравнений (3.8), не удовлетворяет требованиям качества, это означает, что некоторые полюсы выходят за границу области или нули оказывают отрицательное влияние на качество управления. Идеальной системой управления будем считать такую систему, которая имеет заданное расположение полюсов и нулей или заданный корневой годограф. Для решения задачи параметрической оптимизации введем в рассмотрение расположение идеальных полюсов и нулей. Известные формулы перехода от корней алгебраического уравнения к его коэффициентам позволяют найти передаточную функцию эталоной системы управления вида:
|
|
(3.10) |
Передаточная функция оптимизируемой по параметрам системы управления может быть представлена в виде:
|
|
(3.11) |
Таким образом, имеем эталоную передаточную функцию в виде (3.10) и реальную в виде (3.11). Метод параметрической оптимизации основан на приближении реальной системы управления к эталоной как можно ближе за счет оптимальной настройки параметров x. Введем в рассмотрение оптимизируемую функцию как средне - квадратичную ошибку аппроксимации по коэффициентам передаточных функций эталоной и оптимизируемой по параметрам систем управления. Целевая функция примет вид:
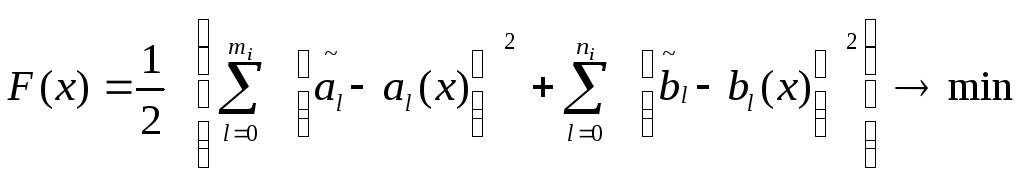
Здесь приняты
следующие обозначения: al(x),
![]() -соответственно коэффициенты полиномовA(x,s)и
-соответственно коэффициенты полиномовA(x,s)и![]() ;bl(x),
;bl(x),![]() -
соответственно коэффициенты полиномовB(x,s)и
-
соответственно коэффициенты полиномовB(x,s)и![]() .
ФункцияF(x)– алгебраическая. Для нахождения ее
минимума на множествеX,
заданном ограничениями вида:l(х)
= 0, (l=
.
ФункцияF(x)– алгебраическая. Для нахождения ее
минимума на множествеX,
заданном ограничениями вида:l(х)
= 0, (l=![]() ),
воспользуемся подходом основанным на
введении неопределенных множителей
Лагранжа
),
воспользуемся подходом основанным на
введении неопределенных множителей
Лагранжа![]() [2], что предполагает решение системы
уравнений вида:
[2], что предполагает решение системы
уравнений вида:
|
|
(3.12) |
где k- размерность вектора![]() .
Первые уравнения вытекают из приравнивания
к нулю производных функцииФ(x,
)по переменным вектора.Минимум функцийF(x)иФ(x, )будет достигнут в точкеx
= xопт,
найденной из решения (3.13), если в этой
точке будет выполнено условие
положительности квадратичной формы (
условие Вейерштрасса):
.
Первые уравнения вытекают из приравнивания
к нулю производных функцииФ(x,
)по переменным вектора.Минимум функцийF(x)иФ(x, )будет достигнут в точкеx
= xопт,
найденной из решения (3.13), если в этой
точке будет выполнено условие
положительности квадратичной формы (
условие Вейерштрасса):
|
|
(3.13) |
где
![]() xi,
xi,![]() xj- малые приращения компонент векторах. Следовательно, чтобыx
= xоптбыла
точкой, в которой целевая функция
принимает минимальное значение,
необходимо и достаточно, чтобы в этой
точке выполнялись условия (3.12) и (3.13).
Для решения (3.12) используются известные
методы, в частности, численный метод
решения системы нелинейных алгебраических
уравнений Ньютона - Рафсона. Отметим,
что любые неравенства, накладываемые
на неизвестные параматры векторах,
можно привести к равенствам, вводя
дополнительные неизвестные. Например,
пусть имеем ограничение вида: х
xj- малые приращения компонент векторах. Следовательно, чтобыx
= xоптбыла
точкой, в которой целевая функция
принимает минимальное значение,
необходимо и достаточно, чтобы в этой
точке выполнялись условия (3.12) и (3.13).
Для решения (3.12) используются известные
методы, в частности, численный метод
решения системы нелинейных алгебраических
уравнений Ньютона - Рафсона. Отметим,
что любые неравенства, накладываемые
на неизвестные параматры векторах,
можно привести к равенствам, вводя
дополнительные неизвестные. Например,
пусть имеем ограничение вида: х![]() <5,
которое можно переписать в виде: х
<5,
которое можно переписать в виде: х![]() =5
- х
=5
- х![]() ,
где х
,
где х![]() дополнительно вводимый параметр,
подлежащий определению наравне с
остальными параметрами векторах.
дополнительно вводимый параметр,
подлежащий определению наравне с
остальными параметрами векторах.
Рассмотрим применение методики параметрической оптимизации на конкретной задаче.
Проектирование САР с ПИД - регулятором в контуре управления.
Пусть задана схема управления в виде:
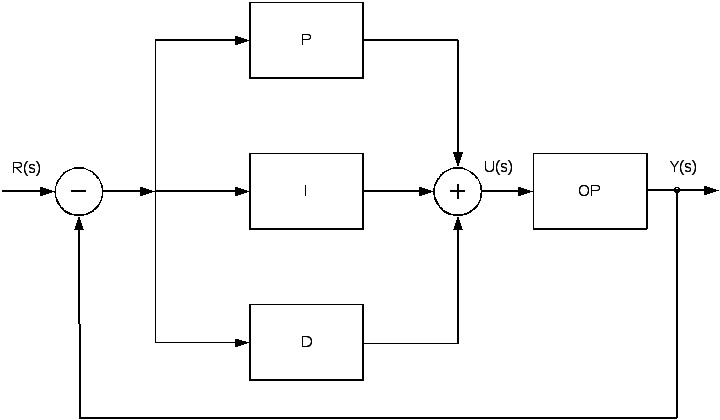
В схеме известен вид передаточных функций звеньев:
Wp = kp; W i= ki /s; Wd = kd s; Wор (s) = k / (s + a).
Нужно найти значения
вектора параметров x
= (kp,
ki,
kd),при которых корниsiхарактеристического уравнения замкнутой
системы будут принадлежать области
качества,
определяемой параметрами
= 2,
![]() 1. Решение будем строить по шагам:
1. Решение будем строить по шагам:
Найдем передаточную функцию разомкнутой системы управления:
Wраз. (x, s) = (kp + ki/s + kds) k /(s + a) = k(skp + ki + kds2)/(s(s +a)).
Определим передаточную функцию замкнутой системы:
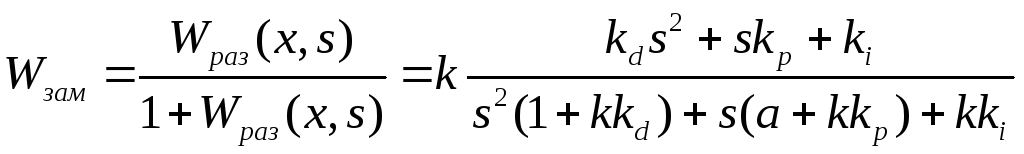 .
.
Запишем характеристическое уравнение замкнутой системы:
![]() .
.
4. Зададим эталоное расположение корней характеристического уравнения
и по ним составим характеристическое уравнение:
![]() ,
,
![]() =s2+ 5s+ 6 = 0.
=s2+ 5s+ 6 = 0.
Cоставим целевую функциюF(x)на основе минимизации невязок коэффициентов двух характеристических уравнений:
![]() .
.
Отметим, что поскольку на параметры вектора хне наложены ограничения, то имеем дело с задачей безусловной оптимизации. Для достижения минимума положительной квадратичной функцииF(x)достаточно, чтобы нулю равнялись все три слагаемые, а именно:
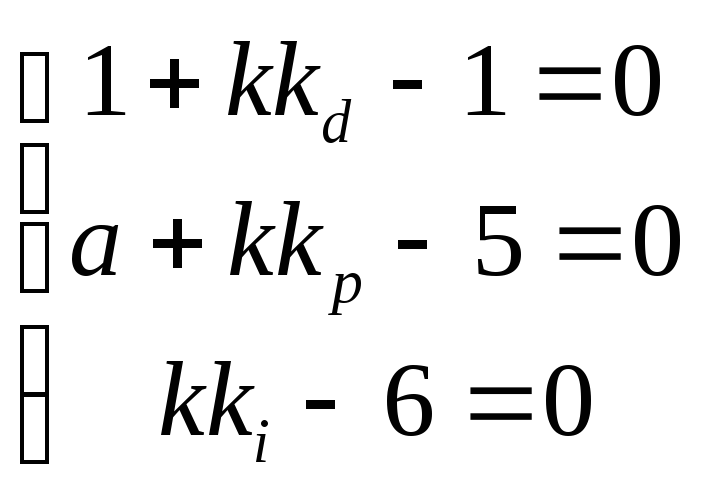
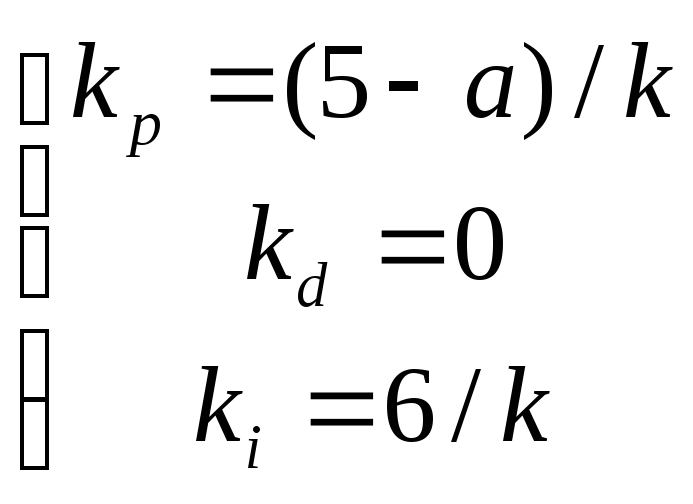
Если мы используем необходимое и достаточное условие минимальности F(x), то получаем следующую систему уравнений:

Поскольку оптимизируемая функция является положительной квадратичной, она имеет один экстремум – минимум и, следовательно, нет необходимости проверять условие Вейерштрасса, то есть положительность квадратичной формы.
Рассмотрим алгоритм параметрической оптимизации для многомерной САУ. Его применение предполагает выполнение следующих этапов:
Задание схемы САУ, передаточных функций звеньев, вектора оптимизируемых параметров х, ограничений(x),начального значения
х = х0.
Выполнение декомпозиции схемы на каналы вход - выход.
Нахождение матрицы W(x,s).
Анализ качества системы управления по расположению нулей и полюсов матрицы W(x,s) при х = х0. Если качество удовлетворительно, то нужно перейти к п.9.
Задание эталоной системы управления в виде
 .
.Формирование целевых функций Ф(x,), F(x).
Решение задачи оптимизации для Ф(x,) min илиF(x) min.
Вывод результатов в виде значений вектора х.
Конец алгоритма.
При автоматизации производственных процессов возникает задача выбора типового регулятора и определение его параметров, обеспечивающих заданное качество управления объектом. При этом обычными приемами синтеза регулятора являются: выбор закона регулирования в виде уравнений динамики регулятора; определение передаточной функции САР; исследование САР на устойчивость; определение параметров настройки регулятора в соответствии с требованиями, налагаемыми на качество управления. Если не удается настроить параметры регулятора должным образом, то проектирование продолжается в направлении усложнения регулятора. Под сложностью регулятора понимают порядок его уравнений. Обычно сложность регулятора не превышает сложности объекта регулирования.


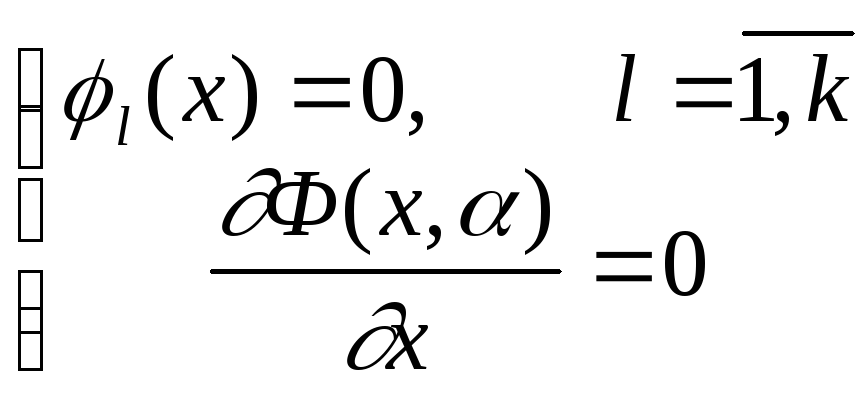 Ф(x,)
=F(x)+
Ф(x,)
=F(x)+