3.3. Типовые динамические звенья и их передаточные функции

Согласно теореме Виета полином n-го порядка может быть представлен в виде произведения двучленов, а поэтому передаточная функция системы примет вид:

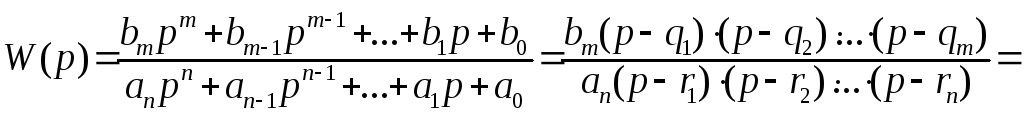
= kW_Э1(p)  W_Э2(p)  ...  W_ЭK(p), (3.29)

где q_i - корни полинома числителя W(p), называемые ее нулями, r_i - корни полинома знаменателя W(p), называемые ее полюсами (напомним, что полюса передаточной функции системы есть корни характеристического уравнения этой же системы); k=^b0/a₀.

Выражение (3.29) показывает, что любую систему можно представить в виде соединения элементарных звеньев, которые принято называть типовыми динамическими звеньями. Каждое типовое динамическое звено имеет один вход, один выход, обладает свойством однонаправленности передачи входного воздействия и имеет порядок не выше второго.

Передаточные функции типовых динамических звеньев.

а) Безынерционное усилительное звено

x(t) = k f(t); X(p) = k F(p); W(p) = X(p)/F(p) = к . (3.30)

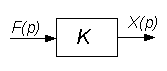
Рис.3.2. Структурная схема усилительного звена:

б) Интегрирующее звено

k_и f(t); x(t) = k_и;

X(p) = (k_и/p) F(p); W(p) = X(p)/F(p) = k_и/p или, если принять, что 1/к_и=Т_и - постоянная времени интегрирующего звена, то

W(з)=1/Т_ир (3.31)

Характеристическое уравнение p = 0, т.е. p₁= 0.

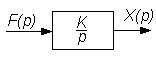
Рис.3.3. Структурная схема интегрирующего звена:

В) Идеальное дифференцирующее звено

x(t) = k_д;

X(p) = k_д p F(p);

W(p) = X(p)/F(p) = k_д p=Т_др, (3.32)

где к_д=Т_д – постоянная времени дифференцирующего звена.

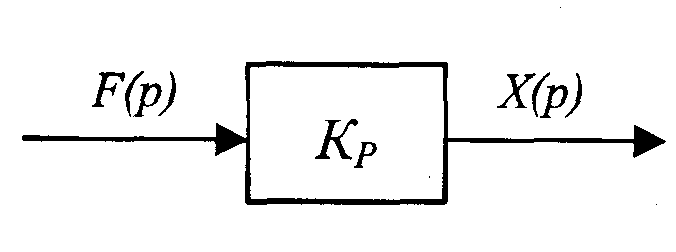
Рис.3.4. Структурная схема идеального дифференцирующего звена

г) Апериодическое звено (инерционное звено первого порядка)

T + x(t) = 1 f(t);

(T p + 1) X(p) = 1 F(p);

W(p) = X(p)/F(p) = 1/(T p + 1). (3.33)

Характеристическое уравнение: T p + 1 = 0;

p₁= -1/T, где Т – постоянная времени апериодического звена.

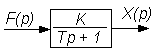
Рис.3.5. Структурная схема апериодического звена

д) Форсирующее звено

, (3.34)

где Т_ф – постоянная времени форсирующего звена.

Рис.3.6. Структурная схема форсирующего звена

е) Динамическое звено второго порядка

+ 2T₀  + x(t) = 1 f(t);

( p²+2T₀ p + 1) X(p) = 1 F(p);

W(p) = X(p)/F(p) = 1/( p²+2T₀ p + 1). (3.35)

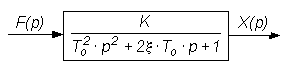
Рис.3.7. Структурная схема звена

Характеристическое уравнение

 p²+2T₀ p + 1= 0;

p_1,2 = , (3.36)

т.е. значения и характер корней характеристического уравнения зависят от величины коэффициента относительного затухания .

При >1 корни характеристического уравнения (см. (3.36)) являются вещественными, и поэтому передаточную функцию рассматриваемого звена можно представить в следующем виде:

, (3.37)

где . (3.38)

В этом случае звено второго порядка эквивалентно по своим динамическим свойствам последовательному соединению двух инерционных звеньев первого порядка и называется инерционным звеном второго порядка.

При 0< < 1 корни характеристического уравнения

p_1,2 = -  j,

где , (3.39)

т.е. корни комплексно-сопряженные, а звено называется колебательным.

При  = 0 передаточная функция колебательного звена примет вид

W(p) = 1/( p² + 1). (3.40)

Корни характеристического уравнения

 p²+1= 0;

p_1,2 = , (3.41)

являются мнимыми сопряженными, а звено называется консервативным.

Рассмотренные передаточные функции и корни характеристических уравнений показывают, что звено второго порядка может обладать разными динамическими свойствами.