Локальная интерполяция Кусочно-постоянная интерполяция

При кусочно-постоянной интерполяции интерполяционный многочлен на каждом отрезке равен константе, а именно, левому или правому значению функции.

Для левой кусочно-постоянной интерполяции , если , т.е.

.

Для правой кусочно-постоянной интерполяции , если , т.е.

.

Легко понять, что при таком выборе функции условия интерполяция выполняются. Однако, построенная функция является разрывной, что ограничивает ее применение. Графическое представление для кусочно-постоянной интерполяции можно увидеть на рис. 3.1.

Рис. 3.1. Левая (а) и правая (б) кусочно–постоянная интерполяции

Кусочно-линейная интерполяция

На каждом интервале интерполирующая функция является линейной . Значения коэффициентов и находятся из выполнения условий интерполяции на концах отрезка : , . С помощью этих условий получаем систему уравнений:

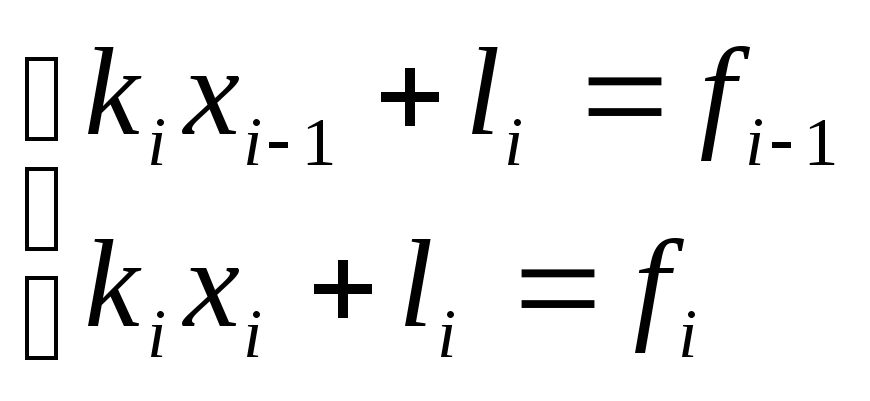, откуда находим , . Следовательно, функцию можно записать в виде:

, если , т.е.

.

При использовании линейной интерполяции сначала нужно определить интервал, в который попадает значение , а затем подставить его в формулу.

Итоговая функция является непрерывной, но ее производная разрывна в каждом узле интерполяции. Погрешность такой интерполяции будет меньше, чем в случае кусочно-постоянной интерполяции. Иллюстрация кусочно-линейной интерполяции приведена на рис. 3.2.

Рис. 3.2. Кусочно-линейная интерполяция

ПРИМЕР 3.1 Заданы значений некоторой функции:

	0	2	3	3,5
	-1	0.2	0,5	0,8

Требуется найти значение функции при и при помощи кусочно-постоянной и кусочно-линейной интерполяции.

Решение. Точка принадлежит первому отрезку , т.е. и, следовательно, по формулам левой кусочно-постоянной интерполяции , по формулам правой кусочно-постоянной интерполяции . Теперь воспользуемся формулами кусочно-линейной интерполяции:

, ,

и тогда .

Точка принадлежит третьему интервалу , т.е. и, следовательно, по формулам левой кусочно-постоянной интерполяции , по формулам правой кусочно-постоянной интерполяции . Воспользуемся формулами кусочно-линейной интерполяции:

, , и .

Кубический интерполяционный сплайн

Слово сплайн, происходящее от английского слова spline, означает гибкую линейку, используемую для проведения гладких кривых через заданные точки на плоскости. Форма этого универсального лекала на каждом отрезке описывается кубической параболой. Сплайны широко используются в инженерных приложениях, в частности, в компьютерной графике, поскольку позволяют с хорошей точностью задать кривые в виде нескольких массивов коэффициентов.

Итак, на каждом -м отрезке , , решение будем искать в виде полинома третьей степени:

Неизвестные коэффициенты , , находим из:

• условий интерполяции: , , ;

• непрерывности функции ,;

• непрерывности первой и второй производной:

, , .

Учитывая, что ,

для определения неизвестных получаем систему уравнений:

, ;

, ;

, ;

, ,

где _. Недостающие два уравнения выводятся из дополнительных условий: . Можно показать, что при этом . Из системы можно исключить неизвестные , , получив систему линейных уравнений (СЛАУ) для определения коэффициентов :

, ,

, (3.1)

Матрица СЛАУ (3.1) является ленточной, поэтому система решается с помощью прямого экономичного метода прогонки. После этого вычисляются коэффициенты , :

, , . (3.2)

В случае постоянной сетки , и тогда система уравнений упрощается:

Для вычисления значения в произвольной точке отрезка необходимо решить систему уравнений на коэффициенты , , затем найти все коэффициенты , . Далее, необходимо определить, на какой интервал попадает эта точка, и, зная номер , вычислить значение сплайна и его производных в точке

,

,

.

ПРИМЕР 3.2. Задана таблица значений функции

	0	1/4	1/2	3/4	1
f	1	2	1	0	1

Требуется вычислить значения функции в точках 0,2 и 0,8, используя сплайн-интерполяцию.

В нашем случае: , .

Выпишем систему уравнений для определения :

.

Решая эту систему линейных уравнений, получим:

.

, ,

, .

,

,

,

,

.

Рассмотрим точку 0,2, которая принадлежит первому отрезку, т.е. . Следовательно, получим,

Итак, значение функции в точке 0,2 равняется 1,944.

Рассмотрим точку 0.8, которая принадлежит четвертому отрезку, т.е. .

Следовательно,