Примеры решения задач и рекомендации к экзамену

Задача 1. Получить решение уравнения методом деления отрезка пополам с точностью 0,05. Интервал изоляции .

Проверим, что данных отрезок является интервалом изоляции корня. Найдем значение функции на концах этого интервала: , . Т.е. на интервале содержится корень уравнения. Проверим, что он единственный.

Следовательно, на всем интервале , а , т.е. функция монотонно возрастающая на , следовательно, данный интервал содержит один корень уравнения и является интервалом изоляции.

Расчеты проведем в Excel по методу деления отрезка пополам, результаты оформим в виде таблицы.

0	-4	-3.8	-3.9	-3	-0.009	0.2
1	-3.9	-3.8	-3.85	-0.009	1.405875	0.1
2	-3.9	-3.85	-3.875	-0.009	0.705078	0.05
3	-3.9	-3.875	-3.8875	-0.009	0.349705	0.025

Расчетные формулы:

Ответ: x=-3.8875

Задача 2. Получить решение уравнения методом простой итерации с точностью 0.001. Интервал изоляции .

Аналогично доказываем, что интервал является интервалом изоляции.

,

на всем интервале , а , т.е. функция монотонно возрастающая на , следовательно, данный интервал является интервалом изоляции.

Расчетные формулы:

Найдем значения констант. Для этого вычислим значения первой и второй производных:

.

Экстремум производной функции находится в точке

.

Находим значения производной на концах отрезка

.

Таким образом, .

, .

Вычисления оформляем в таблице

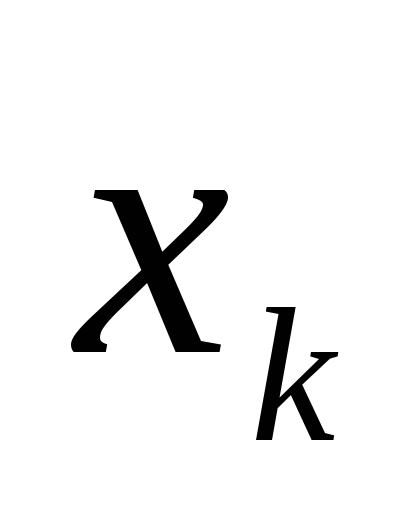
0	-4	-3
1	-3.9118	-0.35069	0.0882
2	-3.90149	-0.05198	0.01031
3	-3.89996	-0.0079	0.001528
4	-3.89973	-0.0012	0.000232

Ответ: x= -3,8997

Задача 3. Получить решение уравнения методом Ньютона с точностью 0,001. Интервал изоляции .

Проверка значений интервала изоляции была сделана в примере выше. Расчетные формулы метода Ньютона:

или в нашем случае

Выбираем нулевое приближение. , , . Знак функции и знак второй производной совпадают на правом конце отрезка, поэтому выбираем его в качестве начального приближения .

Результаты представлены в таблице

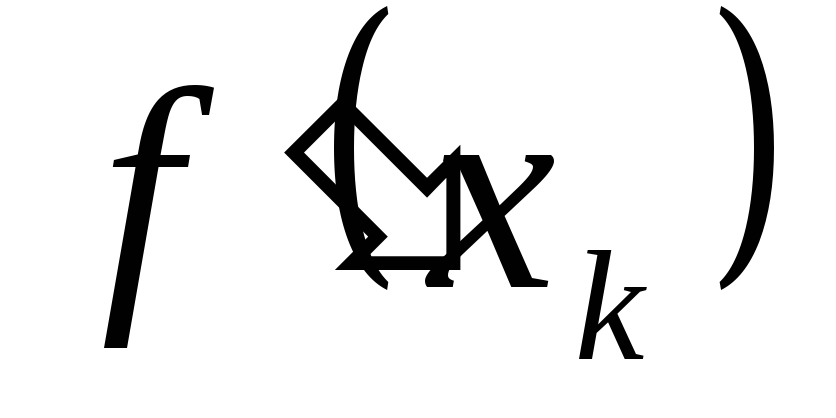
0	-5	-46	56
1	-4.17857	-8.89217	35.02423	0.821429
2	-3.92469	-0.72721	29.36009	0.253886
3	-3.89992	-0.00659	28.82821	0.024769
4	-3.89969	-5.6E-07	28.82332	0.000229

Ответ: x=-3,89969

Задача 4. Решить систему линейных уравнений методом простой итерации с точностью 0,05:

Проверим условие диагонального преобладания:

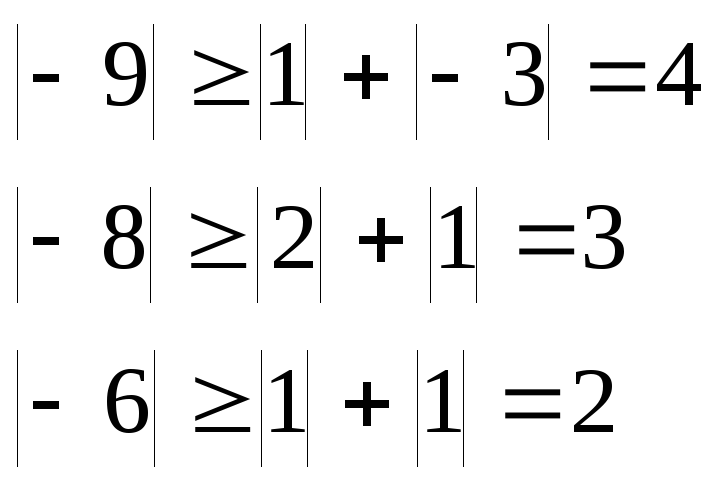
Условия диагонального преобладания выполняются.

Разрешим систему уравнений относительно

Результаты можно представить в виде таблицы

0	0	0	0	–
1	-0.33333	-0.125	-1	1
2	-0.01389	-0.33333	-1.07639	0.319444
3	-0.01157	-0.26302	-1.05787	0.070313
4	-0.00993	-0.26013	-1.04577	0.012105

Ответ содержится в последней строке таблицы.

Задача 5. Решить систему линейных уравнений методом Гаусса-Зейделя с точностью 0,05:

Аналогично проверяем условие диагонального преобладания.

Разрешим систему уравнений относительно

Результаты удобно оформить в таблицу

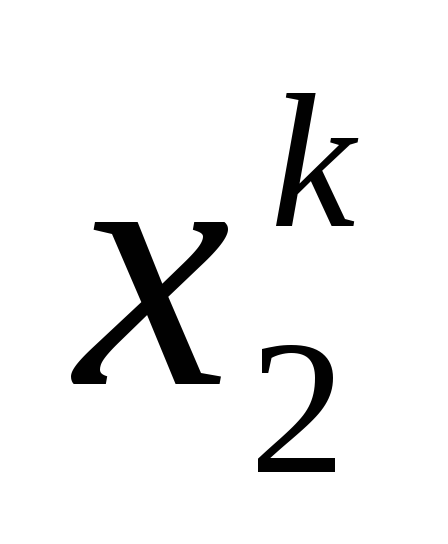
0	0	0	0
1	-0.33333	-0.20833	-1.09028	1.090278
2	0.006944	-0.25955	-1.0421	0.340278
3	-0.01481	-0.25896	-1.04563	0.02175

Ответ содержится в последней строке таблицы.

Задача 6. Для таблично заданной функции:

	-2	1	1,5	2
	0,1	-0,2	0,5	1,2

вычислить значение функции в точке z=1,2, используя формулы линейной интерполяции.

Определяем интервал, которому принадлежит : .

Расчетные формулы:

.

Тогда

.

Ответ: 0,08.

Задача 7. Для таблично заданной функции:

	-2	1	1,5	2
	0,1	-0,2	0,5	1,2

выписать базисные полиномы и вычислить значение полинома Лагранжа в точке z=1,2; при n=3.

Ответ: 0,0748.

Примеры решения задач на интегрирование можно найти выше.

Рекомендации. В билетах задание может быть в виде:

Вычислить интеграл методом трапеций функции, заданной таблично:

	-1	-0,5	0	1
	2	3	4	4,5

В данном задании переменная меняется с постоянным шагом 0,5. При использовании формулы трапеций решение ищется в виде:

.

В случае же, если шаг не постоянный, например:

	-1	-0,6	0	0,8
	2	3	4	4,5

необходимо пользоваться общей формулой трапеций:

Т.е. в данном случае решение ищется как

Аналогично для формул левых и правых прямоугольников:

.

ВВЕДЕНИЕ 3

ПРИБЛИЖЕННОЕ РЕШЕНИЕ НЕЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ 5

МЕТОДЫ РЕШЕНИЯ СИСТЕМ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ 23

АППРОКСИМАЦИЯ ФУНКЦИЙ 43

ЧИСЛЕННОЕ ИНТЕГРИРОВАНИЕ 64

ЧИСЛЕННОЕ РЕШЕНИЕ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ 74

МЕТОД КОНЕЧНЫХ РАЗНОСТЕЙ РЕШЕНИЯ КРАЕВЫХ ЗАДАЧ ДЛЯ ОДУ 85

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ И РЕКОМЕНДАЦИИ К ЭКЗАМЕНУ 94

101