Линейная алгебра

Матрицы

Определение 1

Упорядоченный набор элементов называется матрицей. Обычно матрицу записывают в виде таблицы

Определение 2

Упорядоченный набор элементов называется -той строкой матрицы.

Определение 3

Упорядоченный набор элементов называется -тым столбцом матрицы.

Определение 4

Говорят, что матрица имеет размерность если она состоит из элементов . Обозначается матрица или

Определение 5

Матрица размерности называется матрицей-строчкой . При этом обычно для матрицы строчки опускают первый индекс, т.е. пишут .

Определение 6

Матрица размерности называется матрицей-столбцом 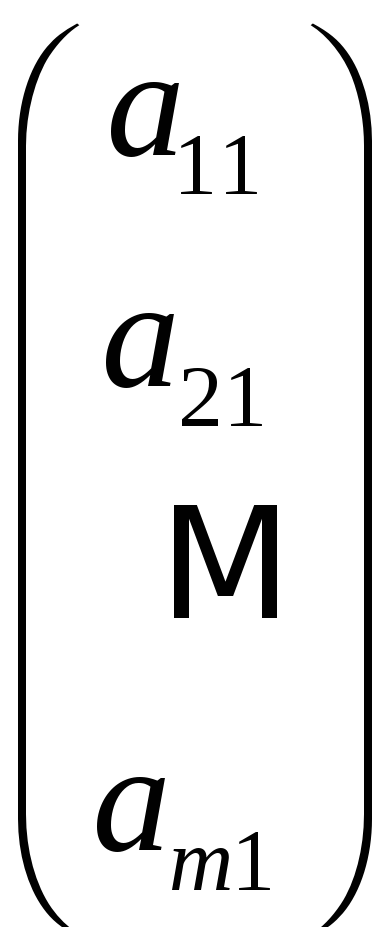При этом обычно для матрицы-столбца опускают второй индекс Для экономии места матрицу-столбец 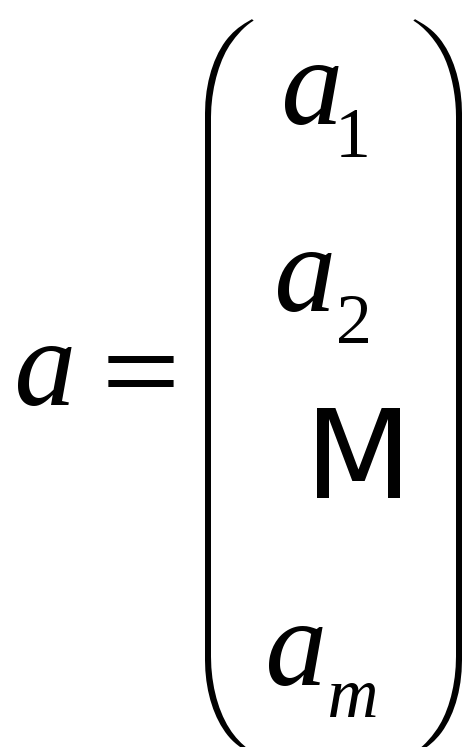записывают либо либо обозначают .

Таким образом матрицу 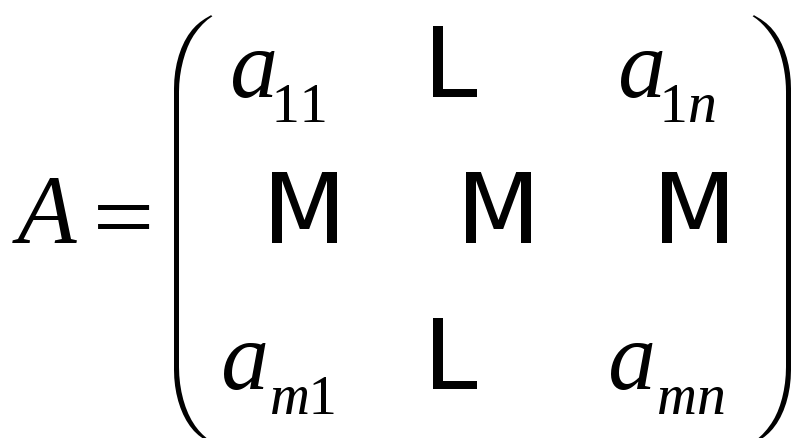можно записать 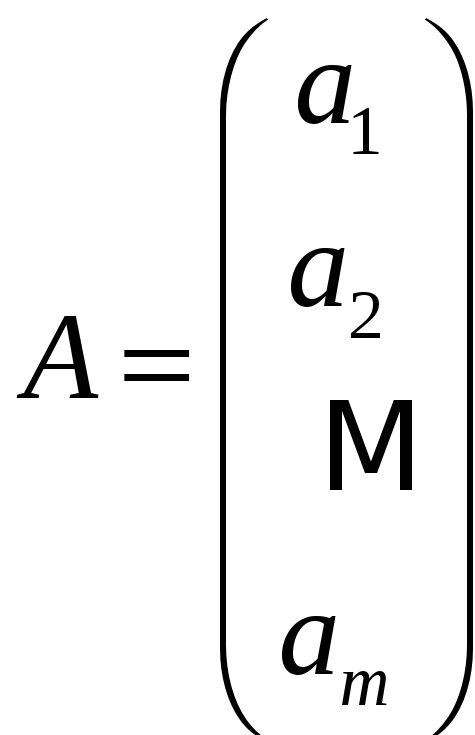, где - матрица-строчка или , где - матрица-столбец .

Определение 7

Матрица размерности называется квадратной матрицей порядка .

При дальнейшем изложении будем всегда подразумевать, что элементы матрицы это числа (действительные, комплексные).

Определение 8

Квадратная матрица такая, что называется нулевой матрицей порядка .

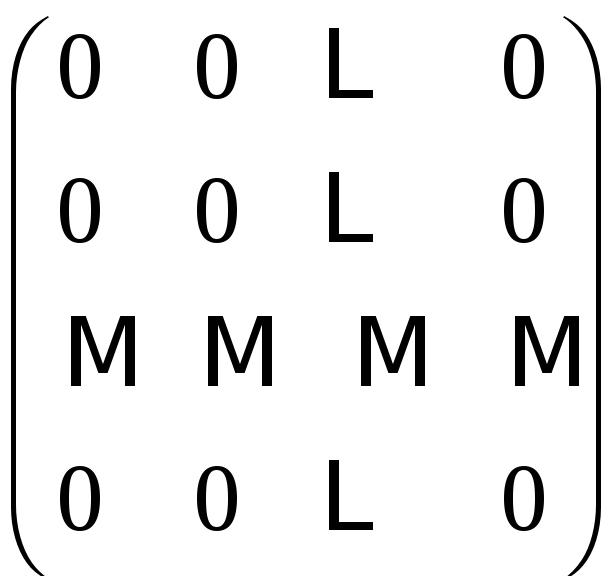
Квадратная матрица такая, что , где 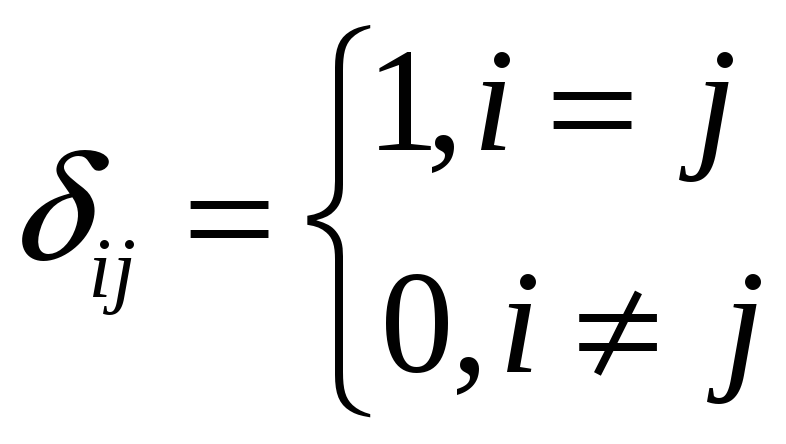называется единичной матрицей порядка .

Определение 9

Элементы матрицы называются главной диагональю матрицы.

Введем операцию сложения матриц и умножения матрицы на число.

Определение 10

Произведением матрицы на число называется матрица такая, что .

Определение 11

Суммой матриц и называется матрица такая, что .

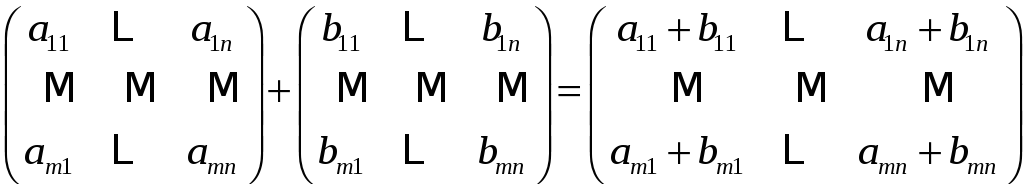
Свойства введенных операций

Для любых матриц , чисел выполняются следующие свойства:

1) . 2) . 3) Существует матрица, обозначаемая такая, что . 4) Существует матрица , обозначаемая такая, что . 5) . 6) . 7) . 8) .

Доказательство

Обозначим через , т.е . Тогда . Так как для чисел коммутативность известна, то . Значит . Аналогично доказываются остальные свойства (пользуемся аналогичными свойствами для чисел). Нулевой матрицей является матрица состоящая из одних нулей

Для матрицы

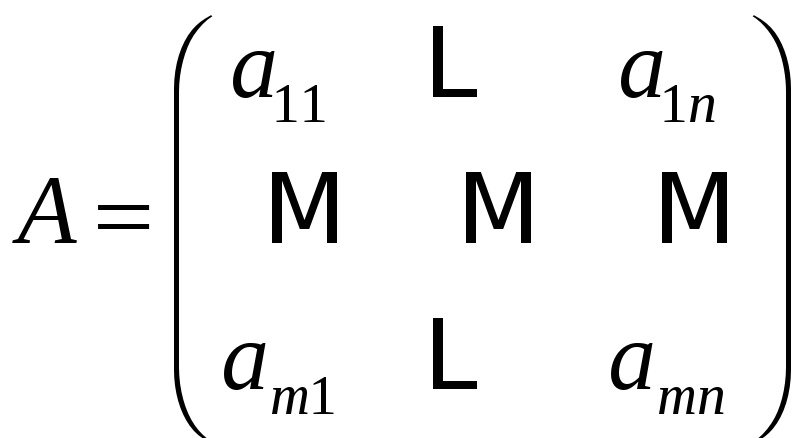
Замечание

Таким образом матрицы размерностью образуют линейно-векторное пространство.

Произведение матриц

Определение 12

Произведением матриц и называется матрица такая, что .

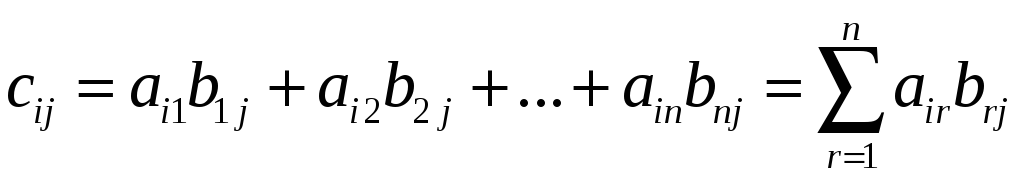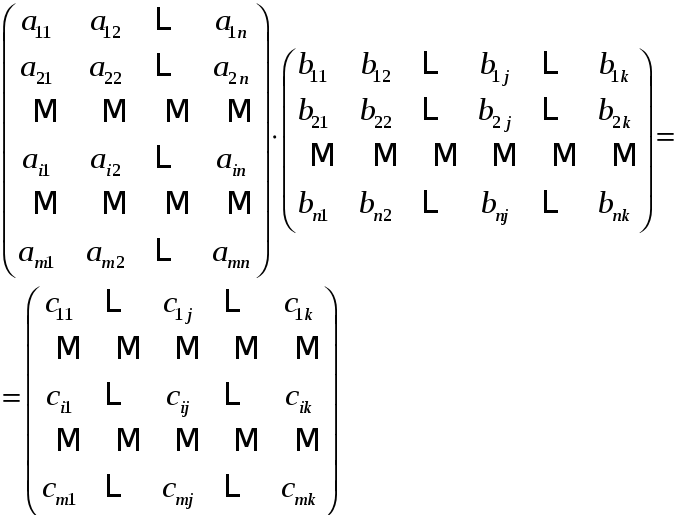
Пример

Пример

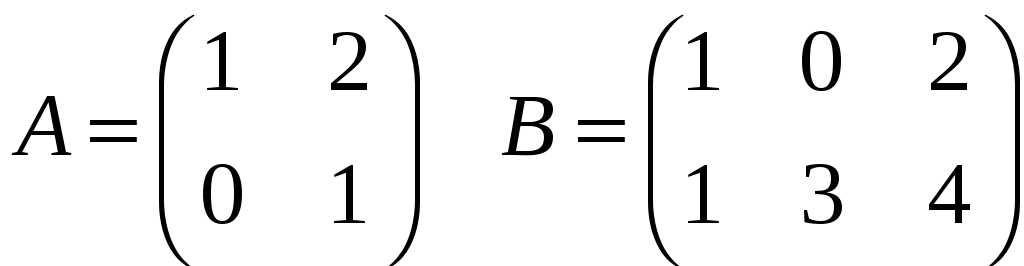. Произведение определено, так как у них размерности , а произведение не определено, так как у них не подходящие размерности ().

Замечание

Для квадратной матрицы размерности и размерности определены оба произведения и .

Замечание

Операция произведения матриц не является коммутативной для матриц, размерности отличной от .

Пример

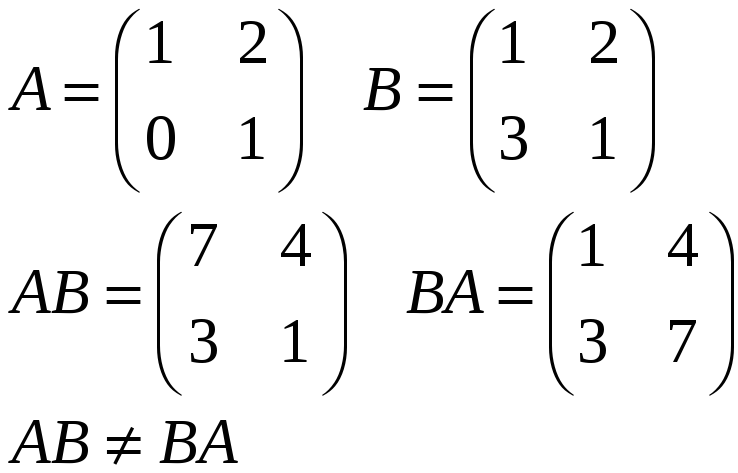
Замечание

Рассмотрим матрицу , нулевую матрицу () и единичную матрицу . является нулевой матрицей . Найдем произведение .

Т.е. . Аналогично можно рассмотреть произведение матрицы и единичной матрицы .

Замечание

Таким образом для квадратной матрицы порядка и единичной матрицы порядка выполняется равенство .

Свойства произведения матриц

Для любых матриц выполняются равенства

1) 2) 3) Для любого числа

Доказательство

Обозначим произведение матриц через . Размерность матрицы . Элемент матрицы находится из равенства 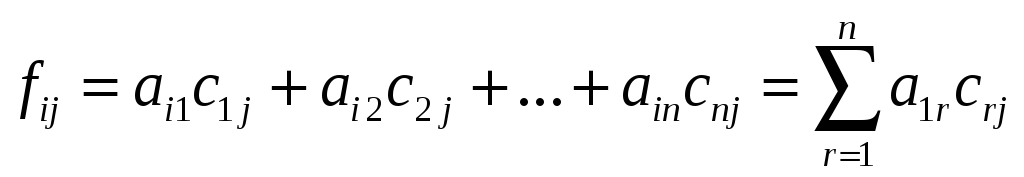. Тогда элемент матрицы размерности

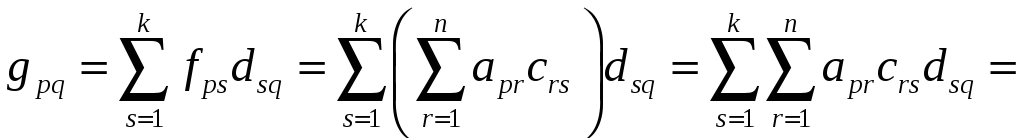
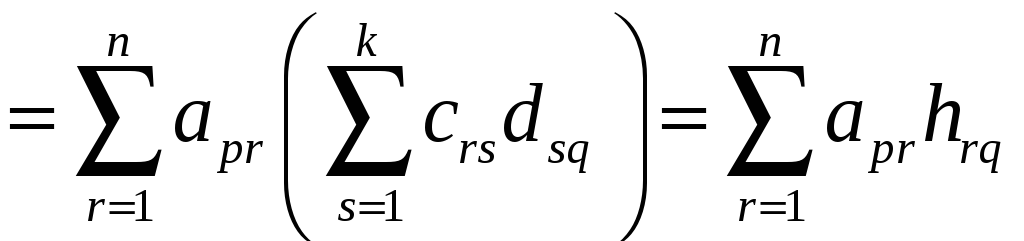, где - элемент матрицы .

Таким образом элемент матрицы равен элементу матрицы .

Аналогично доказываются свойства 2 и 3.

Определение 13

Будем говорить, что матрица 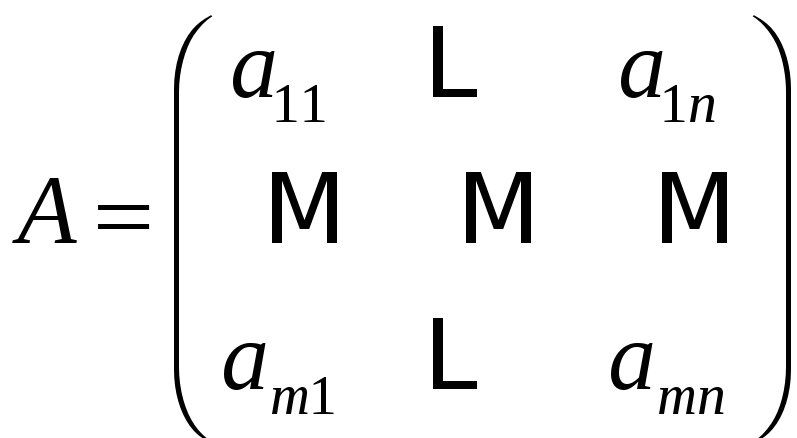разбита на блоки, если она представима в виде 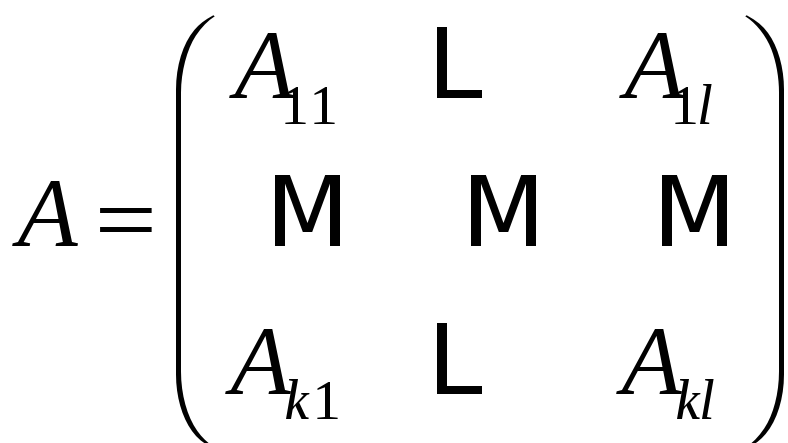, где - матрица размерности , причем 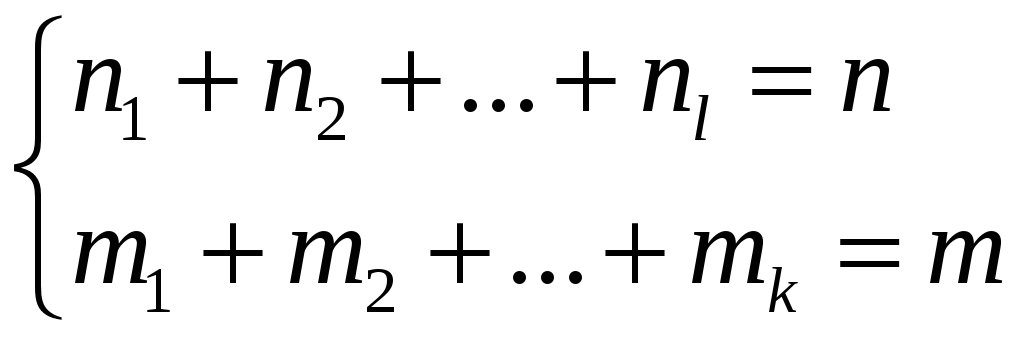. Матрицы называются блоками матрицы .

Сложение блочных матриц

Пусть матрица и матрица разбиты на одинаковые блоки . Тогда для любых чисел и :

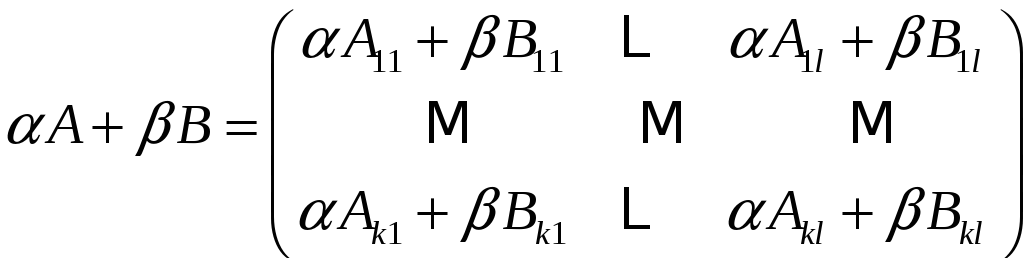
Доказательство

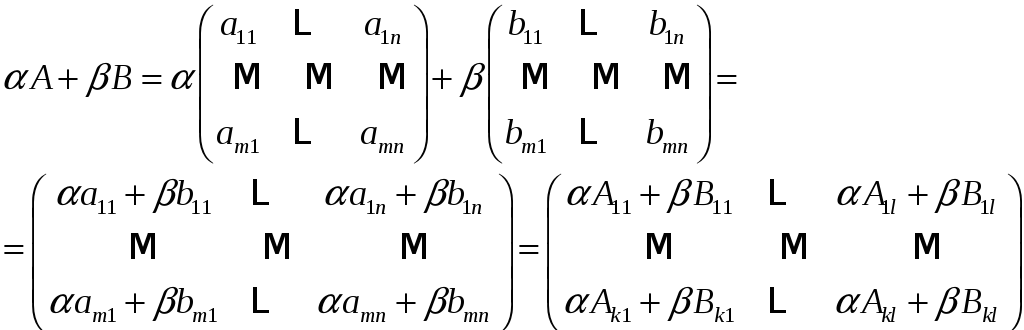
Таким образом сложение и умножение блочных матриц на число аналогично операциям с обычными матрицами.

Умножение блочных матриц

Пусть матрица и матрица разбиты на блоки , т.е. количество блоков в строчке матрицы такое же, как количество блоков в столбце матрицы . При этом размерности матриц и таковы, что определено произведение . Тогда произведение матриц 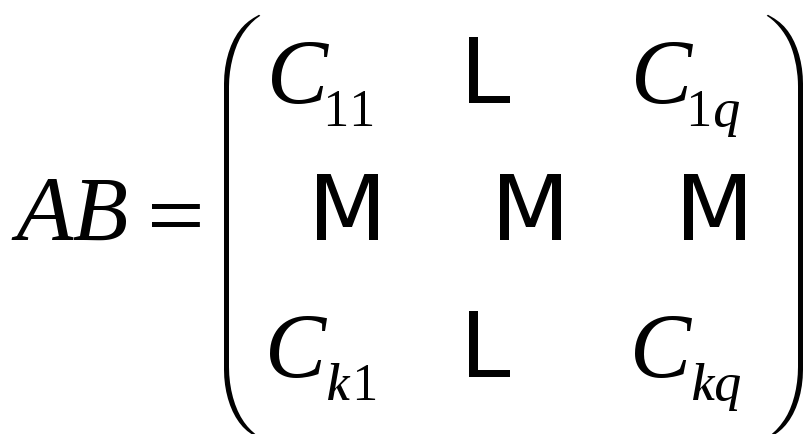, где .

Доказательство

Докажем, что в матрице элемент, стоящий на пересечении первых строк и столбцов образует матрицу , где - количество строк в , а - количество столбцов в . Размерность матрицы равна . Пусть , . Тогда элемент произведения записывается по формуле

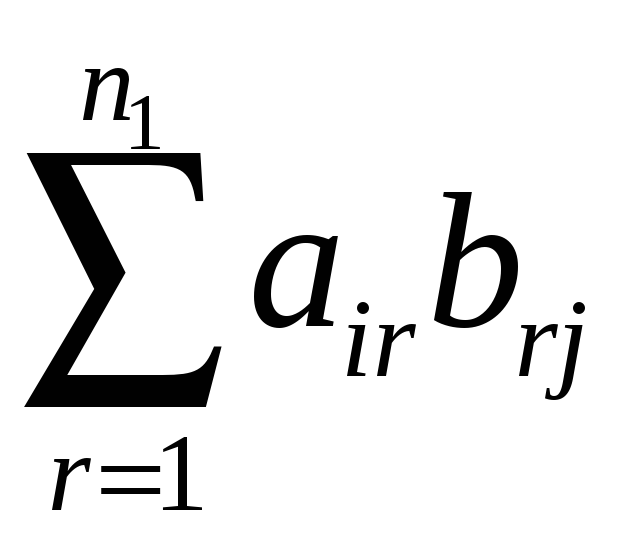является -тым элементом матрицы , 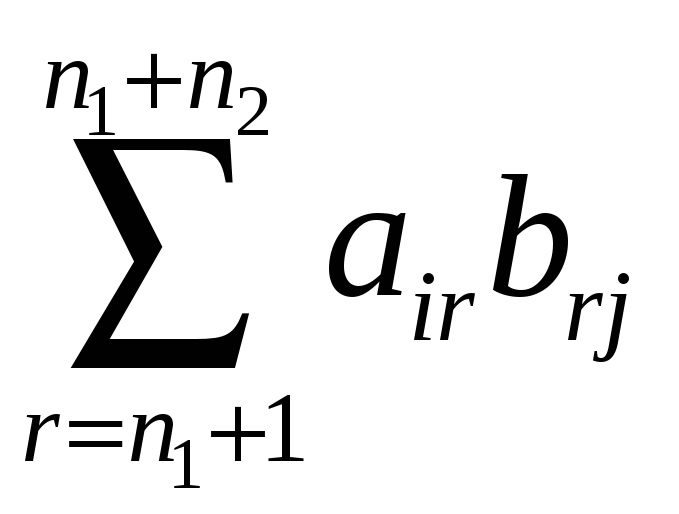является -тым элементом матрицы и т.д. Таким образом получили, что является -тым элементом матрицы . Значит в матрице элемент, стоящий на пересечении первых строк и столбцов образует матрицу . Аналогично доказывается для остальных блоков.

Замечание

Таким образом перемножение матриц, состоящих из блоков аналогично перемножению матриц, состоящих из чисел.

Определение 14

Матрица называется транспонированной к матрице , если . Транспонированная матрица обозначается .

Пример

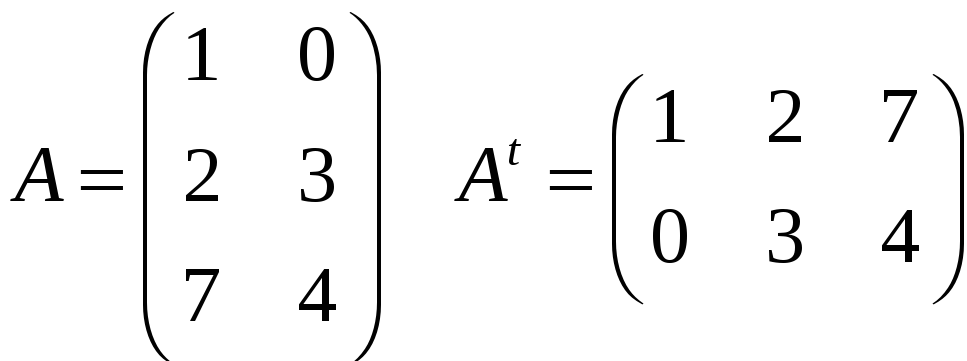
Свойства

1) 2) , - число 3) 4)

Доказательство

Свойства 1, 2, 3 следуют непосредственно из определения.

4)

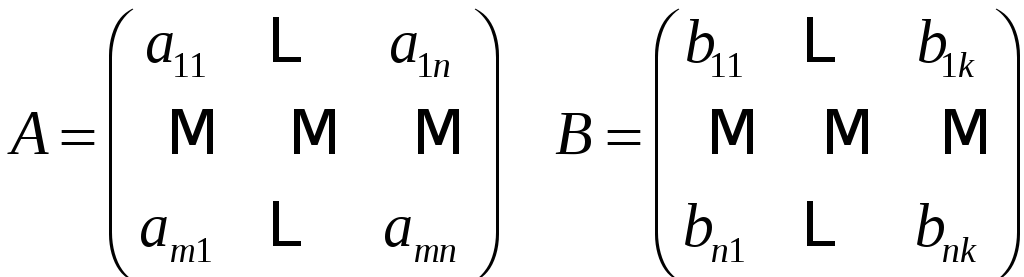
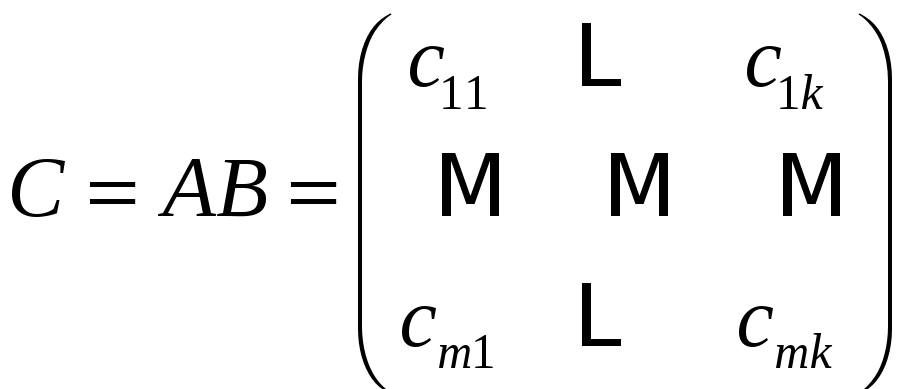
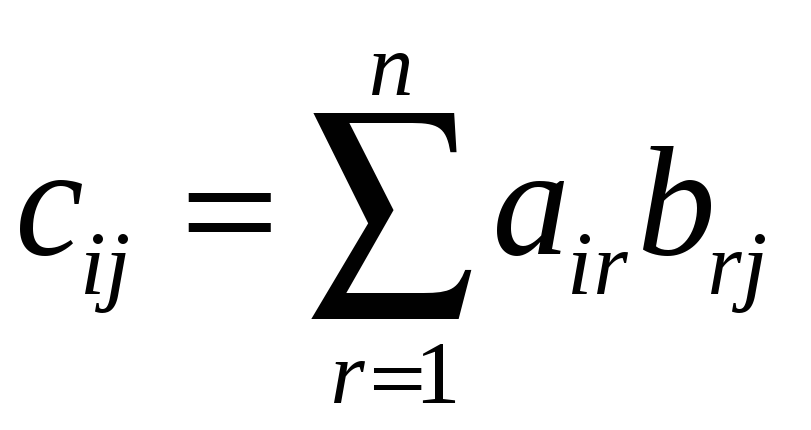
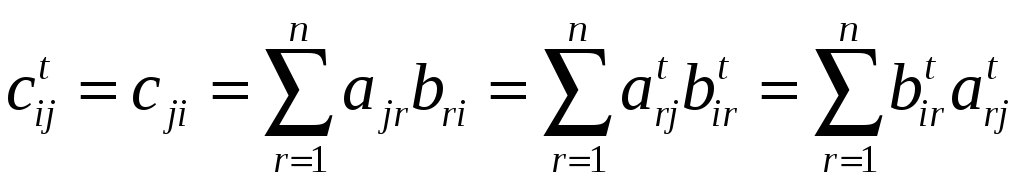
Таким образом равен -тому элементу , т.е. .

Определение 15

Матрица называется симметричной, если .

Пример

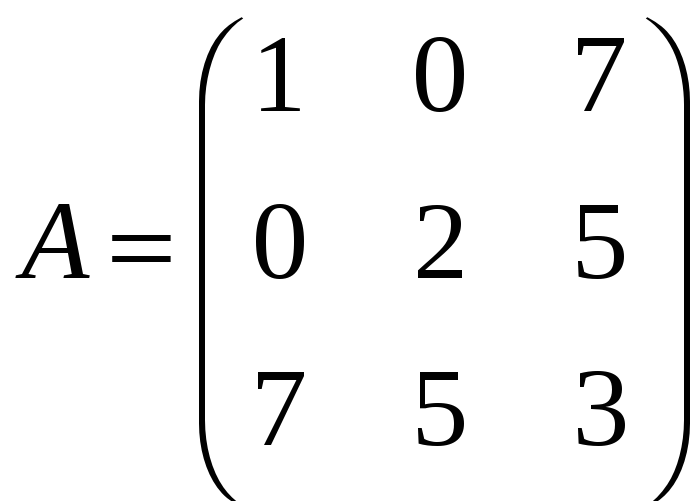
Замечание

Симметричная матрица является квадратной.

Определение 16

Матрица называется кососимметричной, если ().

Пример

Замечание

Кососимметричная матрица является квадратной.

Замечание

У кососимметричной матрицы на главной диагонали стоят нули.

Определение 17

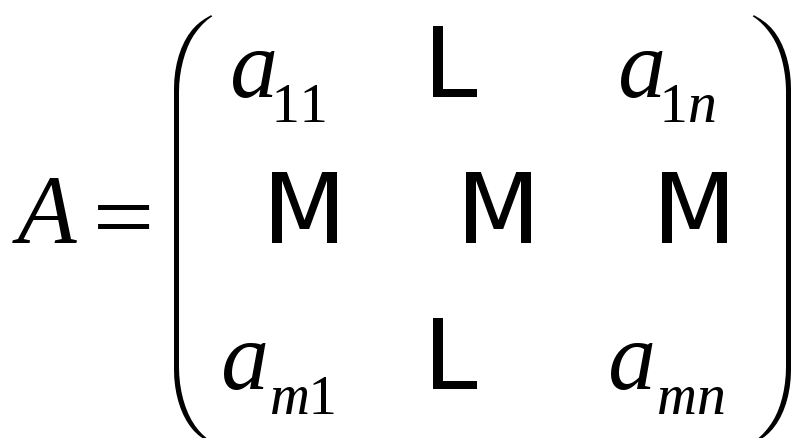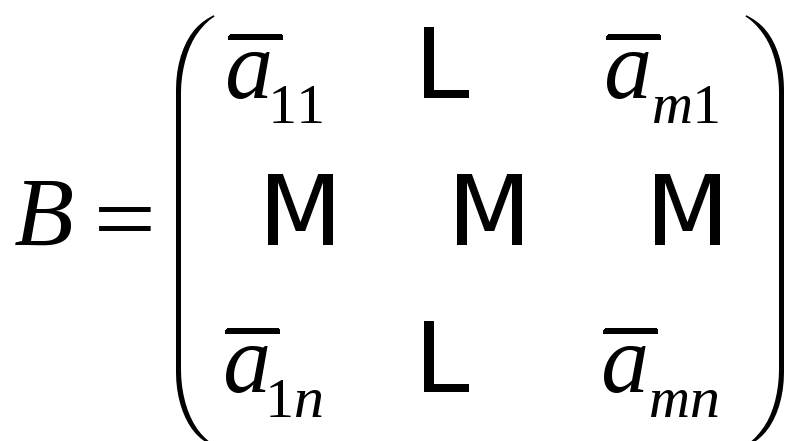Пусть элементы матрицы являются комплексными числами . Тогда матрица называется сопряженной к матрице . Таким образом . Сопряженная матрица обозначается .

Пример

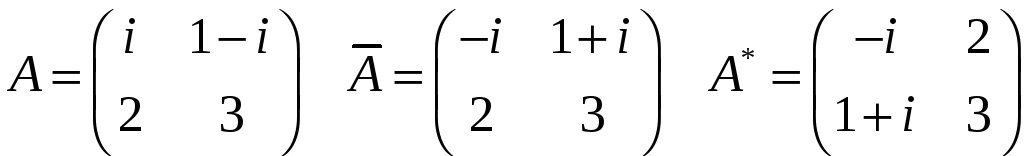
Свойства сопряженной матрицы

1) 2) , - число 3) 4)

Определители

Определение 18

Перестановкой длины называется упорядоченный набор из чисел от до без повторений.

Пример

- перестановка длины - перестановка длины - не является перестановкой - не является перестановкой

Замечание

Количество перестановок длины равно .

Множество всех перестановок длины будем обозначать .

Определение 19

Перестановка называется основной перестановкой длины .

Определение 20

Транспозицией перестановки называется взаимная перестановка двух элементов между собой .

Пример

Определение 21

Говорят, что элементы и , в перестановке образуют инверсию (нарушают порядок), если .

Пример

Элементы 1 и 3 образуют порядок. Элементы 1 и 4 образуют порядок. Элементы 1 и 5 образуют порядок. Элементы 1 и 2 образуют порядок. Элементы 3 и 4 образуют порядок. Элементы 3 и 5 образуют порядок. Элементы 3 и 2 образуют инверсию. Элементы 4 и 5 образуют порядок. Элементы 4 и 2 образуют инверсию. Элементы 5 и 2 образуют инверсию.