Определение 22

Количество инверсий в перестановке будем обозначать . Если является четным числом, то говорят, что перестановка четная. Если является нечетным числом, то говорят, что перестановка нечетная.

Пример

- нечетная перестановка.

Теорема 1

При транспозиции перестановки четность перестановки меняется.

Доказательство

1) Рассмотрим транспозицию соседних элементов . Если элементы и , , образовывали порядок, то и после транспозиции они образуют порядок. Если они образовывали инверсию, то и после транспозиции они образуют инверсию. Аналогично для и , , для и , , для и , . При транспозиции и , если они образовывали порядок, то после транспозиции они образуют инверсию и наоборот. Таким образом количество инверсий при такой транспозиции меняется на 1.

2) Транспозиция произвольных и . Рассмотрим последовательно транспозиции соседних элементов. Мы сделали транспозиций соседних элементов (нечетное число), значит перестановка поменяет четность.

Замечание

Аналогично перестановкам чисел можно рассматривать перестановки , и др. Все рассуждения для перестановок сохраняются.

Определители

Определение 23

Определителем матрицы 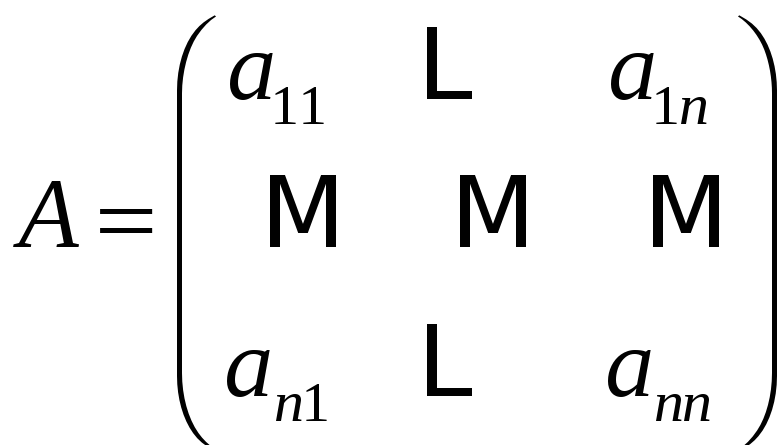называется 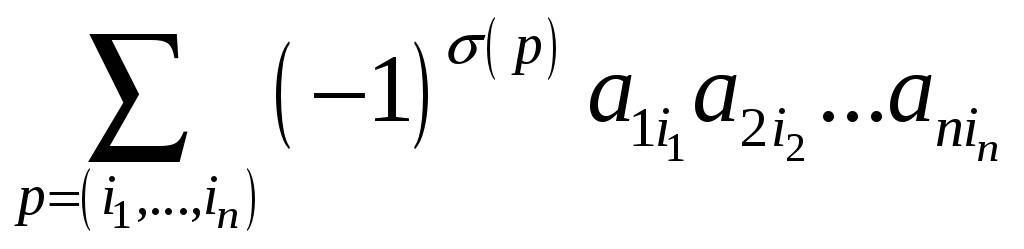, где сумма берется по всем перестановкам длины . Определитель матрицы обозначается , ,

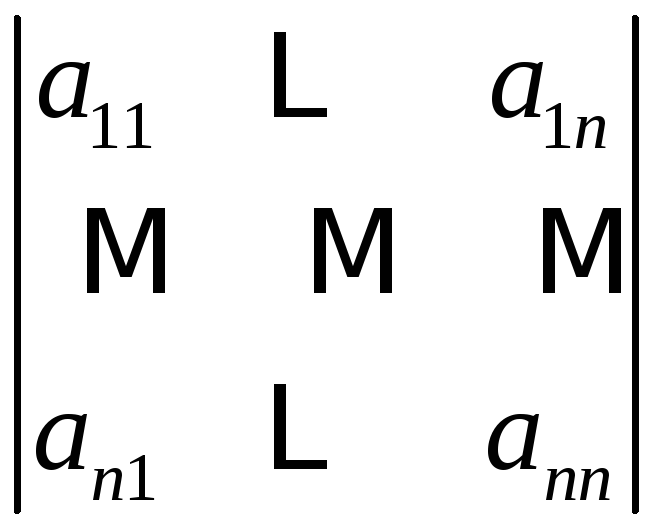
Пример

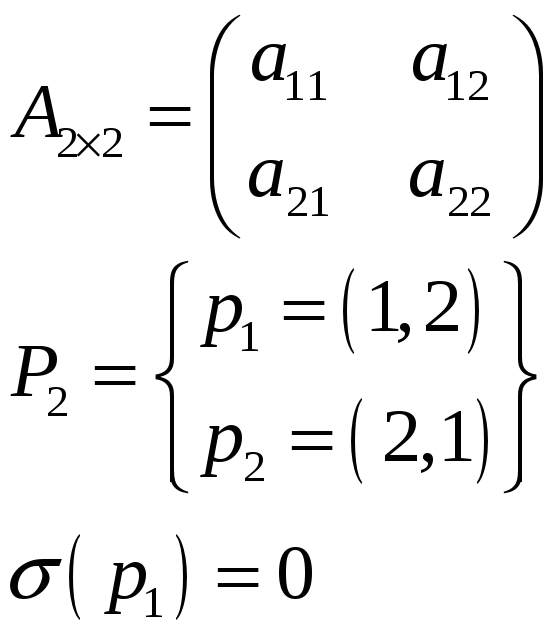
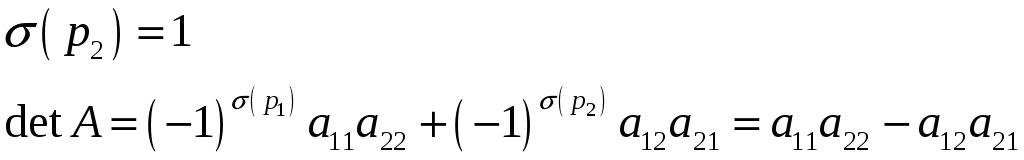
Пример

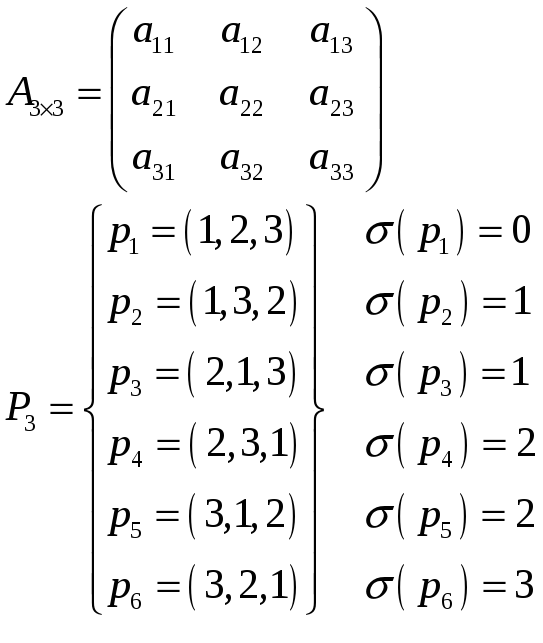
Замечание

Легко видеть, что каждое слагаемое в формуле определителя содержит по одному элементу из каждой строки и по одному элементу из каждого столбца.

Пусть матрица 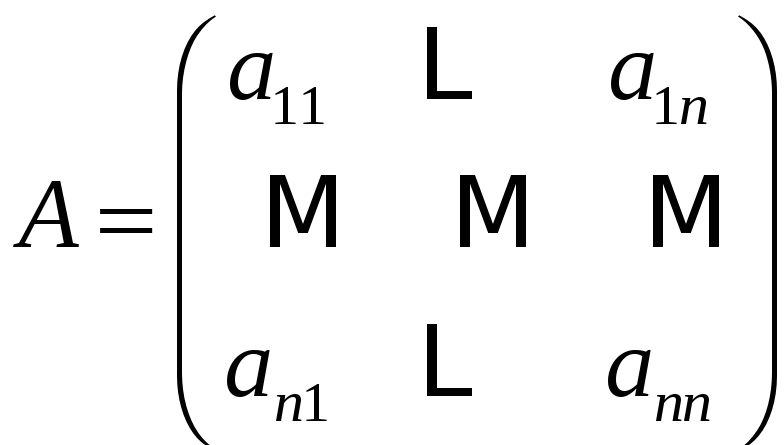. Выясним с каким знаком в определитель входит слагаемое , где и - перестановки длины . Для этого посмотрим, что происходит с перестановками и при транспозиции двух сомножителей этого произведения . Поменяем местами и в указанном произведении. При этом перестановка перейдет в перестановку и будет иметь другую четность относительно исходной перестановки. Аналогично для перестановки . Таким образом, если сумма была четной, то она останется четной после транспозиции, если она была нечетной, то останется нечетной. Т.е. четность указанной суммы сохраняется. Переупорядочим произведение так, чтобы первые индексы образовывали основную перестановку . Получим . Из предыдущих выкладок имеем и имеют одинаковую четность. Значит знак при слагаемом равен .

Рассмотрим 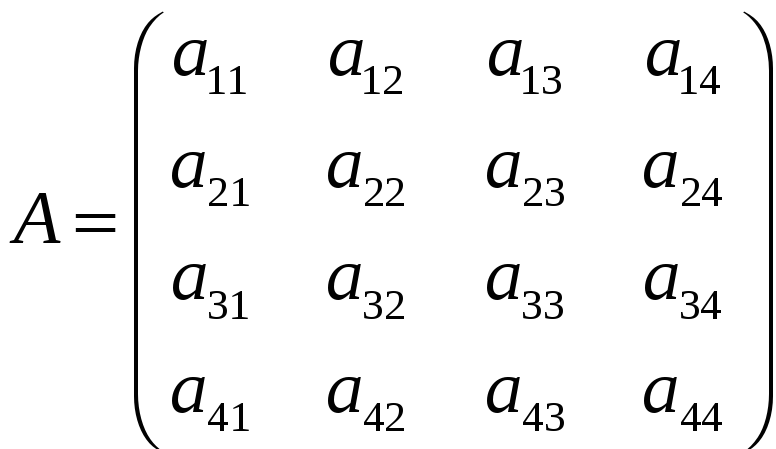. Слагаемое входит в определитель со знаком

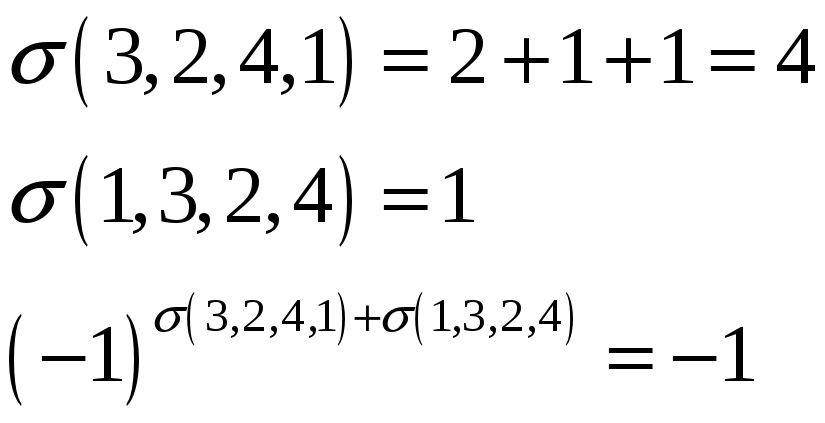
Свойства определителей

1) Матрица называется диагональной, если при .

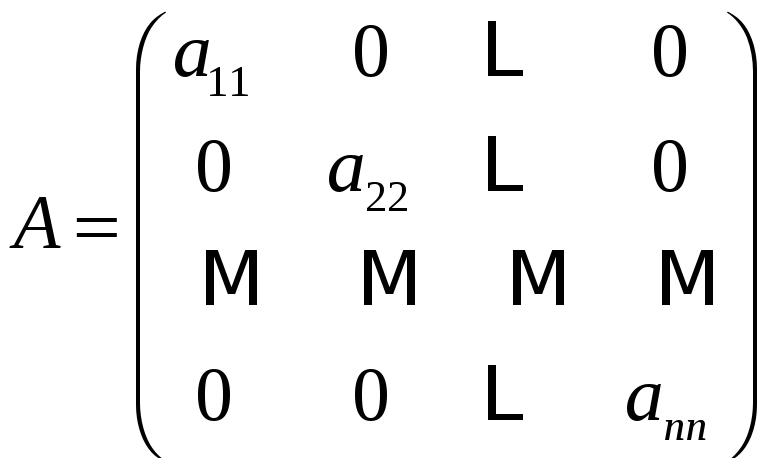
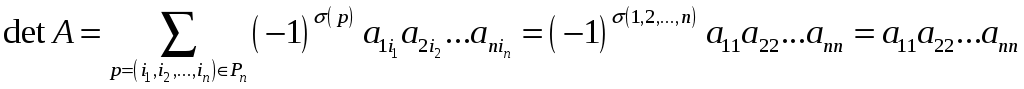2) Пусть 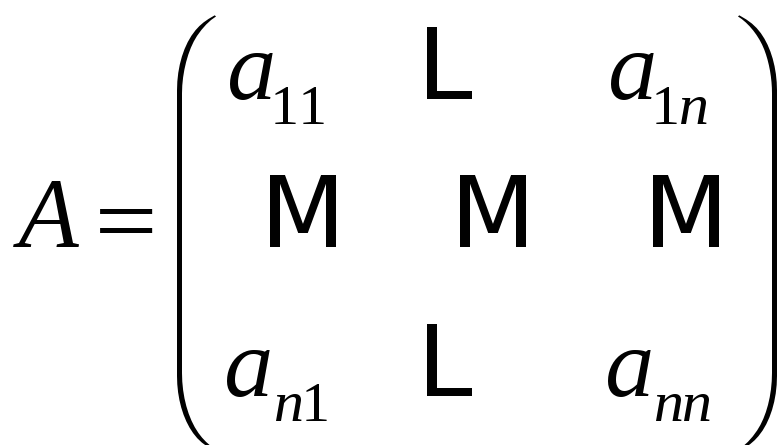, тогда ,

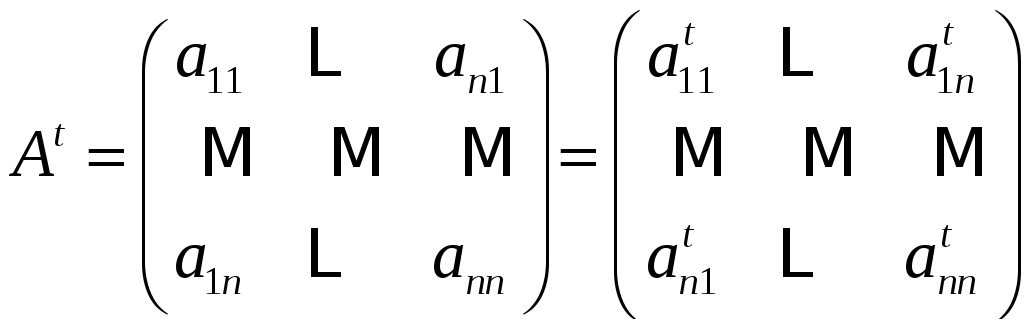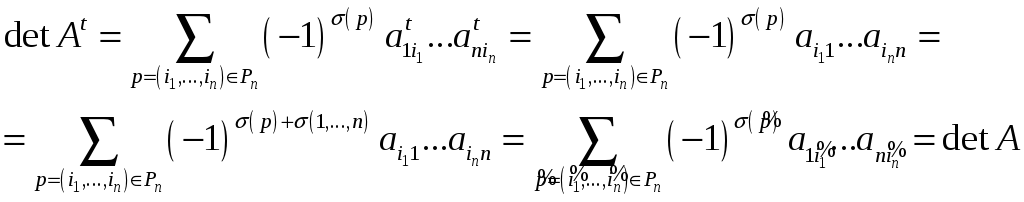
где перестановка получается из перестановки при упорядочивании первых индексов

Замечание

Определение определителя можно было давать не «по строкам» 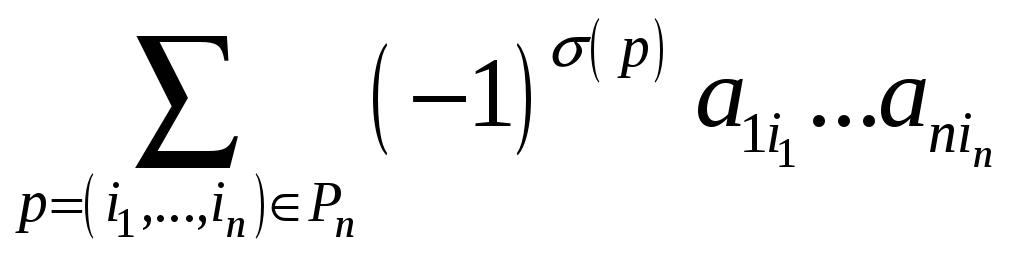, а «по столбцам», т.е. как сумму

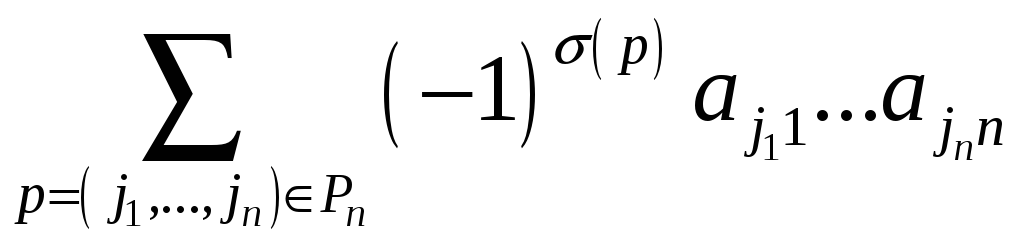
3) Матрица называется верхнетреугольной, если при

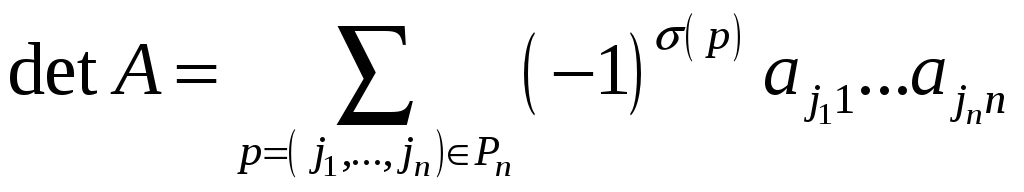. Если , то и соответствующее слагаемое равно . Поэтому остаются слагаемые, где в перестановках . Если , то и соответствующее слагаемое равно . Так как , то остаются слагаемые, где в перестановках . Аналогично для остальных элементов. Значит .

4) Рассмотрим матрицу

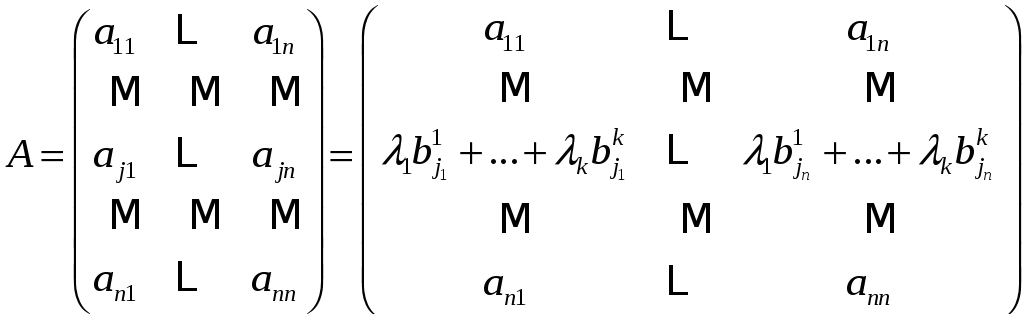, где

Пусть

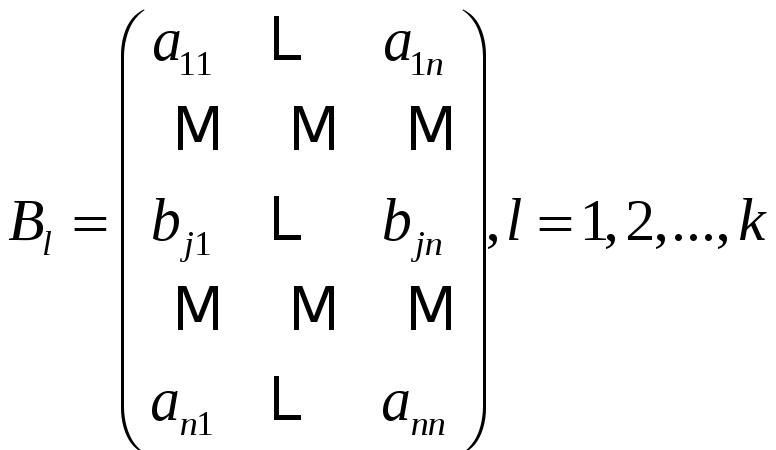
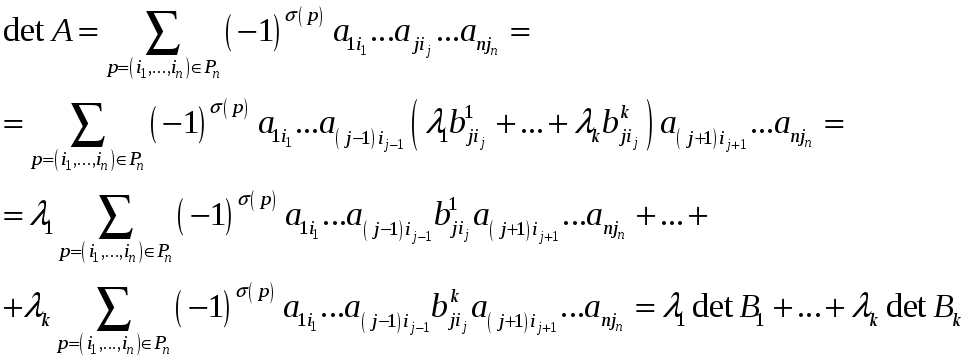
Следствие

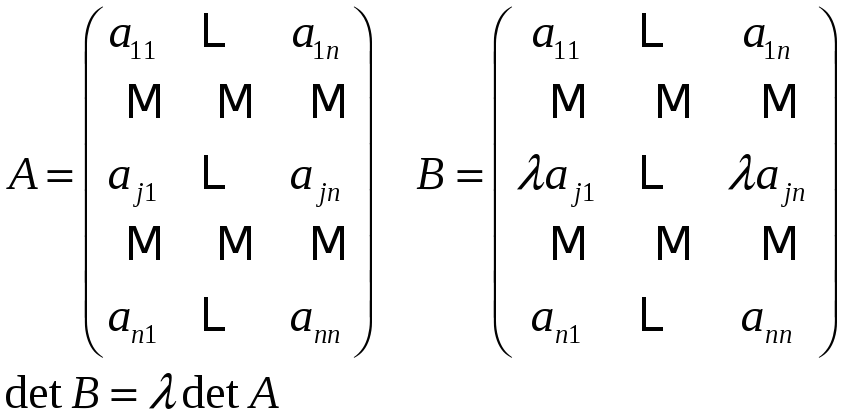
5)

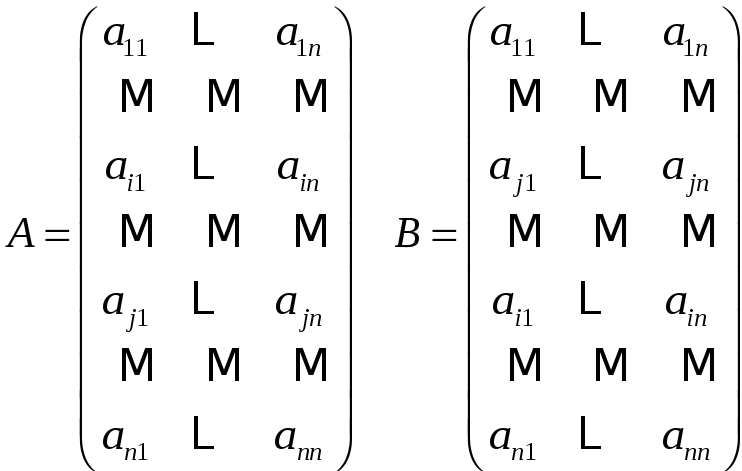
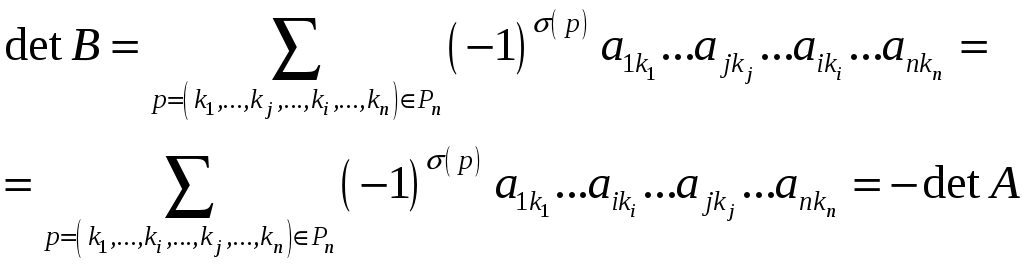
Следствие

Если в квадратной матрице для строк и выполняется , то . Так как -ая и -ая строки совпадают, то после перестановки -ой и -ой строки матрица не изменится .

Следствие

Если к -той строке в матрице 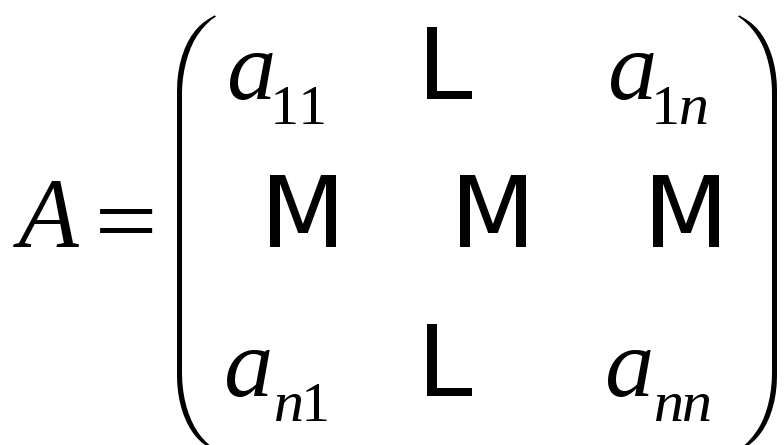добавить -тую строку (), домноженную на некоторое число , то определитель полученной матрицы 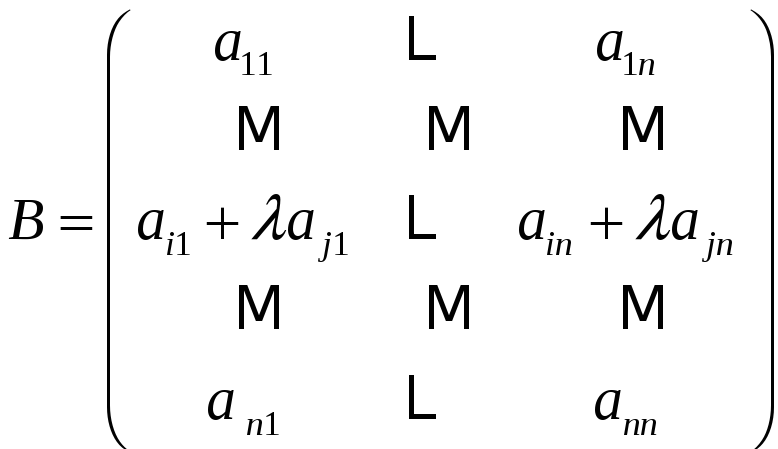будет равен определителю матрицы .

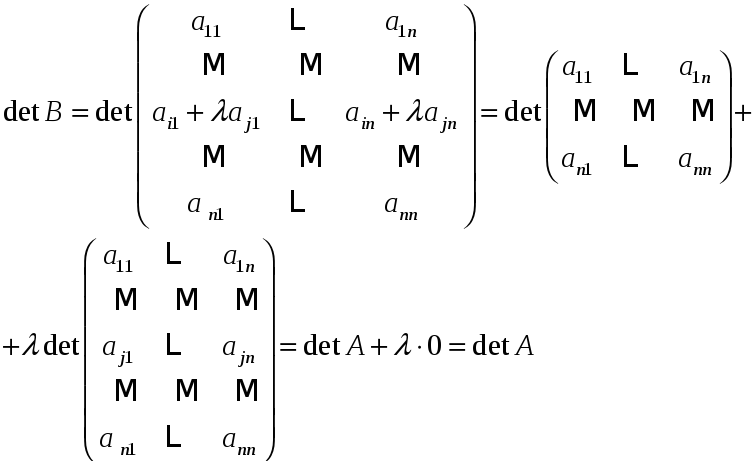
Будем говорить, что строка является линейной комбинацией строк

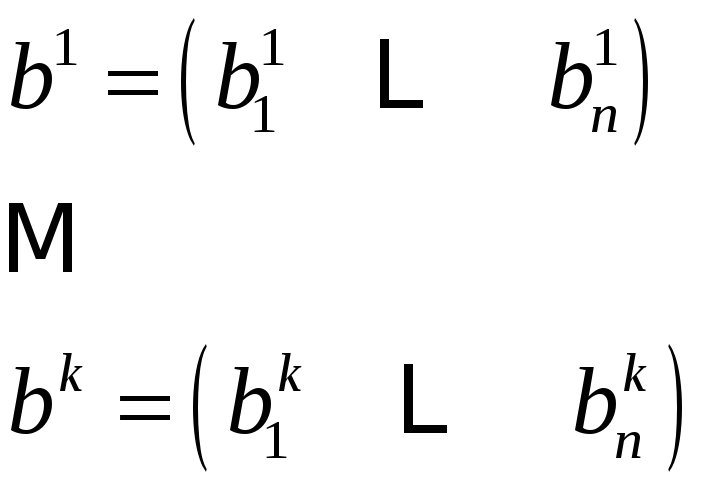
если такие, что

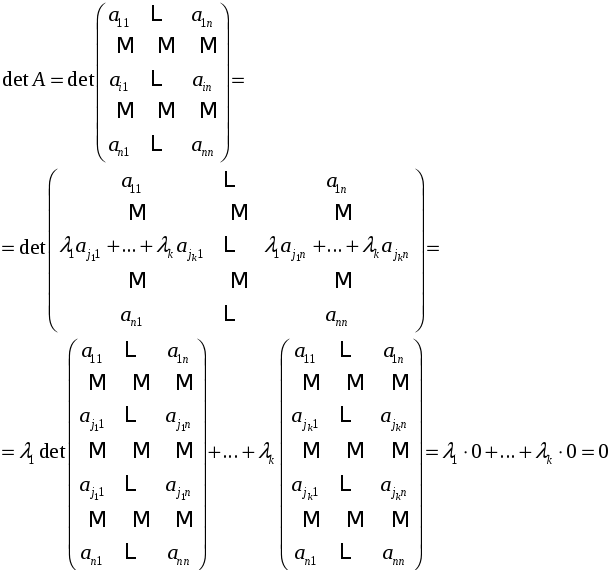
Следствие

Если -ая строка матрицы 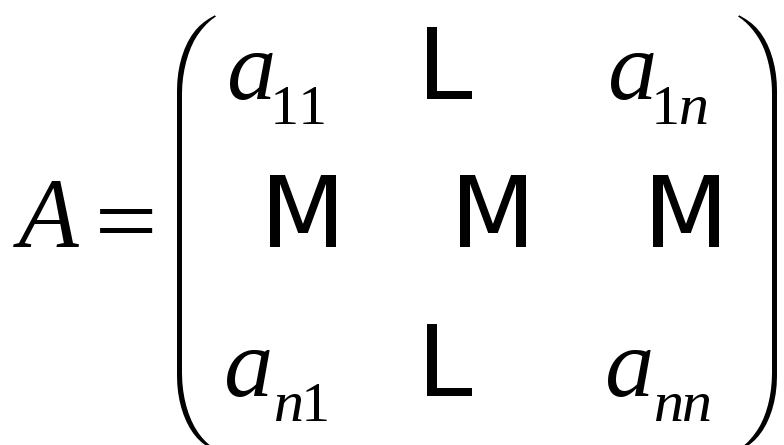является линейной комбинацией строк , , то .

Аналогичные утверждения, сделанные для строк можно сделать для столбцов.