Геометрия и алгебра. Аналитическая геометрия

В течение курса будем рассматривать плоскость и пространство с аксиомами Евклида.

Определение 1

Закрепленным вектором называют отрезок с выбранным одним из двух направлений (от к или от к ). Соответственно вектор с началом в и концом в будем обозначать , а вектор с началом в и концом в через .

Можем дать определение другими словами:

Закрепленным вектором называется упорядоченная пара точек.

Определение 2

Закрепленный вектор, у которого начало и конец совпадает, будем называть нулевым.

Определение 3

Два ненулевых закрепленных вектора, не лежащих на одной прямой будем называть равными, если при соединении отрезком их начал и соединении отрезком их концов образуется параллелограмм.

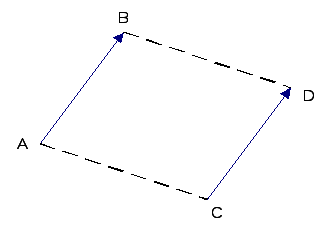
Два ненулевых вектора, лежащих на одной прямой, будем называть равными, если существует третий вектор, не лежащий с ними на одной прямой и равный обоим.

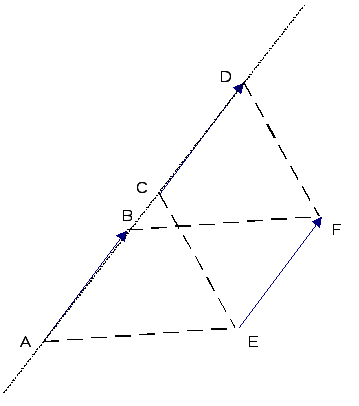
Все нулевые вектора считаем равными.

Теорема 1

Отношение равенства закрепленных векторов обладает следующими свойствами:

1) рефлективность: закрепленный вектор равен сам себе ();

2) симметричность: если вектор равен вектору , то вектор равен вектору ();

3) транзитивность: если вектор равен вектору , а вектор равен вектору , то вектор равен вектору .

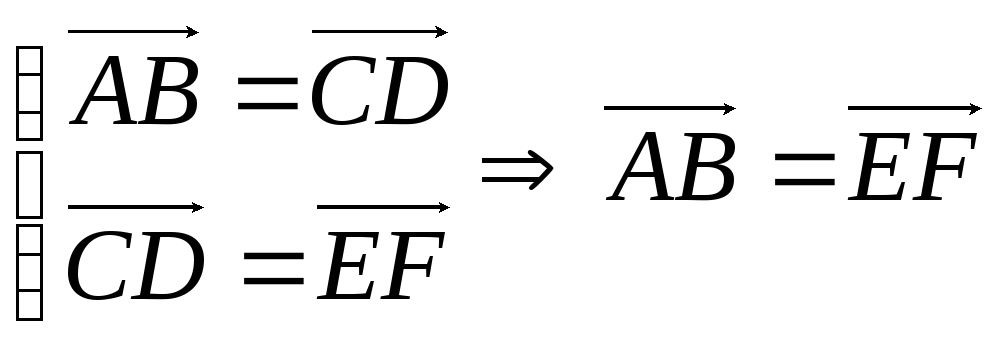Доказательство

1) Если нулевой, то по определению . Если ненулевой, то проведем прямую параллельно вектору и две параллельные прямые через начало и конец вектора , пересекающие первую прямую в точках и .

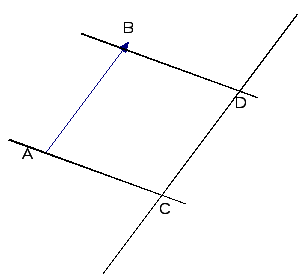
Фигура является параллелограммом. Поэтому . Имеем два вектора и лежат на одной прямой и , значит по определению .

2) По определению.

3)

а) (Векторы , и не лежат в одной плоскости (некомпланарны))

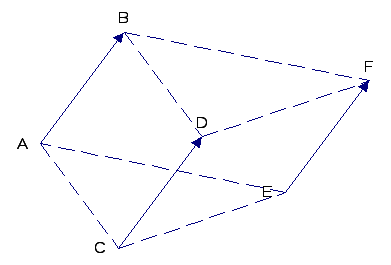
Так как , то . Так как , то . Значит плоскости и параллельны. Так как и , то точки , , , лежат в одной плоскости. Поэтому , т.е. .

б) (Векторы , и лежат в одной плоскости, но никакие два не лежат на одной прямой).

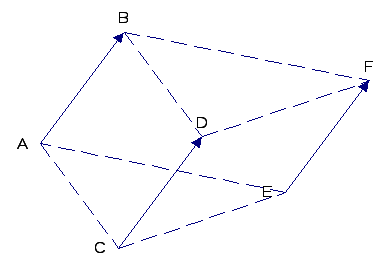
Так как , то . Так как , то . Значит и . Поэтому , т.е. .

в) (Векторы , и лежат в одной плоскости, два из которых лежат на одной прямой).

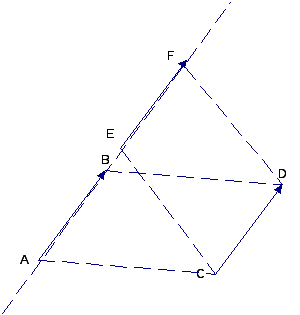
По определению.

г) (Все векторы , и лежат на одной прямой).

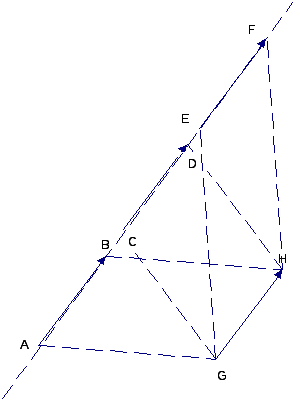
Пусть вектор не лежит на одной прямой с остальными и . Тогда

Так как , то , Так как , то . Отсюда .

Замечание

Отношения, обладающие свойством рефлективности, симметричности и транзитивности обычно называют отношениями эквивалентности.

Определение 4

Классом равенства вектора будем называть множество всех векторов, равных .

Теорема 2

Классы равенства векторов либо не пересекаются, либо совпадают.

Доказательство

Пусть два класса равенства и имеют общий вектор . Тогда для каждого вектора из и вектора из имеем:

(так как ) (так как )

Поэтому и и по свойству транзитивности . Аналогично . Получаем, что . Таким образом, и , то есть любой элемент из входит в и наоборот.

Следствие

Множество всех закрепленных векторов распадается на попарно непересекающиеся классы векторов.

Определение 5

Свободными векторам будем называть классы равенства закрепленных векторов. Свободные вектора будем обозначать , или , .

Определение 6

Будем говорить, что свободные векторы равны, если их классы совпадают. При этом писать будем . Класс нулевых закрепленных векторов будем обозначать или . Вместо записи будем писать .

Линейные операции над векторами

Под линейными операциями над векторами будем понимать сложение векторов и умножение векторов на действительные числа.

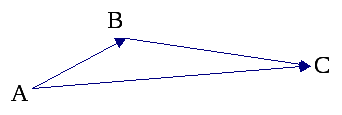
Определение 7

Суммой закрепленных векторов и называется вектор .

Определение 8

Произведением вектора на действительное число называется вектор такой, что .

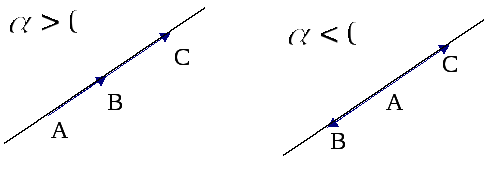
Векторы и лежат на одной прямой и в случае точки и лежат на прямой по одну сторону от , а в случае – по разные.

Определение 9

Суммой свободных векторов и называется свободный вектор (класс равенства), порожденный суммой закрепленных векторов и .

Определение 10

Произведением свободного вектора на число называется свободный вектор , порожденный вектором , где .

Теорема 3

Определение суммы свободных векторов и произведения свободного вектора на число корректна, то есть сумма не зависит от выбора закрепленных векторов, и произведение не зависит от выбора закрепленного вектора.

Доказательство

Докажем частично корректность суммы.

Нам надо показать, что выбор пары , и другой пары , порождают один и тот же свободный вектор (класс равенства).

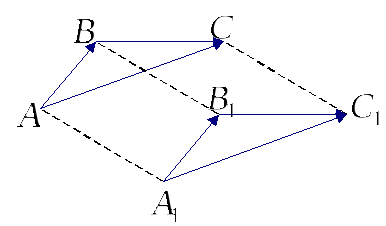
Пусть , и , не лежат в одной плоскости. Тогда (см. доказательство теоремы 1). Значит векторы и порождают один и тот же свободный вектор (класс равенства).

Определение 11

Свободные векторы и будем называть коллинеарными, если закрепленные векторы и коллинеарны.

Теорема 4

Если векторы и коллинеарны, то найдется число такое, что либо , либо .

Доказательство

Рассмотрим и . Так как и , то возьмём , где берется знак «», если и лежат по одну сторону от точки , и «–» если по разные. Тогда и векторы и порождают одинаковые классы равенства. Значит .

Определение 12

Будем говорить, что на множестве задана операция сложения, если каждой упорядоченной паре из поставлен в соответствие элемент из .

Определение 13

Будем говорить, что на множестве задана операция умножения на действительное число, если каждой паре число и элемент из поставлен в соответствие элемент из .

Определение 14

Множество будем называть линейно-векторным пространством, если на нем определены операции сложения, умножения на число, которые удовлетворяют свойствам:

1) для любых и из верно равенство ;

2) для любых , и из верно равенство ;

3) существует элемент , который называет нулевым и обозначают , который обладает следующим свойством: для каждого ;

4) Для каждого элемента существует элемент такой, что . Этот элемент называется обратным элементом к и обозначается .

5) Для любого числа и любых и выполняется .

6) Для любых чисел и и любого выполняется .

7) Для любых чисел и и любого выполняется .

8) Для любого элемента .