10. Дифференциал, его геометрический смысл, вычисление дифференциала сложной функции.

Ответ:

Дифференциал функции y = f(x) равен произведению её производной на приращение независимой переменной x (аргумента) и обозначается dy.

Вычисление дифференциала.

Дифференциалы сложных функций:

11. Наибольшее и наименьшее значения функции на отрезке.

Ответ:

Пусть функция y = f(x),x[a; b], непрерывна на отрезке [а; b], дифференцируема во всех точках этого отрезка и имеет на нем конечное число критических точек первого рода.

Очевидно, что если данная функция монотонна на отрезке [а; b], то наибольшее и наименьшие значения достигаются на концах этого отрезка, а именно:

1) если функция f(x) возрастающая, то f(а)-наименьшее значение и f(b)—наибольшее значение;

2) если функция f(x) убывающая, то f(a)—наиболь­шее значение и f(b)— наименьшее значение.

Если функция f(x) не является монотонной, то свое наибольшее значение на отрезке [а;b] она дости­гает либо в одной из то­чек максимума, либо на одном из концов этого отрезка. Точно так же наименьшее значение  на отрезке [а; b] функция f(x) достигает либо в одной из точек минимума, либо на одном из концов отрезка [а; b].

Чтобы найти наибольшее и наимень­шее значения функции нужно:

1) найти критические точки первого рода данной функции;

2) вычислить значения функции во всех критических точках, принадлежащих интервалу [а;b] и на концах отрезка [a; b];

3) из полученных значений выбрать наибольшее и наименьшее.

12. Определение и геометрический смысл определенного интеграла. Формула Ньютона – Лейбница для вычисления площади криволинейной трапеции.

Ответ:

Если существует конечный

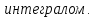
Геометрический смысл определенного интеграла.

Определенный интеграл от а до b функции f(x) равен площади S соответствующей криволинейной трапеции.

Формула Ньютона – Лейбница для вычисления площади криволинейной трапеции.

13. Определение несобственного интеграла и его вычисление.

Ответ:

Определенный интеграл называется несобственным интегралом, если нижний предел интегрирования a или верхний предел b (или оба предела) являются бесконечными, или если функция f(x)имеет точки разрыва на отрезке [a,b].

Если f(x)− непрерывная функция на интервале [a,+∞), то несобственный интеграл выражается через предел в виде:

Если f(x) − непрерывная функция на интервале [a,∞), то несобственный интеграл определяется формулой 

14. Дифференциальные уравнения и их решение.

Ответ:

Дифференциальное ур-е – ур-е, связывающее между собой значение независимой переменной х, неизвестной функций y = f (x) и ее производной.

Порядок ур-е – мах. порядок входящей в него производной.

Решение дифференциального ур-е – функция у(х), которое обращает ур-е в тождество.

ОДУ первого порядка – это ур-е вида: .

Общее ур-е:

Уравнения с разделяющимися переменными:

Уравнения вида:

Можно легко свести к уравнению с разделяющимися переменными:

Интегрируя это уравнения получим:

Уравнения с однородной правой частью:

Это ур-е сводится к уравнению с разделяющимися переменными относительно новой независимой функции u(x) заменой:

Подставляя в ур-е y=xu, y^’=u+xu^’, получим:

где p(x), q(x) – непрерывные функции

Линейные уравнения:

Представим y(x) = u(x)*v(x).

Тогда:

и ур-е приводится к виду:

Сначала находим функцию:

Затем: