
- •§ 16. Елементи теорії функцій комплексної змінної
- •16.1 Функції комплексної змінної.
- •16.1.1. Основні поняття
- •16.1.2 Границя і неперервність функції комплексної змінної
- •16.1.3. Основні елементарні функції комплексної змінної
- •16.1.3.1. Показникова функція
- •16.1.3.2. Логарифмічна функція
- •16.1.3.5. Тригонометричні функції
- •16.1.3.6. Гіперболічні функції
- •16.1.3.7. Обернені тригонометричні і гіперболічні функції
- •16.1.4. Диференціювання функції комплекснї змінної. Умови Ейлера-Даламбера.
- •16.1.5. Аналітична функція. Диференціал
- •16.1.6. Геометричний зміст модуля і аргумента похідної. Поняття про конформне відображення
- •Приклади конформних відображень, що здійснюються деякими елементарними функціями див. Додаток 1.
- •16.2. Інтегрування функції комплексної змінної
- •16.2.1 Означення, властивості і правила обчислення інтеграла
- •16.2.2. Теорема Коші. Первісна , невизначений інтеграл. Формула Ньютона-Лейбніца.
- •16.2.3. Інтеграл Коші. Інтегральна формула Коші
- •16.3. Ряди в комплексній площині
- •16.3.1. Числові ряди
- •16.3.2. Степеневі ряди
- •Ряд Тейлора
- •Нулі аналітичної функції
- •Ряд Лорана
- •Ряд Лорана для функції
- •○ Скористаємося відомим розкладом
- •16.3.6. Класифікація особливих точок. Зв'язок між нулем і полюсом функції
- •Усувні особливі точки
- •Істотно особлива точка
- •16.4. Лишок функції
- •16.4.1. Поняття лишка і основна теорема про лишки
- •16.4.2. Обчислення лишків. Застосування лишків в обчисленні інтегралів
16.1.3.5. Тригонометричні функції
Тригонометричні
функції комплексного аргументу
 визначаються рівностями
визначаються рівностями
 ,
,
 ,
,
 ,
,
 .
.
При
дійсних
 ці означення
приводять до тригонометричних функцій
дійсної змінної. Так, при
ці означення
приводять до тригонометричних функцій
дійсної змінної. Так, при
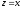 (
( )
)
 .
.
Тригонометричні функції комплексної змінної зберігають багато властивостей тригонометричних функцій дійснї змінної. Зокрема,
 ,
,
 ,
,
 ,
,
 ,
,
 ,
,
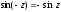 ,
,
 ,
,
 при
при
 (
( ),
),
 ,
,
 ,
,
 ,
,
 і т.д.
Доведемо, наприклад, першу властивість:
і т.д.
Доведемо, наприклад, першу властивість:


 .
.
Відзначимо,
що тригонометричні функції
 та
та
 у комплексній площині
у комплексній площині
 необмежені:
необмежені:
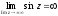 ,
,
 .
Так, наприклад,
.
Так, наприклад,
 ,
,
 .
.
16.1.3.6. Гіперболічні функції
Ці функції визначаються рівностями
 ,
,  ,
,  ,
,  .
.
Легко
замітити зв'язок між гіперболічними і
тригонометричними функціями. Замінюючи
в зазначених функціях
 на
на
 ,
одержимо:
,
одержимо:
 , чи
, чи
 ,
,
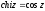 (а
також
(а
також
 ,
,
 ).
).
Користуючись
цими рівностями, можна одержати ряд
формул, що пов'язують гіперболічні
функції. Так, замінюючи у формулі
 тригонометричні функції гіперболічними,
одержимо
тригонометричні функції гіперболічними,
одержимо
 ,
,
або
 .
Тому що тут
.
Тому що тут
 -
будь-яке комплексне число, то
-
будь-яке комплексне число, то
 можна замінити на
можна замінити на
 ;
одержимо
;
одержимо
формулу
 .
.
Наведемо ще ряд формул:
 ,
,
 ,
,
 ,
,  ,
,
 ,
,  ,
,
і т.д.
З
означення
гіперболічних функцій випливає, что
функції
 і
і
 періодичні з періодом
періодичні з періодом
 ;
функції
;
функції
 і
і
 мають період
мають період
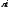 .
.
16.1.3.7. Обернені тригонометричні і гіперболічні функції
Число
 називається арксинусом
числа
називається арксинусом
числа
 ,
якщо
,
якщо
 ,
і позначається
,
і позначається

Використовуючи
означення
синуса, маємо
 ,
або
,
або
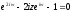 .
Звідси
.
Звідси
 ,
тобто
,
тобто
 (перед коренем можна не писати знак
(перед коренем можна не писати знак
 ,
тому що
,
тому що
 має два значення). Тоді
має два значення). Тоді
 ,
або
,
або
 .
Таким чином,
.
Таким чином,
 .
.
Функція
 багатозначна (нескінченнозначна).
Аналогічно визначаються інші обернені
тригонометричні функції. Можна показати,
що
багатозначна (нескінченнозначна).
Аналогічно визначаються інші обернені
тригонометричні функції. Можна показати,
що
 ,
,

 ,
,

 .
.
Функції,
обернені гіперболічним, позначаються
відповідно
 (ареасинус),
(ареасинус),
 (ареакосинус),
(ареакосинус),
 (ареатангенс),
(ареатангенс),
 (ареакотангенс).
(ареакотангенс).
Обернені гіперболічні функції подаються так:
 ,
,  ,
,
 ,
,  .
.
Усі ці функції нескінченнозначні.
16.1.4. Диференціювання функції комплекснї змінної. Умови Ейлера-Даламбера.
Нехай однозначна функція w=f(z) визначена в деякому околі точки z, включаючи і саму точку. Тоді границя
 ,
(1.4)
,
(1.4)
якщо віна існує, називається похідною функції f(z) у точці z, а функція f(z) називається дифференційовною у точці z.
Підкреслимо,
що в рівності (1.4)
 будь-яким чином прямує до нуля, тобто
точка
будь-яким чином прямує до нуля, тобто
точка
 може наближатися до точки z по кожному
з нескінченної множини напрямків (див.
рис. 2) (в аналогічній ситуації для функції
однієї дійсної змінної точка
може наближатися до точки z по кожному
з нескінченної множини напрямків (див.
рис. 2) (в аналогічній ситуації для функції
однієї дійсної змінної точка
 наближається до точки x
лише
по двох напрямках: ліворуч і праворуч).
наближається до точки x
лише
по двох напрямках: ліворуч і праворуч).
Рис. 2
З
дифференційовності функції f(z)
в деякій точці z
випливає її неперервність у цій точці
(відношення
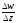 при
при
 може прямувати до скінченної границі
f(z)
лише за умови, що і
може прямувати до скінченної границі
f(z)
лише за умови, що і
 ).
Обернене твердження не має місця.
).
Обернене твердження не має місця.
При яких умовах функція w=f(z) , буде диференційовна в заданій точці?
Теорема 1.1. Якщо функція w=u(x;y)+iv(x;y) визначена в деякому околі точки z=x+iy, причому в цій точці дійсні функції u(x;y) і v(x;y) дифференційовні, то для дифференційовности функції w=f(z) у точці z необхідно і достатньо, щоб у цій точці виконувалися рівності
 ,
,
 (1.5)
(1.5)

Рівності
(1.5)
називаються умовами
Ейлера-Даламбера (або
умовами Коші-Рімана).
□ Необхідність
Нехай
функція f(z)
диференційовна в точці z,
тоді границя (1.4)
існує і не залежить від шляху, по якому
 .
Можна вважати, що точка
.
Можна вважати, що точка
 наближається до точки z
по прямій, паралельній дійсній осі (осі
Ox),
тобто
наближається до точки z
по прямій, паралельній дійсній осі (осі
Ox),
тобто
 (рис. 3).
(рис. 3).
Рис. 3 Тоді




 .
.
Якщо ж
точка
 наближається до точки z
по прямій, паралельній уявній осі (осі
Oy),
то
наближається до точки z
по прямій, паралельній уявній осі (осі
Oy),
то
 В цьому випадку
В цьому випадку

 .
.
Порівнявши
знайдені границі, одержимо
 .
.
Звідси
випливає:
 .
.
Достатність
Нехай тепер умови (1.5) виконуються. Доведемо, что функція f(z) диференційовна.
Так як
функції u(x;y)
і
v(x;y)
диференційовні в точці z=x+iy,
то їхні повні прирости можна подати у
вигляді

 ,
,
 ,
де
,
де
 і
і
 – нескінченно малі більш високого
порядку, ніж
– нескінченно малі більш високого
порядку, ніж
 .
Тоді
.
Тоді


Заміняючи
в чисельнику правої частини
 на
на
 ,
,
 на
на
 ,
відповідно до умов (1.5),
одержуємо:
,
відповідно до умов (1.5),
одержуємо:
 , де
, де
 ,
,
тобто
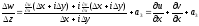 ,
,
а
 – нескінченно мала вищого порядку
відносно
– нескінченно мала вищого порядку
відносно
 .
Звідси випливає, що
.
Звідси випливає, що існує.
При цьому
існує.
При цьому
 .
■
.
■
З урахуванням умов Ейлера-Даламбера (1.5) похідну диференційовної функції f(z) можна знаходити за формулами

 ,
,
 ,
,
 .
(1.6)
.
(1.6)
Правила
диференціювання функцій дійсної змінної
справедливі і для функцій комплексної
змінної, диференційованих в точці z.
Це означає, що якщо
 і
і
 диференційовні в деякій точці z
комплексної площини, то справедливі
такі твердження:
диференційовні в деякій точці z
комплексної площини, то справедливі
такі твердження:
1.

2.
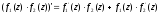
3.
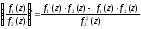

4. Якщо
 диференційована в точці z, а f(w)
диференційована
в точці
диференційована в точці z, а f(w)
диференційована
в точці
 ,
то
,
то
 .
.
5. Якщо
в деякій точці z
функція f(z)
диференційовна й існує функція
 ,
диференційовна в точці w=f(z),
причому
,
диференційовна в точці w=f(z),
причому
 ,
то
,
то
 ,
де
,
де
 -
функція, обернена функції f(z).
-
функція, обернена функції f(z).
Наведемо
без доведення теорему
про диференційовність основних
елементарних функцій комплекснї змінної:
функції
 ,
,
 z,
z,
 z,
z,
 z,
z,
 z,
z,

 диференційовні в будь-якій точці
комплексної площини; функції w=tg z і w=th
z також диференційовні в будь-якій точці
площини, крім точок
диференційовні в будь-якій точці
комплексної площини; функції w=tg z і w=th
z також диференційовні в будь-якій точці
площини, крім точок
 і
і


 відповідно; для функцій w=Ln z, w=
відповідно; для функцій w=Ln z, w= в околі кожної точки
в околі кожної точки
 можна виділити однозначну вітку, яка є
диференційовною в точці z функцією.
можна виділити однозначну вітку, яка є
диференційовною в точці z функцією.
