3. Ряд Тейлора

Теорема 3.3. Всяка аналітична в крузі функція може бути єдиним чином розкладена в цьому крузі в степеневий ряд

(3.7)

коефіцієнти якого визначаються формулами

(3.8)

де - довільне коло з центром у точці , що лежить усередині круга.

Степеневий ряд (3.7) називається рядом Тейлора для функції в розглянутому крузі.

Візьмемо довільну точку усередині даного круга і проведемо коло з центром у точці і радіусом так, щоб точка знаходилася усередині круга (див. рис. 14).

Оскільки функція аналітична в крузі і на його межі , то її значення в точці можна знайти за формулою Коші (2.9): , де - точка на колі . Маємо:

Рис. 14

.Так як , то , отже, вираз можна розглядати як суму членів нескінченно спадної геометричної прогресії з першим членом і знаменником . Таким чином,

Помножимо обидві частини цієї рівності на величину і проінтегруєм її почленно по контуру . Отримаємо:

,

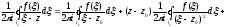
тобто , або , де .

Таким чином, ми одержали розклад функції в степеневий ряд (3.7), коефіцієнти якого визначаються за формулами (3.8).

Доведемо єдиність цього розкладу.

Припустимо, що функція 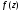в крузі подана іншим степеневим рядом

Послідовно диференціюючи почленно цей ряд нескінченне число раз, будемо мати:

,

,

,

,

,

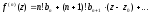Поклавши в цих рівностях, а також у початковому ряді , отримаємо: , , , …, , … Порівнюючи знайдені коефіцієнти ряду з коефіцієнтами ряду (3.7), встановлюємо, що , а це означає, що зазначені ряди збігаються.

Функція 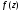розкладається в степеневий ряд єдиним чином.

Наведемо розклад деяких елементарних функцій в ряд Тейлора (Маклорена):

,

,

,

,

Перші три розклади справедливі у всіх точках комплексної площини, останні два – у крузі .

Замінивши на в розкладі функції , отримаємо:

,

тобто формулу Ейлера: .

3. Нулі аналітичної функції

Як показано вище, усяка функція 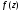, аналітична в околі точки 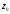, розкладається в цьому околі в степеневий ряд (3.7); коефіцієнти якого визначаються за формулами (3.8).

Точка називається нулем функції , якщо . У цьому випадку розклад функції в околі точки 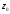в степеневий ряд не містить нульового члена, тому що . Якби не тільки , але і , а , то розклад функції в околі точки має вигляд

, (3.9)

а точка називається нулем кратності (або нулем -го порядку). Якщо , то називається простим нулем.

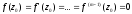З формул (3.8) для коефіцієнтів ряду Тейлора випливає, що якщо є нулем кратності функції , то , але . У цьому випадку функцію можна подати у вигляді , де

(3.10)

Для функції точка вже не є нулем, тому що .

Справедливо і обернене твердження: якщо функція має вигляд (3.10), де – натуральне число, а аналітична в точці , причому , то точка є нуль кратності функції .