
- •§ 16. Елементи теорії функцій комплексної змінної
- •16.1 Функції комплексної змінної.
- •16.1.1. Основні поняття
- •16.1.2 Границя і неперервність функції комплексної змінної
- •16.1.3. Основні елементарні функції комплексної змінної
- •16.1.3.1. Показникова функція
- •16.1.3.2. Логарифмічна функція
- •16.1.3.5. Тригонометричні функції
- •16.1.3.6. Гіперболічні функції
- •16.1.3.7. Обернені тригонометричні і гіперболічні функції
- •16.1.4. Диференціювання функції комплекснї змінної. Умови Ейлера-Даламбера.
- •16.1.5. Аналітична функція. Диференціал
- •16.1.6. Геометричний зміст модуля і аргумента похідної. Поняття про конформне відображення
- •Приклади конформних відображень, що здійснюються деякими елементарними функціями див. Додаток 1.
- •16.2. Інтегрування функції комплексної змінної
- •16.2.1 Означення, властивості і правила обчислення інтеграла
- •16.2.2. Теорема Коші. Первісна , невизначений інтеграл. Формула Ньютона-Лейбніца.
- •16.2.3. Інтеграл Коші. Інтегральна формула Коші
- •16.3. Ряди в комплексній площині
- •16.3.1. Числові ряди
- •16.3.2. Степеневі ряди
- •Ряд Тейлора
- •Нулі аналітичної функції
- •Ряд Лорана
- •Ряд Лорана для функції
- •○ Скористаємося відомим розкладом
- •16.3.6. Класифікація особливих точок. Зв'язок між нулем і полюсом функції
- •Усувні особливі точки
- •Істотно особлива точка
- •16.4. Лишок функції
- •16.4.1. Поняття лишка і основна теорема про лишки
- •16.4.2. Обчислення лишків. Застосування лишків в обчисленні інтегралів
16.1.5. Аналітична функція. Диференціал
Фундаментальним поняттям у теорії функцій комплексної змінної є поняття аналітичної функції.
Однозначна
функція f(z)
називається
аналітичною
(голоморфною)
у
точці z,
якщо вона диференційовна (виконані
умови Ейлера-Даламбера) у деякому околі
цієї точки. Функція f(z)
називається
аналітичною
в області D,
якщо вона диференційовна в кожній точці
 .
.
Як видно з цього означення, умова аналитичності в точці не збігається з умовою диференційовності функції в цій же точці (перша умова більш сильніша).
Точки площини z, у яких однозначна функція f(z) аналітична, називаються правильними точками f(z). Точки, у яких функція f(z) не є аналітичною, називаються особливими точками цієї функції.
Нехай
функція w=f(z)
аналітична в точці
z.
Тоді
 .
Звідси випливає, що
.
Звідси випливає, що
 ,
де
,
де
 при
при
 ,
а приріст функції можна записати так:
,
а приріст функції можна записати так:
 .
Якщо
.
Якщо
 ,
то перший доданок
,
то перший доданок
 являється при
являється при
 нескінченно малою того ж порядку, що і
нескінченно малою того ж порядку, що і
 ;
другий доданок
;
другий доданок
 є нескінченно мала вищого порядку, ніж
є нескінченно мала вищого порядку, ніж
 .
Отже, перший доданок складає головну
частину приросту функції w=f(z).
.
Отже, перший доданок складає головну
частину приросту функції w=f(z).
Диференціалом
dw
аналітичної
функції w=f(z)
у точці
z називається
головна частина її приросту, тобто
 ,
або
,
або
 ,
тобто похідна функції дорівнює відношенню
диференціала функції до диференціала
незалежної змінної.
,
тобто похідна функції дорівнює відношенню
диференціала функції до диференціала
незалежної змінної.
Зауваження.
Якщо
функція
 аналітична в деякій області D, то функції
u(x;y)
і
v(x;y)
задовольняють диференціальному рівнянню
Лапласа (
аналітична в деякій області D, то функції
u(x;y)
і
v(x;y)
задовольняють диференціальному рівнянню
Лапласа ( ).
).
Дійсно, диференціюючи першу з рівностей Ейлера-Даламбера по y, а другупо x, отримаємо:
 ,
,
 ,
,
звідси
 .
.
Функції u(x;y) і v(x;y) називаються гармонічними функціями.
Приклад
3.
Перевірити,
чи є функція
 аналітичною. Знайти її похідну.
аналітичною. Знайти її похідну.
○ Знаходимо
дійсну
 і уявну
і уявну
 частини функції:
частини функції:
 .
.
Таким
чином,
 ,
,
 .
Перевіряємо
умови Ейлера-Даламбера (1.5):
.
Перевіряємо
умови Ейлера-Даламбера (1.5):
 ,
,
 ;
;

 ,
,
 .
.
Умови
(1.5)
виконуються у всіх точках комплексної
площини z.
Функція
 диференційовна, отже, аналітична у всіх
точках цієї площини. Її похідну знайдемо
за однією з формул (1.6), наприклад за
першію:
диференційовна, отже, аналітична у всіх
точках цієї площини. Її похідну знайдемо
за однією з формул (1.6), наприклад за
першію:
 ,
,
тобто
 .
.
Замітимо,
що похідну функції
 можна знайти, скориставшись означенням
похідної (1.4):
можна знайти, скориставшись означенням
похідної (1.4):
 . ●
. ●
Приклад
4.
Знайти аналітичну функцію w=u+iv
за
її заданою дійсною частиною
 .
.
○ Відзначимо,
що функція u
є гармонічною функцією ( ,
,
 ,
отже,
,
отже,
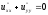 ).
).
Для
визначення уявної частини v
скористаємося
умовами Ейлера-Даламбера (1.5).
Оскільки
 ,
то, згідно першій умові,
,
то, згідно першій умові,
 . Звідси, інтегруючи по y,
знаходимо:
. Звідси, інтегруючи по y,
знаходимо:
 .
.
Для
визначення функції
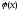 скористаємося другою умовою
Ейлера-Даламбера. Оскільки
скористаємося другою умовою
Ейлера-Даламбера. Оскільки
 ,
,
 ,
,
то
 .
Звідси
.
Звідси
 і
і
 ,
де C
= const.
Тому
,
де C
= const.
Тому
 .
Знаходимо функцію w=u+iv:
.
Знаходимо функцію w=u+iv:
 ●
●
16.1.6. Геометричний зміст модуля і аргумента похідної. Поняття про конформне відображення
Нехай
функція w=f(z)
аналітична в точці
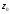 і
і
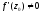 .
З'ясуємо геометричний зміст аргумента
і модуля похідної.
.
З'ясуємо геометричний зміст аргумента
і модуля похідної.
Функція
w=f(z)
відображає
точку
 площини z
у
точку
площини z
у
точку
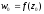 площини
w.
площини
w.
Нехай
довільна точка
 з околу точки
з околу точки
 переміщується до точки
переміщується до точки
 по деякії неперервній кривій l.
Тоді в площині w
відповідна точка
по деякії неперервній кривій l.
Тоді в площині w
відповідна точка
 буде переміщуватися до точки
буде переміщуватися до точки
 по деякій кривій L,
що є образом кривої l
у
площині
w (рис.
4).
по деякій кривій L,
що є образом кривої l
у
площині
w (рис.
4).


Рис. 4
За
означенням
похідної
 .
Звідси випливає, що
.
Звідси випливає, що
 .
Величина
.
Величина
 являє собою відстань між точками
являє собою відстань між точками
 і
і
 ,
а
,
а
 - відстань між точками
- відстань між точками
 і
і
 .
Отже,
.
Отже,
 є границя відношения нескінченно малої
відстані між точками
є границя відношения нескінченно малої
відстані між точками
 і
і
 до нескінченно малої відстані між
точками
до нескінченно малої відстані між
точками
 і
і
 .
Ця границя не залежить (f(z)
аналітична в точці
.
Ця границя не залежить (f(z)
аналітична в точці
 )
від вибору кривої l,
що проходить через точку
)
від вибору кривої l,
що проходить через точку
 .
Отже, границя
.
Отже, границя
 в точці
в точці
 постійна, тобто однакова у всіх напрямках.
постійна, тобто однакова у всіх напрямках.
Звідси
випливає геометричний
зміст
модуля похідної: величина
 визначає коефіцієнт розтягання
(подібності) у точці
визначає коефіцієнт розтягання
(подібності) у точці
 при відображенні w=f(z).
Величину
при відображенні w=f(z).
Величину
 називають коефіцієнтом
розтягу,
якщо
називають коефіцієнтом
розтягу,
якщо
 ,
чи
коефіцієнтом стиску,
якщо
,
чи
коефіцієнтом стиску,
якщо
 .
.
Приклад
5.
Знайти
коефіцієнт розтягу
(стиску)
для функції
 в точці
в точці
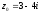 .
.
○ Функція
 аналітична в точці
аналітична в точці
 ,
при цьому
,
при цьому
 .
Отже,
.
Отже,
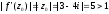 .
Коефіцієнт розтягу для функції
.
Коефіцієнт розтягу для функції
 в точці
в точці
 дорівнює 5 (площина розтягується).
дорівнює 5 (площина розтягується).
Для
аргументу похідної в точці
 маємо:
маємо:
 ,
,
де й а1 і а2 – кути, що утворюють дотичні до кривих l і L відповідно в точках z0 і w0 з додатніми напрямками дійсних осей на площинах z і w (див. рис. 4).
Звідси
 .
Це означає, що
.
Це означає, що
 -
це кут, на який потрібно повернути
дотичну до кривой l
у точці z0
для того, щоб одержати напрямок дотичної
до кривой L
у
точці
w0.
Іншими словами,
-
це кут, на який потрібно повернути
дотичну до кривой l
у точці z0
для того, щоб одержати напрямок дотичної
до кривой L
у
точці
w0.
Іншими словами,
 -
це кут між відображеним і початковим
напрямками дотичних до кривих l
і L
у
точках z0
і
w0
відповідно. У цьому полягає геометричний
зміст
аргументу похідної
-
це кут між відображеним і початковим
напрямками дотичних до кривих l
і L
у
точках z0
і
w0
відповідно. У цьому полягає геометричний
зміст
аргументу похідної
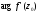 .
●
.
●
В наслідок
аналітичності функції f(z)
у точці
z0
(ми припустили, що )
кут
)
кут
 той
самий для всіх кривих, що проходять
через точку z0.
Для іншої пари кривих l1
і
L1
у тих же точках z0
і
w0
будемо мати
той
самий для всіх кривих, що проходять
через точку z0.
Для іншої пари кривих l1
і
L1
у тих же точках z0
і
w0
будемо мати
 .
Таким чином,
.
Таким чином,
 ,
тобто якщо криві l
і
l1
утворюють у точці z0
на
площині
z
кут
,
тобто якщо криві l
і
l1
утворюють у точці z0
на
площині
z
кут
 ,
то такий же кут
,
то такий же кут
 будуть утворювати в точці w0
криві L
і
L1,
що є образами кривих l
і
l1
на площині w
(див. рис. 5).
будуть утворювати в точці w0
криві L
і
L1,
що є образами кривих l
і
l1
на площині w
(див. рис. 5).
Ця властивість відображення w=f(z) називається властивістю збереження (консерватизму) кутів в точці z0.
Відображення w=f(z), що зберігає кути та коефіцієнт деформації у точці z0, називається конформним (тобто відображенням, що зберігає форму).

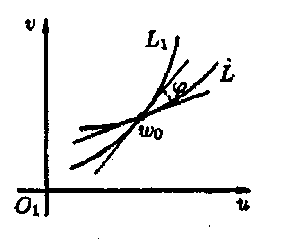
Рис. 5
Якщо при цьому зберігається і напрямок відліку кутів, то таке відображення називається конформним відображенням 1-го роду; якщо напрямок відліку кутів змінюється на протилежний – конформним відображенням 2-го роду.
Таким чином, якщо функція f(z) є аналітичною в деякій точці z0 комплексної площини z і в цій точці її похідна відмінна від нуля, то відображення w=f(z) конформне в цій точці.
Відображення w=f(z) називається конформним в області D, якщо воно конформне в кожній точці цієї області.
Справедливе
наступне твердження: якщо функція
w=f(z)
аналітична
в області
D,
причому у всіх точках області
 ,
то відображення конформне в D;
якщо відображення
w=f(z)
конформне в області
D,
то функція
w=f(z)
аналітична в
D і
в усіх точках цієї області
,
то відображення конформне в D;
якщо відображення
w=f(z)
конформне в області
D,
то функція
w=f(z)
аналітична в
D і
в усіх точках цієї області
 .
.
Приклад 6. З'ясувати геометричну картину відображення, здійснюваного функцією w=2z.
○ Відображення
w=2z
конформне
в усіх точках площини z,
тому що
 .
.
Коефіцієнт
розтягування в будь-якій точці площини
z
дорівнює 2. Оскільки
 ,
то напрямок при відображенні не міняється.
Таким чином, відображення
,
то напрямок при відображенні не міняється.
Таким чином, відображення
 є
перетворення гомотетії з центром у
нульовій точці (w=0
при
z=0)
і коефіцієнтом гомотетії, що дорівнює
2. ●
є
перетворення гомотетії з центром у
нульовій точці (w=0
при
z=0)
і коефіцієнтом гомотетії, що дорівнює
2. ●
