- •Поняття математичної статистики
- •Основні задачі мат. Статистики
- •Статистичний розподіл вибірки
- •23. Як визначаються мода та медіана у випадку, коли дані вибірки згруповані по інтервалах?
- •25. Точкова оцінка.
- •26. Основні властивості оцінок.
- •28. Конзистентність (слушність) оцінки.
- •29. Ефективність оцінки.
- •31.Чи є оцінка для дисперсії незміщеною, консистентною та ефективною?
- •32.Теорема про незміщеність емпіричних початкових моментів.(Доведення)
- •41. Метод максимальної правдоподібності побудови точкових оцінок.
- •75. Етапи перевірки статистичних гіпотез:
- •76. Визначення області прийняття гіпотези та критичну область для гіпотези при альтернативі
- •77. Визначення області прийняття гіпотези та критичну область для гіпотези при альтернативі .
- •78. Визначення області прийняття гіпотези та критичну область для гіпотези (при альтернативі
- •103. Побудова довірчого інтервалу для
- •104. Вибіркова коваріація
- •105. Вибірковий коефіцієнт кореляції, властивості
32.Теорема про незміщеність емпіричних початкових моментів.(Доведення)
Емпіричні початкові моменти є незміщеною оцінкою відповідних елементів генеральної сукупності, при умові якщо вони існують.
![]()
Для емпіричного початкового моменту n-ого порядку ми маємо:

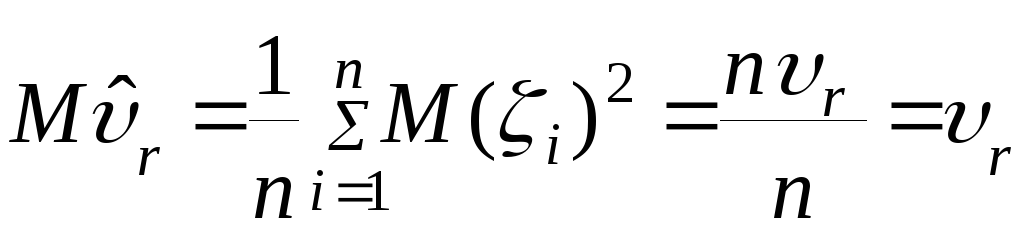
Нехай
в нас є
![]() -
незміщена оцінка параметра
-
незміщена оцінка параметра
![]() ,
тоді необхідно і достатньо, що умовою
збіжності оцінки
,
тоді необхідно і достатньо, що умовою
збіжності оцінки
![]() є
збіжність дисперсії оцінки до 0.
є
збіжність дисперсії оцінки до 0.
![]()
Доведення аналогічне доведенню нерівності Чебишева.
-
немає
34.Означення кількості інформації за Фішером.
Функцію
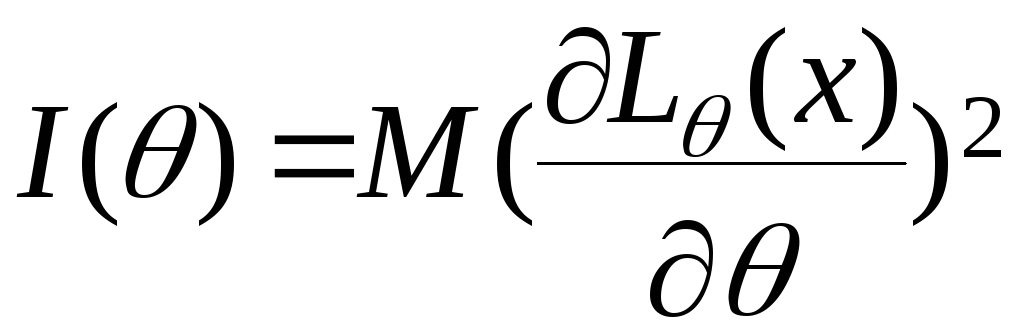 називають кількістю інформації за
Фішером.
називають кількістю інформації за
Фішером.
![]()
 -
щільність
-
щільність
35.Лема
про рівність
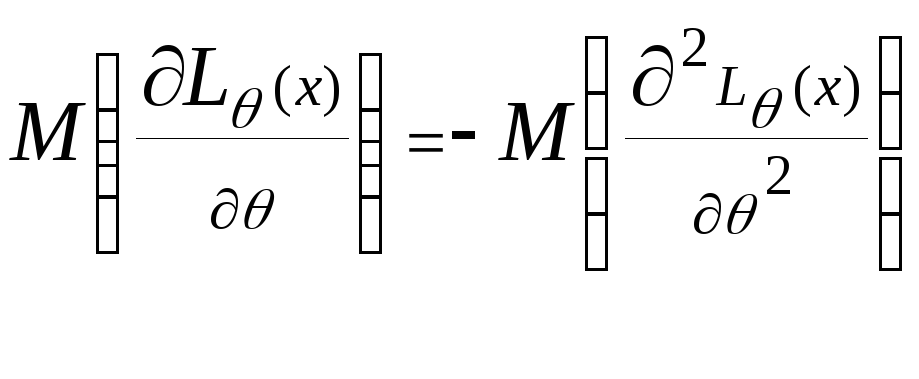 .
(Доведення загальний випадок)
.
(Доведення загальний випадок)
Якщо
майже для всіх
![]() існують похідні
існують похідні
 ,
які є мажорвні інтегрованим функціям
,
які є мажорвні інтегрованим функціям
![]() і виконується умова
і виконується умова
 ,
то для всіх
,
то для всіх
![]()
 ,
а
,
а
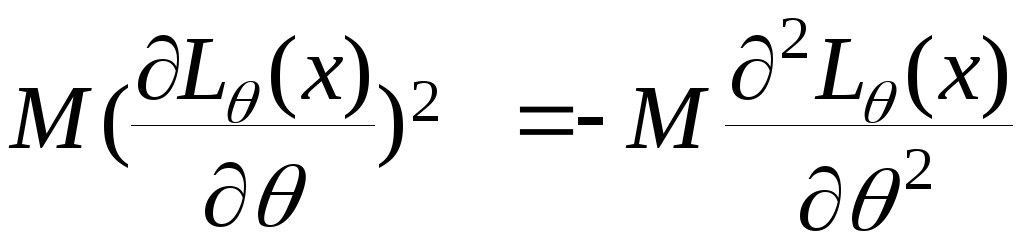
Доведення
Використовуючи властивості функції щільності зазначимо:
![]()
Візьмемо похідну і маємо:
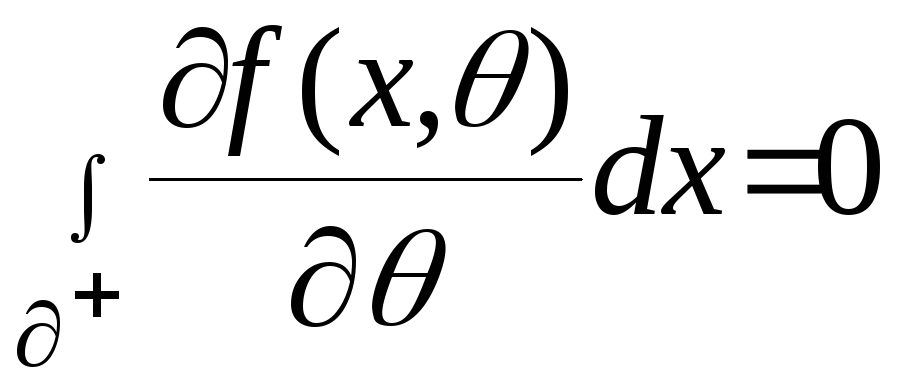
Введемо наступні позначення:
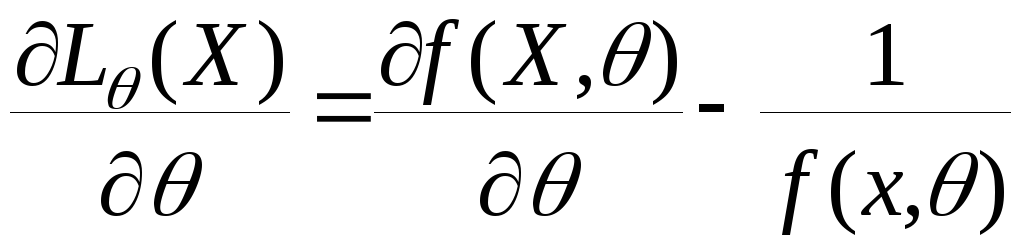
Маємо:
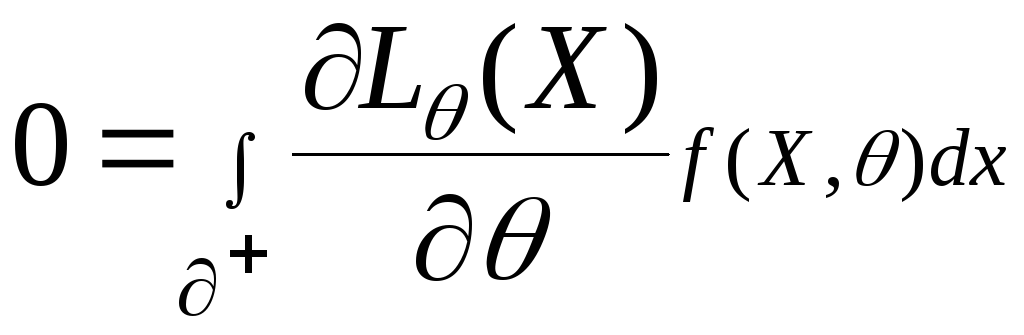
Візьмемо
другу похідну по
![]() :
:
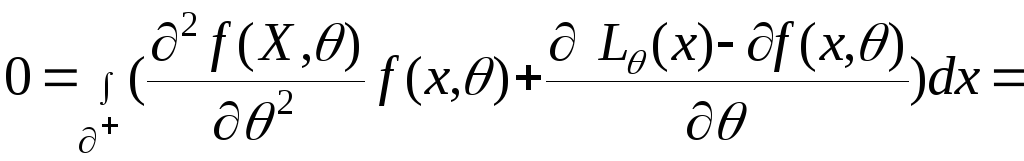
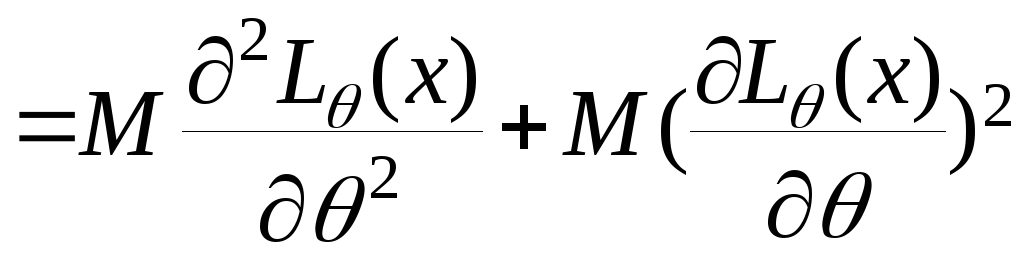
Звідси ми отримуємо
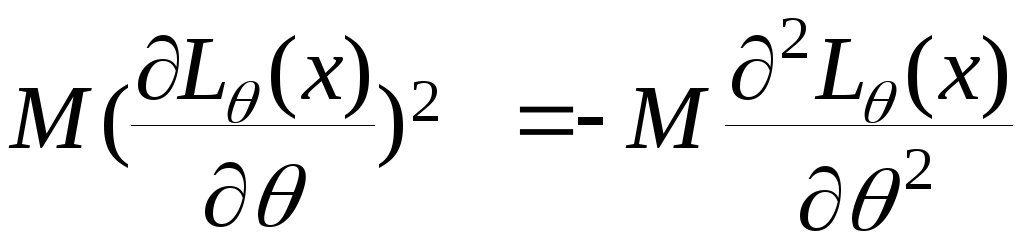
Теорему доведено.
36.Теорема про нерівність Крамера-Рао (загальний випадок). Доведення.
Нехай
задовольняються умови леми про рівність
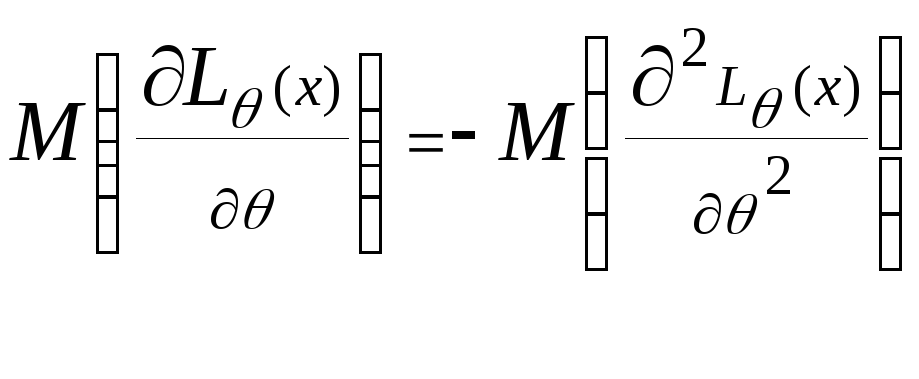 і
і
![]() -
незміщена оцінка параметра
-
незміщена оцінка параметра
![]() ,
така що функція
,
така що функція
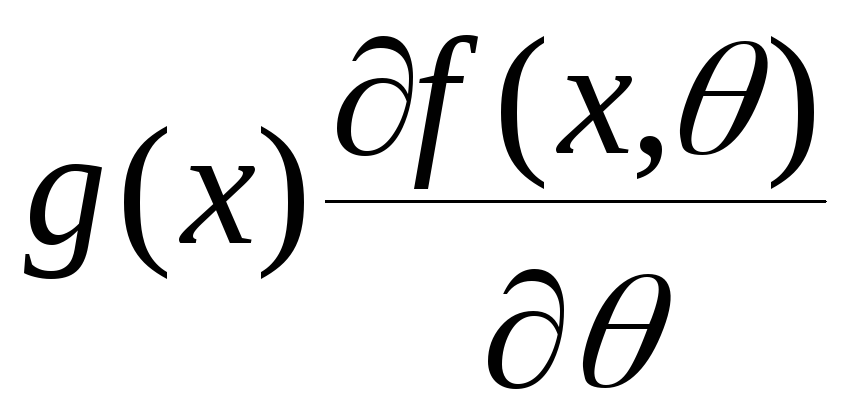 ,
,![]() мажоровна інтегрованою функцією
мажоровна інтегрованою функцією
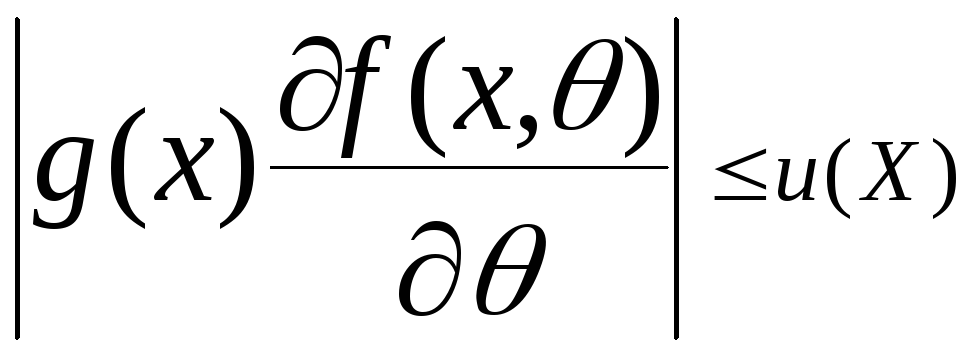 ,
,
![]() ,
тоді виконується нерівність:
,
тоді виконується нерівність:
 ,
де величина
,
де величина
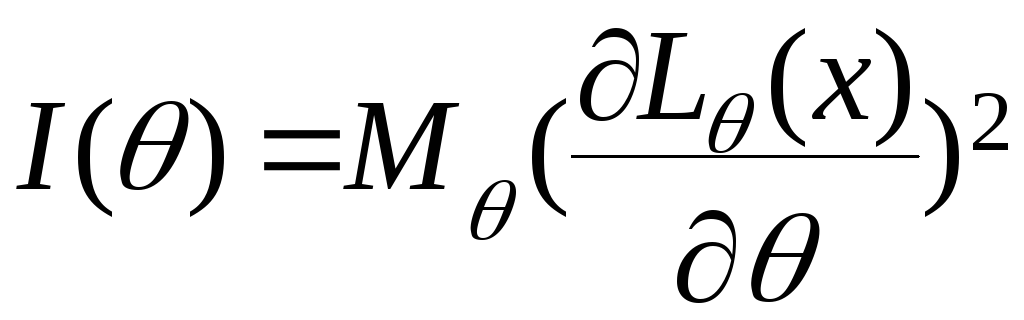 -
кількість інформації за Фішером.
-
кількість інформації за Фішером.
Причому
рівність досягається тоді і тільки
тоді,коли
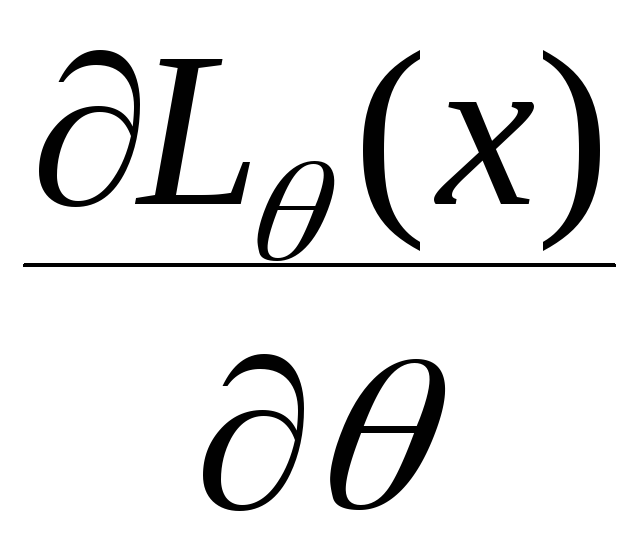 можна подати у вигляді
можна подати у вигляді
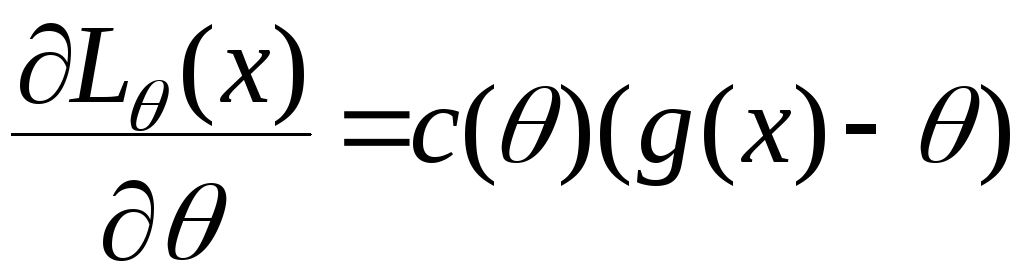 .
.
37.Наслідок теореми (про нерівність Крамера-Рао) про ефективність оцінки.
Якщо
для оцінки
![]() виконується нерівність Крамера-Рао,
зокрема перетворення на рівність, то
оцінка
виконується нерівність Крамера-Рао,
зокрема перетворення на рівність, то
оцінка
![]() є ефективною.
є ефективною.
38.Лема
про рівність
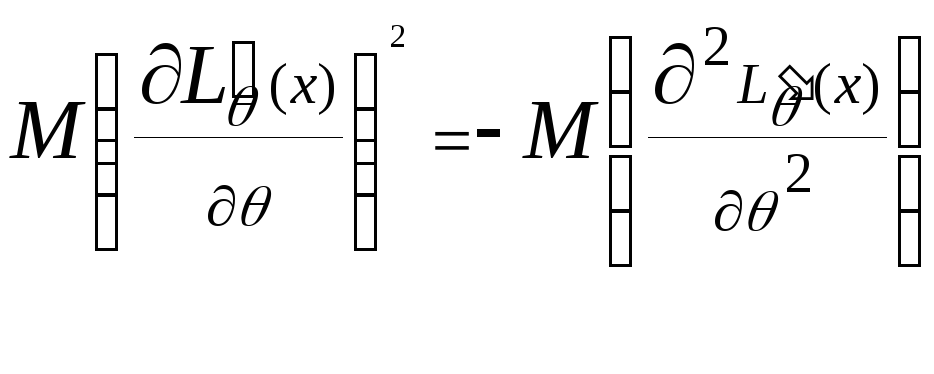 (для дискретного розподілу). Доведення.
(для дискретного розподілу). Доведення.
Якщо
майже для всіх можливих значень
![]() вибірки
вибірки
![]() існують похідні
існують похідні
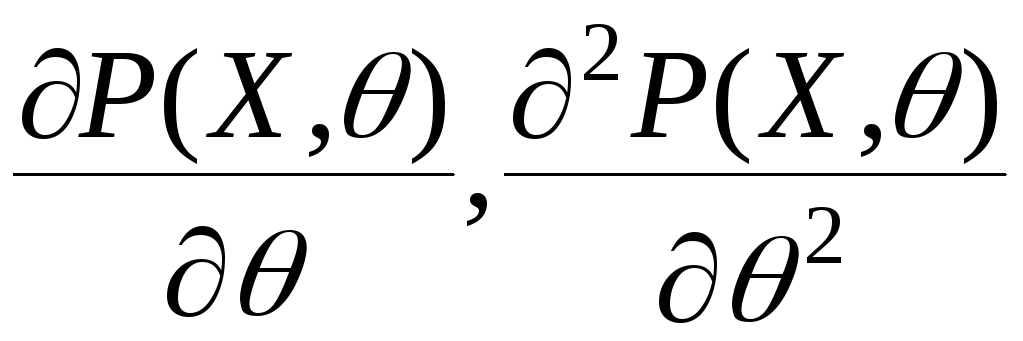 ,
,![]() .
.
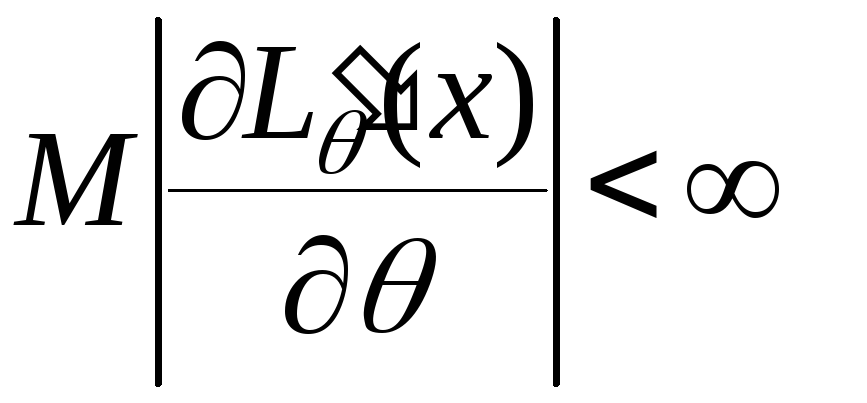 ,
,
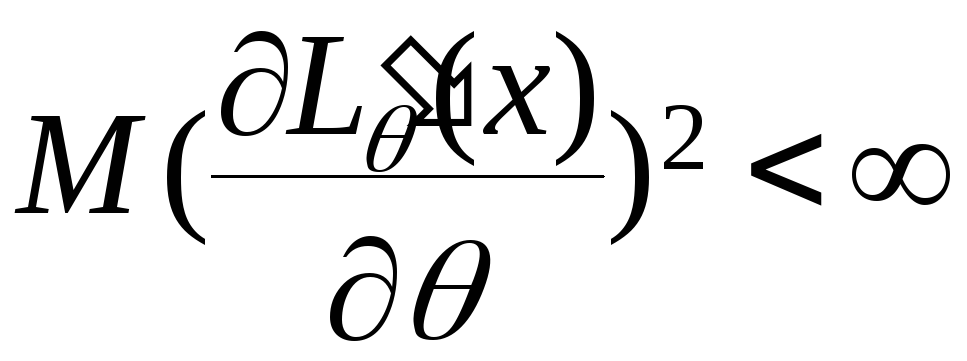 ,
,
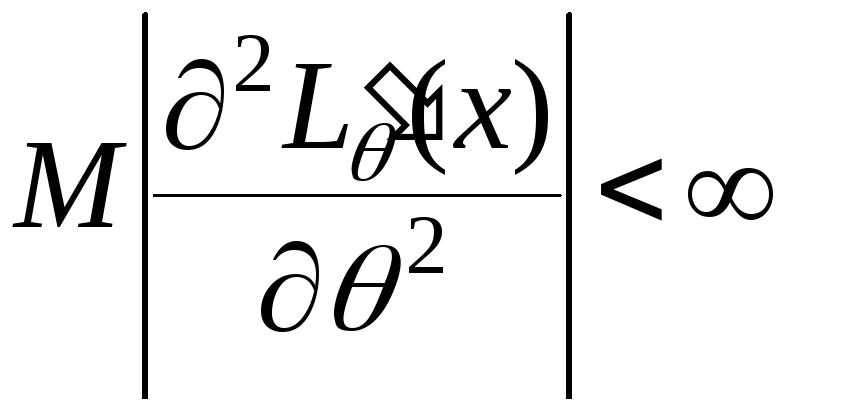 ,
,![]() ,
то для всіх
,
то для всіх
![]() :
:
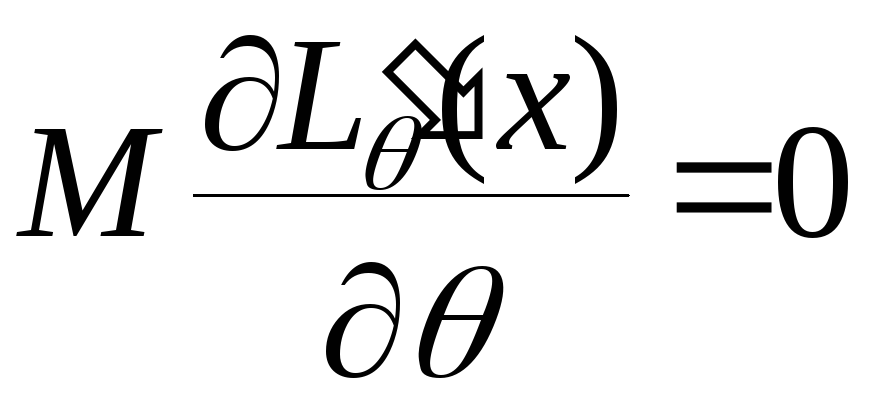 ,і
,і
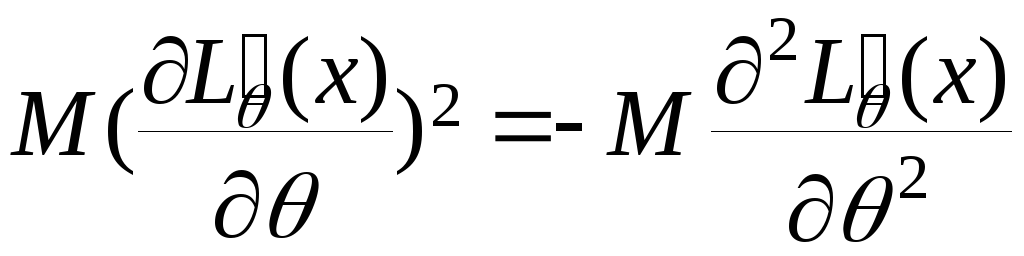 ,
де
,
де
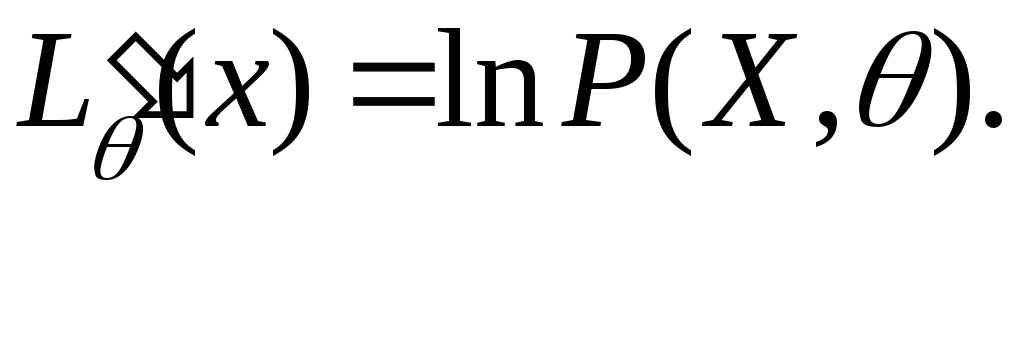
Доведення аналогічне до леми в питанні 35.
39.Теорема про нерівність Крамера-Рао (дискретний розподіл). Доведення.
Нехай
задовольняються умови леми про рівність
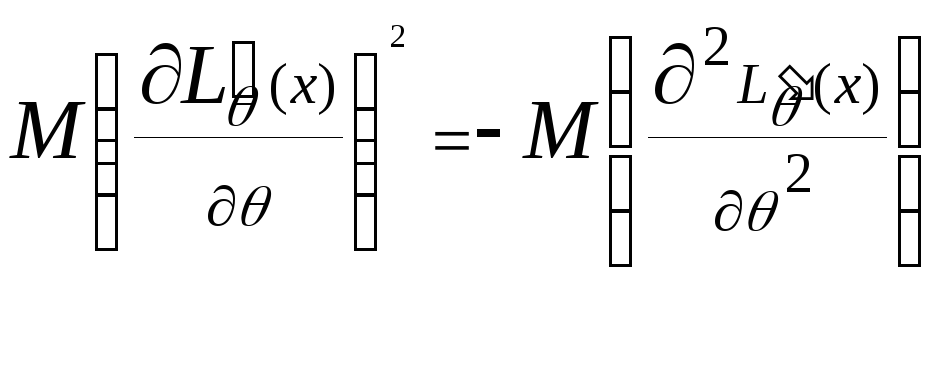 (для дискретного розподілу) і
(для дискретного розподілу) і
![]() -
незміщена оцінка параметра
-
незміщена оцінка параметра
![]() така що функція для всіх можливих значень
така що функція для всіх можливих значень
![]() вибірки
вибірки
![]() і ряд
і ряд
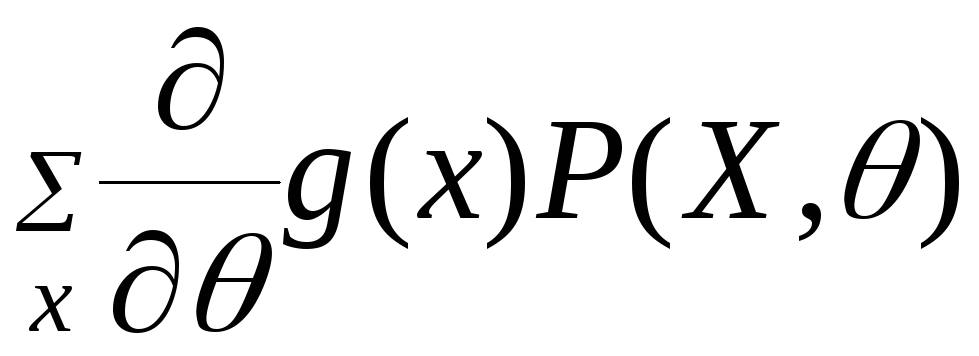 збігається абсолютно і рівномірно
збігається абсолютно і рівномірно
![]() .
.
Тоді
виконується нерівність
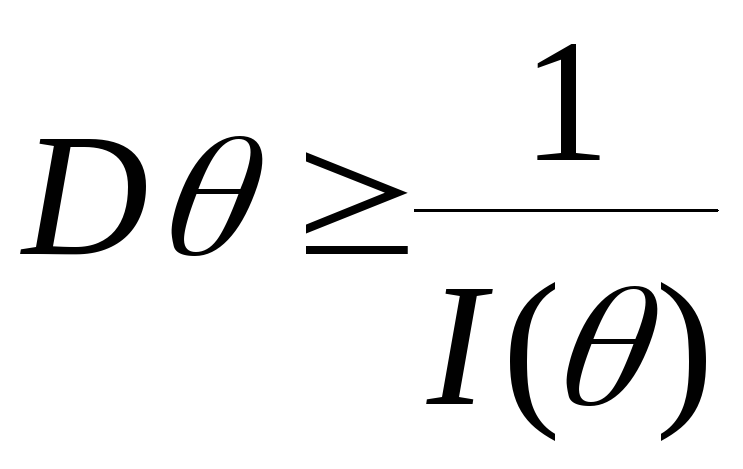 ,
причому рівність справджується тоді і
тільки тоді, коли
,
причому рівність справджується тоді і
тільки тоді, коли
 можна подати у вигляді
можна подати у вигляді
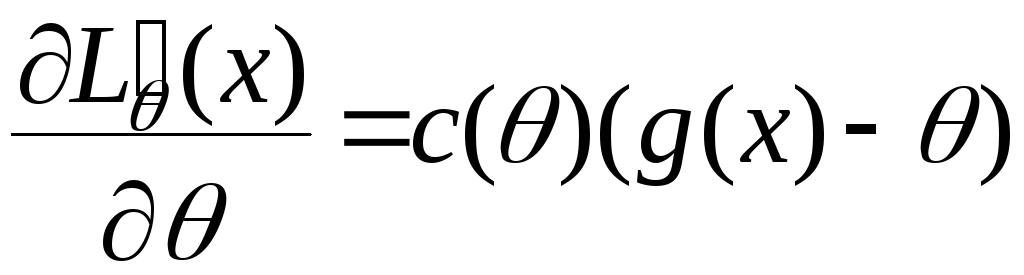
Доведення аналогічне як у питанні 36.
40.Метод моментів побудови точкових оцінок.
Нехай
в нас є вибірка
![]() ,
,
![]() ,
де розподіл залежить від параметру
,
де розподіл залежить від параметру
![]() який в свою
чергу
є вектором S
який в свою
чергу
є вектором S
![]() .
Нам потрібно оцінити невідомі параметри
.
Нам потрібно оцінити невідомі параметри
![]() .
.
Першим загальним методом побудови оцінок невідомих параметрів за вибіркою є метод моментів, що запропонований Пірсоном.
Взагалі
можна показати, що початковий та
центральний емпіричні моменти є
конценстендними оцінками відповідно
початкового і центрального моментів
першого порядку. Згідно з методом
моментів певну кількість вибіркових
моментів
![]() прирівнюють до відповідних моментів
прирівнюють до відповідних моментів
![]() ,розподілу
,розподілу
![]() .
.
Ці
вибіркові моменти обчислюються при
значеннях параметрів
![]() ,
що дорівнюють відповідно
,
що дорівнюють відповідно
![]() .
.
Перший вибірковий момент:
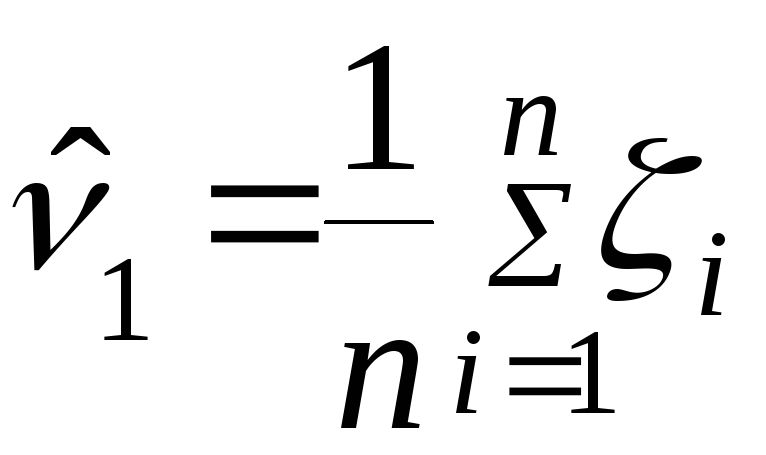

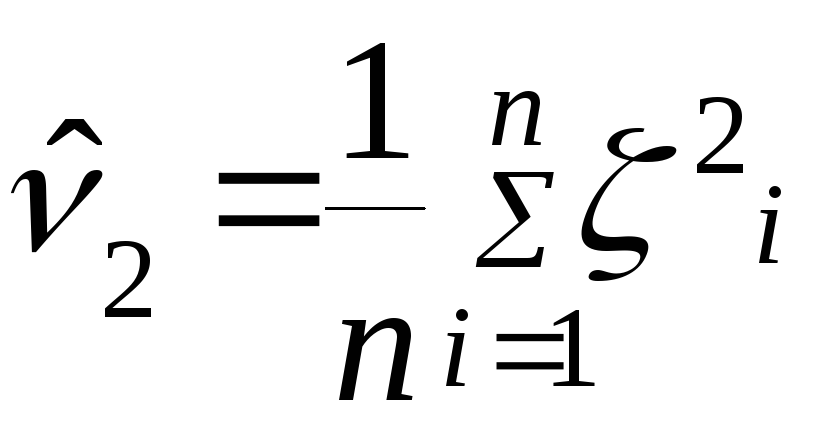
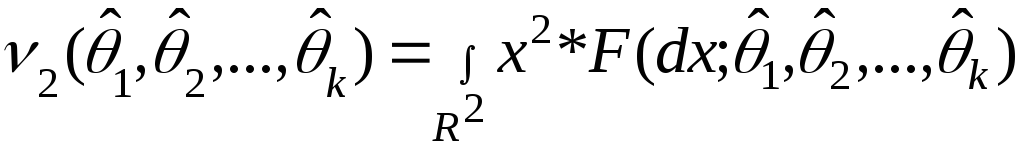
Розглянемо кількість початкових моментів, що дорівнює кількості невідомих параметрів, які потрібно оцінити, обертають таку саму кількість рівнянь для визначення невідомих параметрів.