Численные методы

2.2. Отделение корней уравнения

Графический метод

Отделить корень х* уравнения f(x) = 0 – значит указать окрестность точки x* (отрезок [a, b]), не содержащую других корней этого уравнения.

Очевидно, что найти корень уравнения (1) означает найти абсциссу точки пересечения графика y = f(x) с прямой у = 0, т. е. осью абсцисс. При этом если построение y = f(x) затруднительно, то ее представляют в эквивалентном виде:

f1(x) = f2(x)

с таким расчетом, чтобы графики y1 = f1(x) и y2 = f2(x) строились проще.

Абсциссы их точек пересечения и будут корнями уравнения (1).
Пример 1. Рассмотрим в качестве примера уравнение (2 x)2 ex					0,5.
Приведем	его	к стандартному виду	(1):	(2 x)2 ex 0,5 0,	где
f (x) (2 x)2	ex 0,5. Так как при построении графика функции f(x) вруч-
ную могут	возникнуть трудности, то, согласно			(3), запишем его	как
(2 x)2 0,5 ex .		Построим графики функций	f1(x) (2 x)2 и f2(x) e x 0,5
(рис 1).

Рис 1. Пример графического отделения корней

10

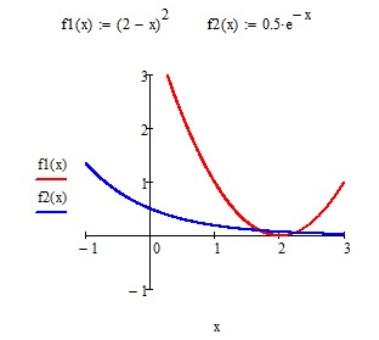
На рис. 1 видно, что данное уравнение имеет 3 корня. Первый из них, очевидно, принадлежит промежутку х1 [-5, -3]. Для нахождения промежутков, на которых расположены два оставшихся корня, увеличим масштаб построения графиков (рис 2.).

Рис 2. Графическое отделение корней

Из рисунка видно, что х2 [1, 2]; х3 [2, 3].

При графическом отделении корней уравнения результат зависит от точности построения графиков.

Аналитический метод

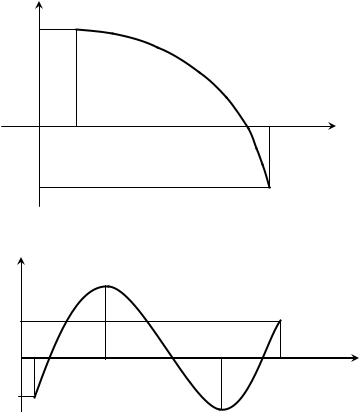
Как известно из анализа, если непрерывная функция f(x) на концах отрезка [a, b] принимает значения разных знаков, т. е. если f(a) f(b) < 0, то внутри этого отрезка существует, по крайней мере, один корень уравнения f(x) = 0 (рис. 3). При этом корень x* будет единственным, если f '(x) сохраняет знак внутри интервала (а, b), т. е. является монотонной (рис. 3.1, а).

11

у

f(a)

	f (x) < 0
		b
a	x*	х

f(b)

а

у

f(b)

0	а		x2	d	b
	x1	c		x3	х

f(a)

б

Рис 3. a – один корень уравнения, b – несколько корней уравнения

Согласно вышеизложенному, получается следующий алгоритм определения корней уравнения f(x) = 0:

1)находим участки возрастания и убывания функции f(x) (с помощью производной f (x), если она существует);

2)составляем таблицу знаков функции f(x) в стационарных точках (или ближайших к ним), а также в граничных точках области определения f(x);

3)определяем границы интервалов, на которых f(x) имеет противоположные знаки. Внутри таких интервалов содержится только по одному корню.

На рис. 3, б интервалы монотонности функции (a, c), (c, d), (d, b), на концах которых функция имеет противоположные знаки. Корнями уравнения f(x) = 0 на отрезке [a, b] в данном случае являются точки x1, x2 и x3.

12

Пример 2. Рассмотрим уравнение из примера 1. С целью экономии времени не будем вручную исследовать функцию f (x) (2 x)2 ex 0,5 на монотонность и определять ее знак на концах промежутков монотонности, а сразу построим ее график в Mathcad (рис. 4).

Рис. 4. График функции f(x)

На рис. 4 интервалы монотонности данной функции: (-∞, 0), (0, ≈2), (≈2, +∞), на концах которых функция имеет противоположные зна-

ки. Корнями уравнения f(x) = 0 в данном случае являются точки x1, x2 и x3 из данных промежутков.

2.3. Уточнение корней уравнения

Метод половинного деления

Алгоритм метода (рис. 5) состоит из следующих операций. Отрезок [a, b] делят пополам точкой c, c = (a+b)/2, и находят значение функции в точке с. Если f(c) = 0, то корень уравнения соответствует точке c. Если f(c) ≠ 0, то можно сузить диапазон поиска корня: перейти от отрезка [a, b] к отрезку [a, c] или [c, b] в зависимости от знака f(c). Если f(a) f(c)<0, то корень находится на отрезке [a, c], и точку с будем считать точкой b; а если f(a) f(c) > 0, то корень находится на отрезке [c, b], и точку с будем считать точкой a.

13

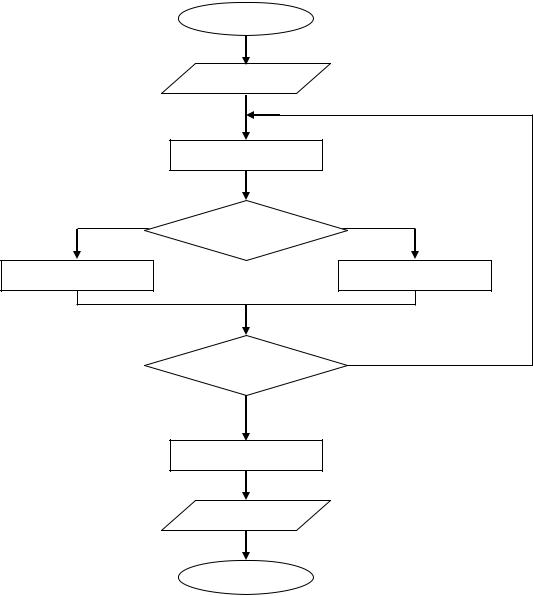
Каждый такой шаг уменьшает в два раза интервал, в котором находится корень уравнения f(x) = 0. После нескольких шагов получится отрезок, длина которого будет меньше или равна числу ε, т. е. |a–b| = <ε. Любая точка такого отрезка, например, один из его концов, подходит в качестве решения поставленной задачи.

	Начало
	Ввод a, b, ε
	c:=(a+b)/2
Нет	f(a)∙f(c)≤0	Да
a:=c		b:=c
	|b-a|≤ ε	нет
	Да
	x:=c
	Вывод x
	Конец

Рис. 5. Блок-схема алгоритма «Метод половинного деления»

Пример 3. Найдем решение уравнения из примера 1 методом половинного деления в Mathcad (рис. 6).

14

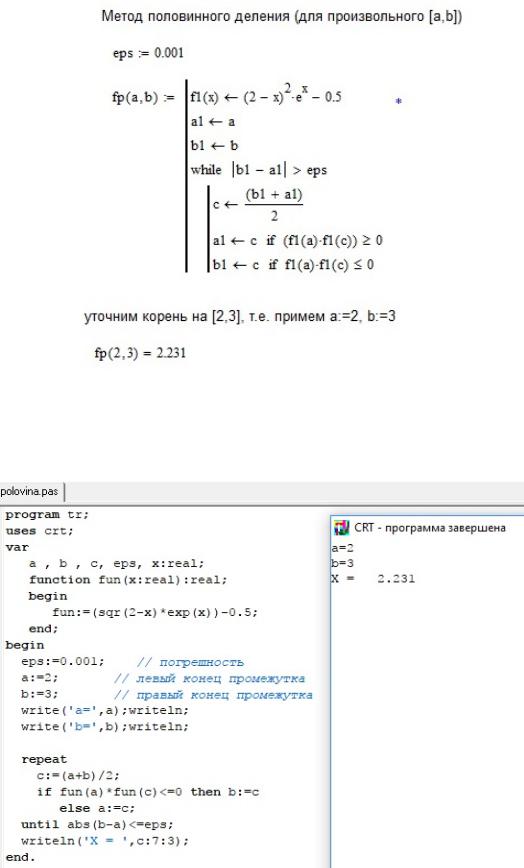
Рис. 6. Пример реализации метода половинного деления в Mathcad

Найдем решение уравнения из примера 1 методом половинного деле-

ния в Pascal ABC (рис. 7).

Рис. 7. Пример реализации метода половинного деления в Pascal ABC

15

Метод Ньютона (метод касательных)

В основе метода лежит разложение функции f(x) в ряд Тейлора: f (xn h) f (xn ) h f (xn ) h22 f (xn ) ...

Члены ряда, содержащие h во второй и более высоких степенях, отбрасываются; используется соотношение xn+h = xn+1. Получаем:

	(3)
f (xn h) f (xn ) (xn 1 xn ) f (xn )

Выражение (3) – уравнение касательной к кривой y = f(x), проведенной через точку с координатами (xn, f(xn)) (рис. 8).

Предполагается, что переход от xn к xn+1 приближает значение функции к нулю так, что f(xn+h) = 0. Значение xn+1 соответствует точке, в которой касательная к кривой в точке xn пересекает ось Ох. Отсюда:

f (x ) xn 1 xn f (xn )

n

Так как кривая f(x) отлична от прямой, то значение функции f(xn+1) не будет в точности равно нулю. Поэтому вся процедура повторяется, причем вместо xn используется xn+1. Счет прекращается, когда разница меж-

ду xn и xn+1 будет меньше или равна числу ε, т. е		xn 1 xn					f (xn )		=<ε.
							f (xn )

Проблематичным является выбор x0 – первого приближения (а точке x0 = a или x0 = b проводить первую касательную к графику функции). Часто при неудачном выборе x0 нет монотонного убывания последовательности |xn+1 – xn|, поэтому рекомендуется за начальное приближение принять такое значение x0 из [a,b], для которого выполняется условие: f (x0) f // (x0) 0, называемое условием Фурье.

Метод Ньютона требует меньшего числа повторений, чем метод половинного деления. Недостатки метода – необходимость дифференцирования функции f(x), и f'(x) должно быть не равно нулю.

16

Рис. 8. Геометрическая интерпретация метода Ньютона (касательных)

Начало

Ввод a, b,

x:=a (или b)

t:=f(x)/f´(x)

x:=x-t

|t|≤	Нет

Да Вывод x

Конец

Рис. 9. Блок-схема алгоритма «Метод Ньютона (метод касательных)»

Пример 4. Найдем решение уравнения из примера 1 методом Ньютона

(касательных) в Mathcad (рис. 10) и в Pascal ABC (рис. 11).

17

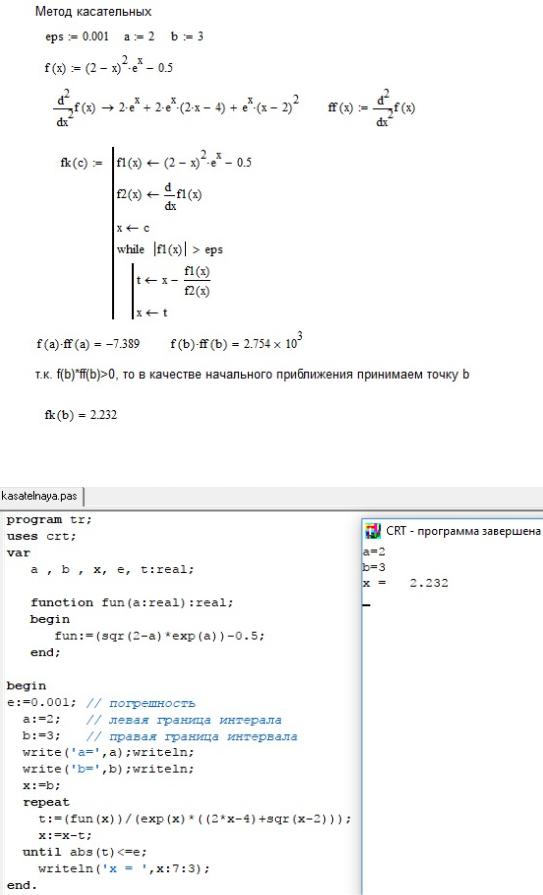
Рис. 10. Пример реализации метода Ньютона (метод касательных) в Mathcad

Рис. 11. Пример реализации метода Ньютона (метод касательных) в Pascal ABC 18

Метод хорд (метод ложного положения)

В основе метода лежит линейная интерполяция по двум значениям функции f(x), имеющим противоположные знаки. Через точки, соединяющие значения функции f(a) и f(b) на концах отрезка [a, b], проводят прямую (хорду). Решение уравнения f(x)=0 приближают абсциссой пересечения хорды с Ох.

y				B
	f(b)
				y = f(x)
	x1 x2 x3
	a		x*	b
			C
f(a)	A	A1		x
			A2
Рис. 12. Геометрическая интерпретация метода хорд

Уравнение прямой АВ можно записать в виде:

	x a				y f (a)
	b a				f (b) f (a)
	x b				y f (b)
						.
	b a			f (b) f (a)

Найдем точку пересечения хорды АВ с Ox (первое приближение)

Находим первое приближение, полагая в (4)				у = 0:
или
x1 a f (a)		b a	,
		f (b) f (a)
или (полагая в (5) y = 0 )
x1 b f (b)		b a		.
		f (b) f (a)

(4)

(5)

(6)

(7)

19