Численные методы

3.3. Индивидуальные задания для лабораторной работы № 2

Самостоятельно задать функцию таблично шестью парами точек (с одинаковым шагом по x). Выполнить лабораторную работу по алгоритму:

1.Записать формулу Лагранжа и Ньютона для таблично заданной функции.

2.Составить программу в Mathcad для расчета по формуле Лагранжа

ивычислить численное значение полинома в заданных точках.

3.Составить программу в Mathcad для расчета по формуле Ньютона

ивычислить численное значение полинома в заданных точках.

4.Сравнить методы Лагранжа и Ньютона, используемых для обработки экспериментальных данных.

5.Обсудить результаты. Сделать выводы по работе.

3.4.Вопросы для самоконтроля

1.Сформулировать задачу интерполирования.

2.Интерполяционная формула, узлы интерполяции.

3.В каких случаях применяется интерполяция?

4.Графическая иллюстрация интерполяции для случая, когда функция задана: a) аналитически; б) таблично.

5.Что такое параболическая интерполяция? Почему она находит широкое применение?

6.В каком случае используют интерполяционный полином Лагранжа? Записать его формулу.

7.Какова степень интерполяционного полинома Лагранжа?

8.Линейная и квадратичная интерполяция, примеры их применения. Их графическая иллюстрация.

30

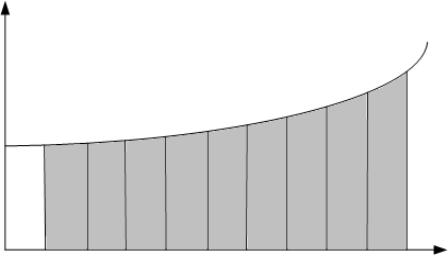
4. ЛАБОРАТОРНАЯ РАБОТА № 3 ВЫЧИСЛЕНИЕ ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ

4.1. Постановка задачи

Необходимость вычисления значений определенных интегралов при моделировании возникает достаточно часто.

Формула Ньютона-Лейбница I *	b	f (x )dx F (b ) F (a ) имеет
	a
ограниченное применение:

–не позволяет вычислить интегралы от таблично заданной подынтегральной функции f(x);

–не всякая интегрируемая функция имеет первообразную F(x), выражаемую в элементарных функциях.

Численные методы интегрирования универсальны: позволяют вычислить значение определенного интеграла непосредственно по значениям подынтегральной функции f(x), независимо от способа ее задания или вида аналитического выражения.

Геометрический смысл: определенный интеграла равен площади криволинейной трапеции, ограниченной осью Oх, кривой f(x) ≥ 0, и прямыми

x= a и x = b.

f

fn

					fn-1
			fi	fi+1	Sn-1
f0	f1
		S2	Si	Si+1
S0	S1
0	1	2	i	i+1	n
a=x0	x1	x2	xi	xi+1	b=xn	x

Рис. 19. Геометрический смысл определенного интеграла

31

Численные методы интегрирования основаны на различных способах оценки этой площади, поэтому полученные формулы численного интегрирования называются квадратурными формулами вычисления площади.

Рассмотрим получение и применение простейших формул.

Отрезок [a, b] делят на n необязательно равных частей – элементарных отрезков. Принято такое деление отрезка называть сеткой, а точки x0, x1,…, xn – узлами сетки.

Если сетка равномерная, то h b n a – шаг сетки, при интегрировании – шаг интегрирования, а координата i-го узла вычисляется по формуле:

xi a i h , где i 0,n.

Полная площадь криволинейной трапеции состоит из n элементарных криволинейных трапеций – элементарных площадей:

n 1

I * S i .

i 0

Квадратурные формулы отличаются друг от друга способом оценки значения Si – площади элементарной криволинейной трапеции.

Рассмотрим получение простейших формул для часто используемой равномерной сетки.

4.2. Формулы прямоугольников

Площадь i-той элементарной трапеции можно оценить (приближенно вычислить) как площадь прямоугольника со сторонами xi 1 xi h и fi. То-

гда Si fi h	и значение интеграла:
	n 1	n 1	n 1	n 1	n 1
I*	Si fi h h fi h f (xi ) h f (a i h).
	i 0	i 0	i 0	i 0	i 0

32

	fi+1
fi	← Погрешность

Si

xi xi+1

Рис. 20. Оценка элементарной площади Si левым прямоугольником.

Полученная формула называется формулой левых прямоугольников, так как для оценки площади использовалось левое основание элементарной криволинейной трапеции. Аналогично можно получить формулу правых прямоугольников:

fi fi+1

Погрешность →

Si

xi xi+1

Рис. 21. Оценка элементарной площади Si правым прямоугольником

Для данного случая Si fi 1 h и тогда значение интеграла:

	n 1	n 1	n	n	n
I *	Si	fi 1	h h fi	h	(xi ) h f (a i h).
	i 0	i 0	i 1	i 1	i 1

Эти формулы не находят широкого применения, так как имеют большую погрешность, пропорциональную величине шага δM O(h)

Как появляется эта погрешность, видно на рисунках.

Для повышения точности площадь Si можно оценить, используя прямоугольник со стороной, равной значению подынтегральной функции в

середине элементарного отрезка	~		h
	fi f xi		2	.
		33

	~	fi+1
	fi	←Погрешностьδ2
	Погрешность δ1 →
	fi
	Si

xi xi+1

Рис. 22. Оценка элементарной площади Si центральным прямоугольником

Для данного случая Si ~fi h и формула центральных прямоугольников имеет вид:

n 1

n 1

~

n-1

~

n-1

h

n-1

h

I* Si fi

h h fi

h f xi

2

h f a i h

2

.

i 0

i 0

i 0

i 0

i 0

Как видно из рис. 22, погрешность в оценке площади Si в данном случае существенно меньше, чем в двух предыдущих (погрешность оценивается разницей площадей δ1 и δ2).

Погрешность метода пропорциональная квадрату величины шага

δM O(h2)

Пример 8. Вычислить значения определённого интеграла по формулам

прямоугольников: I 2,0 x 2 1 dx

0,5

Точное значение легко вычисляется по формуле Ньютона-Лейбница:

		3				2		3					3				8			1			1
		x						2				0,5
I		3	x		0,5			3	2			3		0,5				2		8 3			2		=
																	3
				=		14		13		112 13				99	33		4,125
						3		24		24				24		8		.

Для вычисления интеграла по квадратурной формуле необходимо выбрать число узлов n.

34

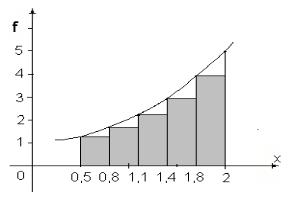
Пусть n = 5, тогда h b a		2 0,5	0,3.
n		5
1. Расчет по формуле левых прямоугольников:
n 1			4
IЛП h f (a i		h) 0,3 f (0,5		i 0,3)
i 0			i 0

0,3 f (0,5) f (0,8) f (1,1) f (1,4) f (1,7)

0,3 (0,52 1) (0,82 1) (1,12 1) (1,42 1) (1,72 1)

0,3 11,95 3,585

Погрешность расчета δ I* IЛП 4,125 3,585 0,540.

Знак и значение погрешности можно легко оценить по геометрической иллюстрации вычисления интеграла по квадратурной формуле.

	Суммарная площадь прямоугольников
f = x² +1	заметно меньше площади криволиней-
	ной трапеции

Рис. 23. Геометрическая иллюстрация вычисления значения определенного интеграла по формуле левых прямоугольников

2. Расчет по формуле правых прямоугольников:

n	5
IПП h f (a i h) 0,3	f (0,5	i 0,3)
i 1	i 1

0,3 f (0,8) f (1,1) f (1,4) f (1,7) f (2,0)

0,3 (0,82 1) (1,12 1) (1,42 1) (1,72 1) (2,02 1)

0,3 1,64 2,21 2,96 3,89 5 4,71

Погрешность расчета δ I* IПП 4,125 4,71 0,585.

Для повышения точности необходимо увеличить n или использовать более точные квадратурные формулы.

35

3. Расчет по формуле центральных прямоугольников:

I ЦП h f		(a i h h ) 0,3 f (i 0,3 0,15)
	n -1		4
	i 0	2	i 0
0,3 (0,65) f (0,95)			f (1,25) f (1,55)	f (1,85)
0	,3 (0,652	1) (0,952	1) (1,252 1) (1,552		1) (1,852	1)
0	,3 1,4225 1,9025 2,5625 3,4025 4			,4225 4,114.

Погрешность расчета δ I* IЦП 4,125 4,114 0,011.

Формула центральных прямоугольников на порядок точнее предыдущих формул.

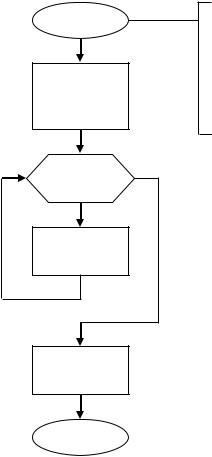
На рис. 24 приведена общая блок-схема для трех вариаций метода прямоугольников.

Начало

h bn-a

S = 0 a = a+k∙h

Входные данные: a – начало отрезка; b – конец отрезка; n – число узлов;

k – вариант метода прямоугольников: k = 0 – левые,

k = ½ –центральные, k = 1 –правые.

i = 0, n-1, 1

S = S+f(a+i∙h)

S = h∙S

Конец

Рис. 24. Блок-схема алгоритма «Метод прямоугольников»

36

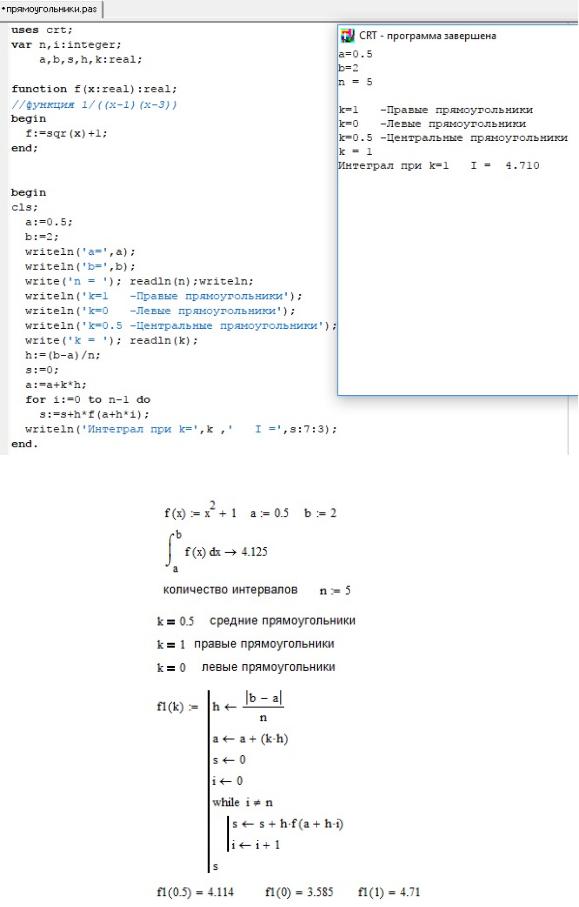
Рис. 25. Пример реализации метода прямоугольников в Pascal ABC

Рис. 26. Пример реализации метода прямоугольников в Mathcad 37

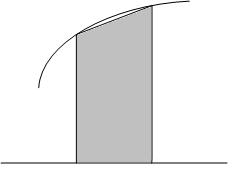
4.3.Формула трапеций

Вданном методе элементарная криволинейная трапеция заменяется трапецией (кривая f(x) заменяется хордой CD).

CDfi+1

fi

Si

xi

xi+1

Рис. 27. Оценка элементарной площади Si трапецией

Из рисунка видно, что Si

fi

fi 1

h.

2

Отсюда

n 1

n 1 f

i

f

i 1

f

0

f

f

f

2

f

2

f

3

I* Si

h h (

1

1

...

2

2

2

2

i 0

i 0

...

fn 2 fn 1

fn 1 fn

)

2

2

f

f

n 1

f (a) f (b)

n 1

h (

0

n

fi ) h

f (a i h)

2

2

i 1

i 1

Погрешность формулы трапеций пропорциональная квадрату шаг h

δM O(h2 ) т. е. формулы центральных прямоугольников и трапеций имеют близкую точность.

Пример 9. Вычислить по формуле трапеций значение ранее рассмот-

ренного определённого интеграла I 2 x2 1 dx при n =5, h = 0,3.

0,5

38

		f (a )				f (b)				n 1						f (0,5)				f (2)					4
I ТР h									f (a i h)							0,3									f (0,5 0,3i)
					2														2
										i 1															i 1
				2			2
(0,5					1)	(2			1)
0,3												f (0,8)		f (1,1) f (1,4)						f (1,8)
					2
1,25 5						(0,8			2	1) (1,1			2	1)		(1,4	2		1) (1,8		2	1)
0,3				2
0,3 2,125					1,64 2,21 2,96								3,89 0,3 13,825									4,1475
Погрешность расчета δ I*														I	ТР	4,125 4,1475 0,0225 .

Формула трапеций имеет такую же точность, как и формула центральных прямоугольников.

Знак погрешности легко объяснить по геометрической иллюстрации применения формулы.

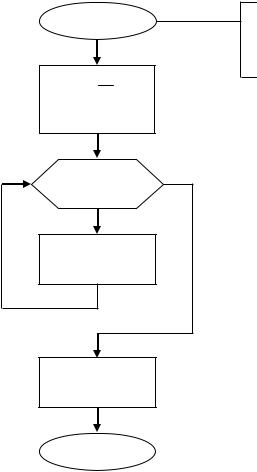
Начало

h bn-a

S f(a) f(b)

2

Входные данные: a – начало отрезка; b – конец отрезка; n – число узлов.

i = 1, n-1, 1

S = S+f(a+i h)

S = h S

Конец

Рис. 28. Блок-схема алгоритма «Метод трапеций»

39