
Численные методы
.pdf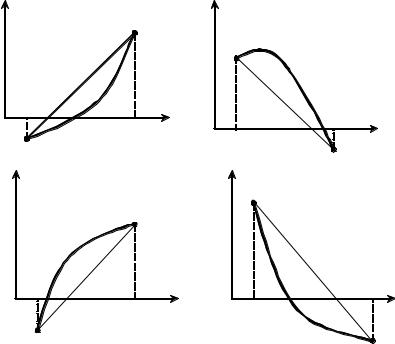
Если x1 оказывается недостаточно точным, находят второе приближение. На основании (6) и (7) соответственно можно записать рекуррентные последовательности:
|
xk 1 xk f (xk ) |
|
b xk |
|
|
, |
|
|
f (b) f (x |
k |
) |
|
|||
|
|
|
|
||||
|
|
|
|
|
|
|
|
если f (xk ) f (b) 0 |
(т.е. корень находится на интервале [xk, b]), и |
||||||
|
xk 1 xk f (xk ) |
xk a |
|
|
|
, |
|
|
f (x ) f (a) |
||||||
|
|
|
|
||||
|
|
|
k |
|
|
|
|
если f (xk ) f (a) 0 |
(т.е. корень находится на интервале [a, xk]). |
||||||
Заметим, что на выделенном интервале [a, b] имеют место четыре типа расположения кривой f(x) (рис 13).
Для I типа о f '(x) > 0, f "(x) > 0, для II типа – f '(x) < 0, f "(x) < 0, для III типа – f'(x)>0, f "(x) < 0; для IV типа – f '(x) < 0, f "(x) > 0.
Тогда для I и для II типов используется (6), т. е. х0 = а. Для III и IV используется (7), т. е. х0 = b.
y |
I |
|
B |
y |
II |
|
|
|
|
|
|
|
|
|
|
|
|
A |
y = f(x) |
|
|
|
|
y = f(x) |
|
|
|
|
|
|
|
|
|
|
a |
x1 |
b |
|
|
b |
|
|
|
x |
|
|
||
A |
|
a |
x1 |
x |
||
|
|
|||||
|
III |
|
|
y |
B |
|
y |
|
|
IV |
|
||
|
|
|
A |
|
||
|
|
|
B |
|
|
|
|
a |
|
|
|
x1 |
b |
A |
x1 |
b |
x |
a |
|
x |
|
|
|
|
|
B |
|
|
|
|
|
|
|
|
|
Рис. 13. Типы кривой для метода хорд |
|
||||
20
|
Начало |
|
|
Ввод a, b, |
|
|
x:=a-f(a)*(b-a)/(f(b)-f(a)) или (11) |
|
Нет |
f(a)∙f(x)≤0 |
Да |
|
|
|
a:=x |
|
b:=x |
|
|f(x)| ≤ |
Нет |
|
|
|
|
Да |
|
|
Вывод x |
|
Конец
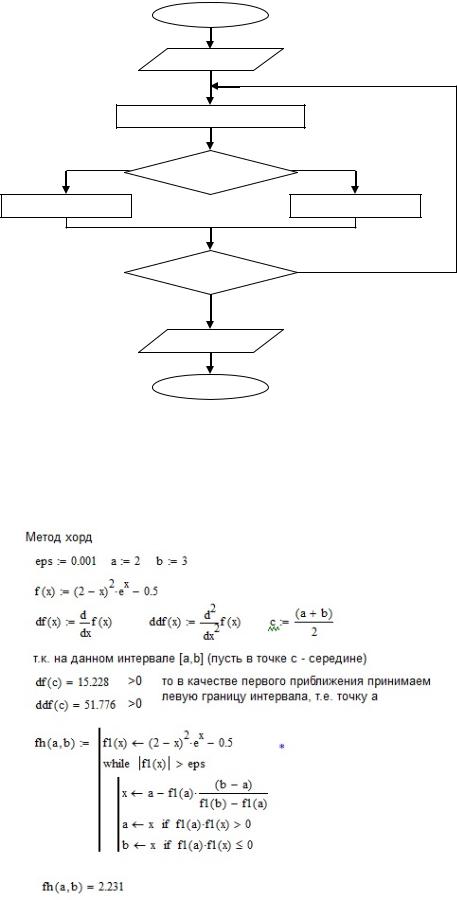
Рис. 14. Блок-схема алгоритма «Метод хорд»
Пример 5. Найдем решение уравнения из примера 1 методом хорд в
Mathcad (рис. 15) и в Pascal ABC (рис. 16).
Рис. 15. Пример реализации «Метод хорд» в Mathcad
21
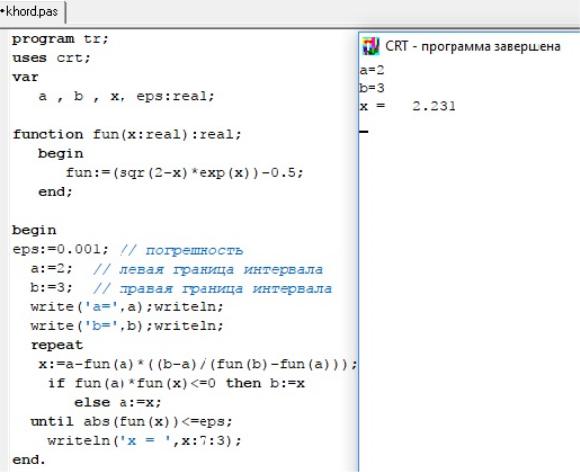
Рис 16. Пример реализации «Метод хорд» в Pascal ABC
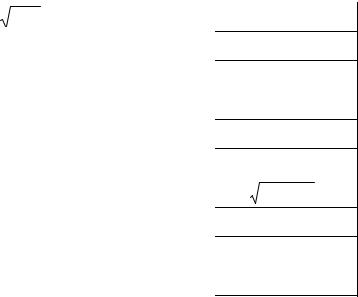
2.4. Индивидуальные задания для лабораторной работы № 1
Найти корни нелинейного уравнения f(x)=0 с помощью приближенных методов по алгоритму:
1.Отделить корни, используя графический и аналитический методы.
2.Используя микрокалькулятор, сделать 3 шага методами: половинного деления, касательных и хорд. Для каждого метода указать приближенное значение корней и погрешность, с которой найден корень.
3.Реализовать данные методы с помощью программирования в Pascal ABC и системе Mathcad.
22
1 |
x cos x 0 |
11 |
x 1 1/x |
21 |
5x 8lnx 8 |
|
2 |
2 lg x x 0 |
12 |
x cos x 0 |
22 |
3x ex 0 |
|
|
|
|
|
|
x(x 1)2 1 |
|
3 |
tg (1,9x) 2,8x 0 |
13 |
3x cosx 1 0 |
23 |
||
|
|
|
|
|
x (x 1)2 |
|
4 |
sin(2,2x) x 0 |
14 |
x3 2x 5 0 |
24 |
||
5 |
ln(8x) 9x 3 |
15 |
x3 2x2 4x 7 0 |
25 |
x2 sinx |
|
6 |
0,7e 0,59x x 0 |
16 |
(2 x)2 0,5e x |
26 |
x3 sinx |
|
7 |
5,6 sin( 4,8x) 4,5x 0 |
17 |
x3 3x 0.4 0 |
27 |
x |
lg(x 2) |
8 |
x4 4x 1 0 |
18 |
2,2x 2x 0 |
28 |
x 2 ln(x 1) |
|
9 |
lnx (x 1)3 0 |
19 |
x2 4sinx 0 |
29 |
2x ln x 0,5 |
|
10 |
x 2x 1 |
20 |
2x ln x 7 |
30 |
2x cos x 0,5 |
|
2.5.Вопросы для самоконтроля
1.Какого типа уравнения решаются в данной работе ?
2.Что называется корнем уравнения f(x) = 0 ?
3.Как графически решить уравнения f(x) = 0, f1(x) = f2(x) ?
4.Перечислите достоинства и недостатки графического метода. В чем состоит этап отделения корней уравнения f(x) = 0?
5.Сколько корней должна иметь функция f(x) на начальном отрезке
[a, b]?
6.Как определить аналитически: возрастает или убывает функция на промежутке?
7.Как определить аналитически: выпукла или вогнута функция на промежутке?
8.Какие условия, наложенные на f(x), гарантируют наличие хотя бы одного корня уравнения на начальном отрезке [a, b]?
9.Какие условия, наложенные на f(x), гарантируют наличие не более одного корня уравнения на начальном отрезке [a, b]?
23
10.Привести алгоритм решения уравнения f(x) = 0 методом половинного деления. Какие условия при этом должны быть наложены на функцию f(x)?
11.Какие условия должны быть наложены на f(x), чтобы уравнение можно было решить методом Ньютона?
12.Как выбирается начальная точка x0 в методе Ньютона?
13.Вывести формулу для вычисления n последовательных приближений методом Ньютона, записать формулу оценки погрешности.
14.Какие условия должны быть наложены на f(x), чтобы уравнение f(x) = 0 можно было решить методом хорд?
15.Как выбирается начальная точка x0 в методе хорд?
16.Вывести формулу для вычисления n последовательных приближений методом хорд, записать формулу оценки погрешности.
24
3. ЛАБОРАТОРНАЯ РАБОТА № 2 ИНТЕРПОЛИРОВАНИЕ ФУНКЦИЙ
3.1. Постановка задачи. Интерполяционная формула Лагранжа
Пусть при изучении некоторого явления установлено, что существует некоторая функциональная зависимость между величинами x и y, описывающая количественную сторону данного явления; при этом функция y = f(x) остается нам неизвестной, но на основании эксперимента установлены значения этой функции y0, y1,…., yn, при некоторых значениях аргумента x0, x1,…., xn принадлежащих отрезку [a,b].
Задача заключается в том, чтобы найти функцию, по возможности более простую с вычислительной точки зрения (например, многочлен), которая представляла бы функцию на отрезке [a, b] точно или приближенно. В более отвлеченной форме эту задачу можно сформулировать так: на отрезке [a, b] заданы значения неизвестной функции y = f(x) в n+1 неизвестных точках x0, x1,…., xn называемых узлами интерполирования: y0 = f(x0), y1 = f(x1), …, yn = f(xn); требуется найти многочлен L(x) наименьшей целой степени, который в узлах интерполирования принимает так же значения yi, i = 1..n, что и функция f(x) , то есть удовлетворят условиям интерполирования:
L(xi ) f (xi ) yi ,i 1..n |
(8) |
В качестве искомого многочлена возьмем многочлен n-ой степени вида:
L(x) C0 (x x1) (x x2 ) ... (x xn ) C1 (x x0 ) (x x2 ) ... (x xn ) (9)C 2 (x x0 ) (x x1) ... (x xn ) ... C n (x x0 ) (x x1) ... (x xn 1)
И определим коэффициенты C0, C1,… Cn, так чтобы выполнялись условия интерполирования (8).
Положим по формуле (9) x = x0, тогда принимая во внимание равенства
(8), получим |
|
y0 C0 |
(x0 |
x1) (x0 |
x2) ... (x0 xn ), |
||||||
Откуда |
C0 |
|
|
|
|
|
y0 |
|
|
, |
|
(x |
x ) (x |
x ) |
... (x |
x ) |
|||||||
|
|
|
|
||||||||
|
|
|
0 |
|
1 |
0 |
2 |
0 |
n |
|
|
25

Затем, положив x=x1, получим y1 C1 (x1 x0) (x1 x2) ... (x1 xn ) ,
Откуда |
C1 |
|
|
|
|
|
|
|
|
y1 |
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
(x |
x ) (x |
x |
) ... (x x |
) |
|
|
|
|
|
|
|
||||||||||||||
|
|
|
1 |
0 |
|
|
|
|
1 |
2 |
|
|
|
1 |
n |
|
|
|
|
|
|
|
|
|
|
Таким же образом найдем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
C2 |
|
|
|
|
|
|
|
|
|
y2 |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
(x |
2 |
x ) (x |
2 |
x ) |
(x |
2 |
x ) ... (x |
x |
) |
|
|||||||||||
|
|
|
|
|
|
|
|
|
0 |
|
|
1 |
|
|
3 |
0 |
|
n |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
… |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Cn |
|
|
|
|
|
|
|
|
|
|
yn |
|
|
|
|
|
|
|
|
|
||
|
|
|
(x |
n |
|
x ) (x |
n |
x ) (x |
n |
x |
) ... (x |
n |
x |
n 1 |
) |
||||||||||
|
|
|
|
|
|
|
|
|
0 |
|
1 |
|
2 |
|
|
|
|||||||||
Подставляя найденные значения коэффициентов Ci в формулу (9), получим:
n |
(x xk ) |
|
|
|
L(x) |
i k |
f (xi ) |
(10) |
|
(xi xk ) |
||||
i 0 |
|
|
i k
Эта формула называется интерполяционной формулой Лагранжа.
Отметим без доказательства, что если функция y = f(x) имеет производную (n+1)-го порядка на отрезке [a, b], то погрешность при замене функции f(x) многочленом L(x) удовлетворяет неравенству
f (x) L(x) |
|
|
M n 1 |
|
(b a)n 1, где M n 1 max |
|
f n 1(x) |
|
x [a,b]. |
|
|
|
|
||||||
|
|||||||||
|
(n 1)! |
||||||||
|
|
|
|
|
|
|
|
||
Пример 6. Из эксперимента получены значения функции y = f(x): y0 = 3 при x0=1, y1=-5 при x1=2, y2 =4 при x2 = 3. Требуется представить приближенную функцию y = f(x) многочленом Лагранжа 2-й степени.
По формуле (10) имеем (при n=2):
L(x) |
(x |
2) |
(x 3) |
3 |
(x |
1) |
(x 3) |
( 5) |
(x |
1) |
(x 2) |
4, отсюда: |
|
(1 |
2) |
(1 3) |
(2 |
1) |
(2 3) |
(3 |
1) |
(3 2) |
|||||
|
|
|
|
L(x) 172 x2 672 x 28.
Покажем решение данной задачи в Mathcad:
26
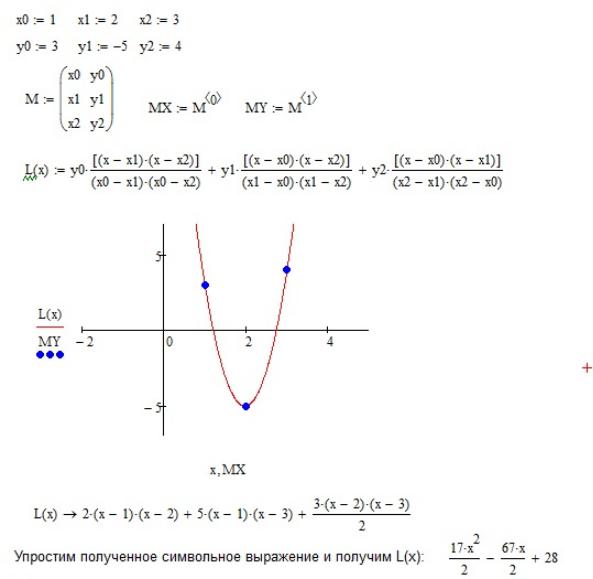
Рис. 17. Пример нахождения интерполяционного многочлена Лагранжа в Mathcad
3.2. Интерполяционный многочлен Ньютона
Существуют и другие интерполяционные функции. Одна из них – интерполяционная формула Ньютона.
Пусть известны (n+1) значений функции y = f(x), а именно y0 = f(x0), y1 = f(x1), …, yn = f(xn) при n+1 значений аргумента x0, x1,…., xn. При этом разность между соседними аргументами постоянна. Обозначим ее через h. Таким образом, имеем следующее значение аргумента:
x0, x1=x0+h, x2=x0+2∙h, …, xn=x0+n h.
27

Составим многочлен степени не выше n, который принимает соответствующие значения при соответствующих значения x. Этот многочлен будет приближенно представлять функцию f(x).
Предварительно введем обозначения:
y0 y1 y0, y1 y2 y1, y2 y3 y2, y3 y4 y3, ...,2 y0 y1 y0, 2 y1 y2 y1, 2 y2 y3 y2, ...,
3y0 2 y1 2 y0, 3y1 2 y2 2 y1, ...,
………………………………..
n y0 n 1y1 n 1y0
Это так называемые разности 1-го, 2-го,…, n-го порядка.
Напишем многочлен, принимающий значения y0, y1 соответственно при x0, x1. Это будет многочлен первой степени
N1(x) y0 y0 x hx0 .
Многочлен принимающий значения y0, y1, y2, соответственно при x0, x1, x2 – это многочлен второй степени.
N 2(x) y0 y0 x hx0 22y!0 x hx0 (x hx0 1).
Многочлен третьего порядка будет иметь вид:
N 3(x) y0 y0 x hx0 22y!0 x hx0 (x hx0 1) 33y!0 x hx0 (x hx0 1) (x hx0 2)
Наконец, многочлен n-го порядка будет иметь вид:
N n(x) y0 y0 |
|
x x0 |
|
2 y0 |
|
x x0 |
( |
x x0 |
1) ... |
|
||||||||
|
2! |
|
|
h |
(11) |
|||||||||||||
|
n y0 |
|
|
|
|
|
h |
|
|
|
|
h |
|
|
|
|||
|
|
x x0 |
( |
x x0 |
1) ... ( |
x x0 |
(n 1)) |
|
|
|||||||||
h |
|
|
|
|
||||||||||||||
|
n! |
|
|
|
|
h |
|
|
|
|
|
h |
|
|
|
|
|
|
В чем можно убедиться непосредственной подстановкой. Это и есть
интерполяционный многочлен Ньютона.
По существу, многочлен Лагранжа многочлен Ньютона для данной таблицы значений тождественны, но по-разному написаны, так как многочлен степени не выше n, принимающий заданные n+1 значений при данных n+1 значениях x, находится единственным образом.
28
Во многих случаях интерполяционный многочлен Ньютона более удобен, чем интерполяционный многочлен Лагранжа. Особенность этого многочлена заключается в том, что при переходе от многочлена k-ой степени к многочлену (k+1)-ой степени первые k+1 членов не меняются, а только добавляется новый член, который равен нулю при всех предыдущих значениях аргумента.
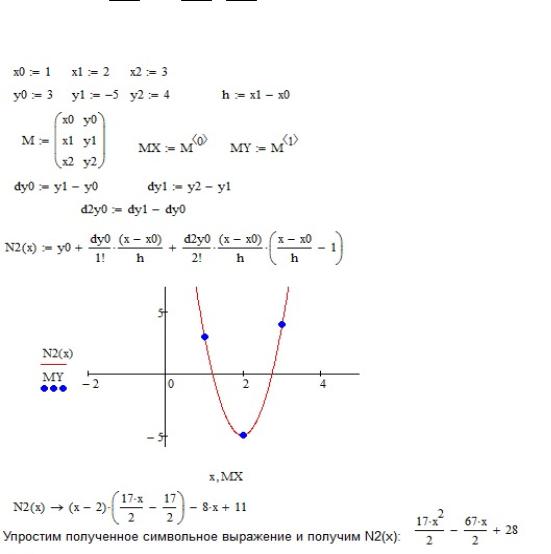
Пример 7. Представим приближенную функцию y= f(x) из примера 6 многочленом Ньютона 2-й степени.
Вычислим разности первого и второго порядков:
y |
0 |
5 3 8, y 4 ( 5) 9, 2 y |
0 |
y y |
0 |
9 ( 8) 17. |
|
1 |
1 |
|
Теперь по формуле (11) при n = 2, h = 1 имеем:
N (x) 3 ( 8) x 1 1 172! x 1 1 (x 1 1 1), отсюда N (x) 172 x2 672 x 28.
Покажем реализацию данного алгоритма в Mathcad:
Рис. 18. Пример нахождения интерполяционного многочлена Лагранжа в Mathcad
29
