Численные методы

Рис. 29. Пример реализации метода прямоугольников в Pascal ABC

Рис. 30. Пример реализации метода трапеций в Mathcad 40

4.4. Формула Симпсона

На каждом элементарном отрезке подынтегральная функция f(x) заменяется квадратичной параболой, построенной по трем точкам: концам эле-

ментарного отрезка (xi,fi ), ( xi 1,fi 1) и его середине ( xi h2 ,~fi ).

Площадь полученной криволинейной трапеции служит оценкой элементарной площади Si:

Si h6 fi 4~fi fi 1 h6 f (xi ) 4f (xi h2) f (xi 1) .

Тогда значение интеграла:

n 1 h

I* i 0 6 fi 4fi fi 1

h6 f0 4f0 f1 f1 4f1 f2 ... fn 2 4fn 2 fn 1 fn 1 4fn 1 fn .

Добавим в скобки

f0 f0 , вынесем общий множитель за скобки:

h

f

n

f

0

n 1

~

h

f (b) f (a)

n 1

h

I *

f

2 f

f (a ih) 2 f (a ih

)

i

3

2

i

3

2

2

i 0

i 0

.

Формула Симпсона имеет высокую точность, так как погрешность метода м = О(h3)

Пример 10. Вычисление значения ранее рассмотренного интеграла I 0,52 x2 1 dx по формуле Симпсона:

Для упрощения расчета возьмем n =2, тогда h = 0,75.

f (b)

f (a)

n 1

h

I

c

h

( f (a

i h) 2

f (a i h

))

2

2

i 0

0,75

f( 2)

f( 0,5)

1

( f (0,5

i 0,75)

2 f (0,5 i 0,75 0,375))

3

2

i 0

41

	1				(2	2	1)	2	1)
								(0,5		f	(0,5) 2	f (0,875) f (1,		25)
	4							2							2 f (1,625)
	1				5 1,25			2	1) 2		2	2		2	2	1)
	4					2		(0,5			(0,875	1) (1,25	1)		(1,625
	1		1,875 1,25 3,53125								2,5625 7,28125		16,5	4,125.
	4												4

Погрешность расчета = 4,125 – 4,125 = 0.

Такой результат объясняется тем, что подынтегральная функция в примере является квадратичной параболой, и замена ее параболой не вносит погрешности метода, а погрешность округления в расчётах отсутствует.

Рассмотренные формулы являются частным случаем формулы НьютонаКотеса, полученной в общем виде при замене подынтегральной функции f(x) полиномом k-ой степени (при k = 1 – формула трапеций, при k = 2 –

формула Симпсона). Чем больше k, тем точнее вычисляется интеграл при одинаковом числе узлов n.

Начало

h bn-a

S f(b) f(a)

2

i = 0, n-1, 1

S = S+f(a+i h)+ +2 f(a+i h+h/2)

S13 h S

Конец

Входные данные: a – начало отрезка; b – конец отрезка; n – число узлов.

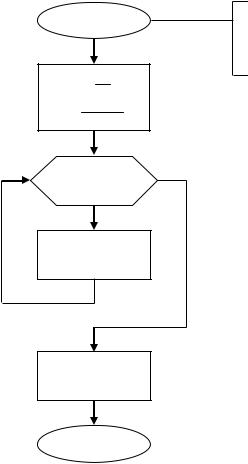
Рис. 31. Блок-схема алгоритма «Метод Симпсона»

42

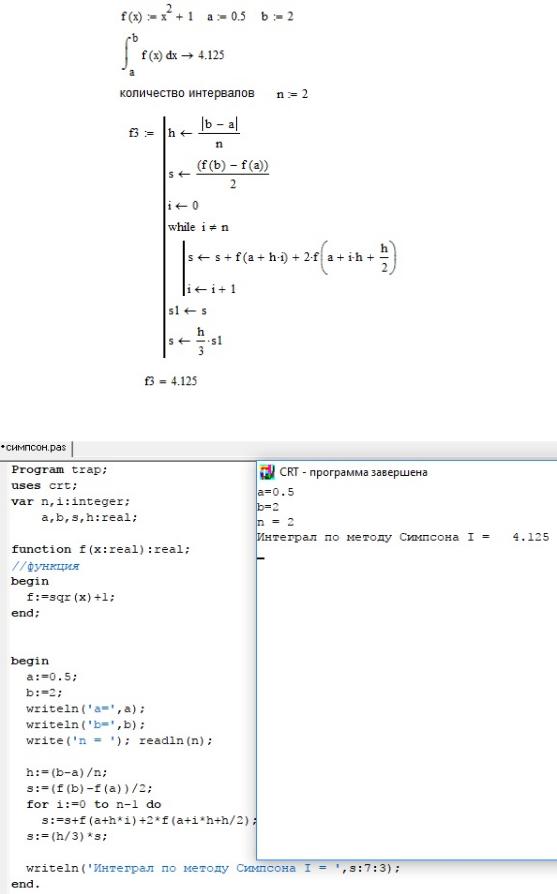
Рис. 32. Пример реализации метода Симпсона в Mathcad

Рис. 33. Пример реализации метода Симпсона в Pascal ABC 43

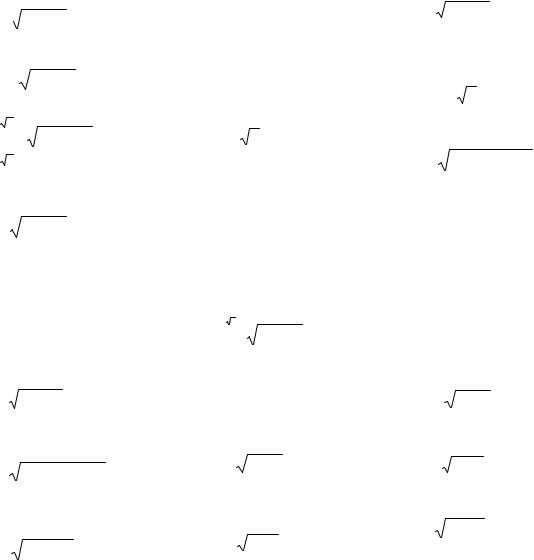
4.5. Индивидуальные задания для лабораторной работы № 3

Вычислить определенные интегралы с помощью приближенных методов по алгоритму:

1.Вычислить интеграл аналитически.

2.Используя микрокалькулятор, сделать три шага методами: прямоугольников, трапеций и Симпсона. Для каждого метода указать приближенное значение корней и погрешность, с которой найден корень.

3.Реализовать данные методы с помощью программирования в Pascal ABC и системе Mathcad.

4.Сравнить точность полученных результатов. Сделать выводы.

		e				dx						1				arctgx
																													4			dx
1											11														dx			21
				x(1 ln			2		x)							1				x		2
																														1	sin				2		x
	1											0																	0
	14																												e		1 ln x
																			etg 3x
						2x 1dx						12
2		3									12																dx	22										dx
																					2
	1																cos							3x					1			x
												0
3	2										13					1			dx									23	1		xdx
	x 4 x2dx											e x2
												2
																													0 1				x
	0											1					x
4			2								14								x dx									24				2				dx
		x 2x2 3dx
												1																	0
													0																2		x 2x 9
			6												1 x
		2
	1					3x3dx																							3				dx
												2
5											15		sin							3		xdx						25
			5			2 x4																								x	2	4x 5
	0																												2
												0
												1					xdx												e2		dx
6	2										16																	26
		esin3x cos3xdx
																							2
																														x ln x
	0												0 1 x																e
				2x cosx								5										2							1	ex dx
7				x2 sin x dx							17		x							x					4dx			27
																														1	e		2x
	2											0																	0
	1																												9
													2 cos3 xdx																			1 xdx
8		3				2 e3x e3x dx					18																	28	x3
	0											0																	1
												5																	5
	4																	x 1dx
9						3 4cos2x sin2xdx					19																	29	x x 4dx
												1																	0
	0
	1											4						xdx											2
		6 arcsin3xdx
10											20																	30			4 x2 dx
	0					1 9x2						1						x 5											2

44

4.6.Вопросы для самоконтроля

1.Дайте определение определенного интеграла.

2.Дайте определение неопределенного интеграла.

3.Что такое первообразная для функции?

4.Приведите формулу Ньютона-Лейбница.

5.В каких случаях целесообразно использовать формулы численного интегрирования?

6.Используя геометрическую интерпретацию, выведите формулы левых и правых прямоугольников.

7.Приведите оценку погрешности формул левых и правых прямоугольников.

8.Выведите формулу средних прямоугольников.

9.Приведите оценку погрешности формулы средних прямоугольников.

10.Выведите формулу трапеций.

11.Приведите оценку погрешности формулы трапеций.

12.Выведите формулу Симпсона.

13.Приведите оценку погрешности формулы Симпсона.

14.Получите формулу выбора начального шага в формуле трапеций.

15.Получите формулу выбора начального шага в формуле Симпсона.

16.В чем состоит правило Рунге оценки погрешностей? Получите оценки погрешностей формул трапеций и Симпсона по правилу Рунге.

17.Как находится полная погрешность вычисления определенного интеграла?

45

5. ЛАБОРАТОРНАЯ РАБОТА № 4 ЧИСЛЕННЫЕ МЕТОДЫ РЕШЕНИЯ ОБЫКНОВЕННЫХ

ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ

5.1. Постановка задачи

Приемы нахождения решений дифференциальных уравнение через элементарные (или специальные) функции, разработанные в классическом анализе, часто оказываются неприменимыми. Поэтому для решения практических задач созданы методы приближенного решения дифференциальных уравнений. Эти методы подразделяются на три основные группы:

1.Аналитические методы, применение которых дает решение дифференциального уравнения в виде аналитического выражения.

2.Графические методы, когда искомая функция получается в виде графика.

3.Численные методы, когда искомая функция получается в виде таблицы.

Ниже рассматриваются относящиеся к указанным группам некоторые методы решения обыкновенных дифференциальных уравнений.

5.2.Метод Эйлера

Воснове метода Эйлера лежит идея графического построения решения дифференциального уравнения. Однако этот метод дает одновременно и способ нахождения искомой функции в численной (табличной) форме.

Дифференциальное уравнение y f (x,y)определяет на плоскости поле направлений, т. е. в каждой точке плоскости, в которой существует функция f (x,y), уравнение задает направление интегральной кривой уравнения, проходящей через эту точку. Пусть требуется решить задачу Коши: найти решение уравнения y f (x,y), удовлетворяющее начальным усло-

виям y(x0) y0. Разделим отрезок x0,xn на n равных частей и положим,

46

	что	h	xn x0	(h – шаг изменения аргумента). Внутри элементарного
			n

промежутка от х0 до х0+h заменим функцию y на ∆y/∆x, т.е. на (yi – yi-1) / h.

Тогда y1 y0 h f (x0,y0), где у1 – значения искомой функции, соответ-

ствующее значению х1 = х0+h. Отсюда получаем y1 y0 h f (x0,y0). Повторяя эту операцию, получим последовательные значения функции:

y2 y1 h f (x1,y1); y3 y2 h f (x2,y2);

……………………;

yk 1 yk h f (xk ,yk ).

Таким образом, можно приближенно построить интегральную кривую в виде ломаной с вершинами Mk (xk, yk ), где, хk+1 = хk+h

yk 1 yk h f (xk ,yk ).

Начало x0, h, y0, n

i = 1

y = y0 + h f(x, y0)

x = x + h

Вывод x, y

i < n	Да	y0 = y
		i = i + 1

Нет

Конец

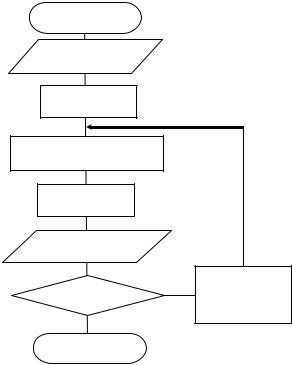
Рис. 34. Блок-схема алгоритма «Метод Эйлера»

47

Пример 11. Решите методом Эйлера дифференциальное уравнение

y y x с начальным условием у(0) = 1, приняв шаг h = 0,1. y x

Ограничимся нахождением первых четырех значений у. Находим последовательные значения аргумента х0 = 0, х1 = 0,1, х2 = 0,2,

х3 = 0,3. Вычислим соответствующие значения искомой функции: y1 y0 h f (x0,y0) 1 0,1 11 00 1,1;

y2 y1 h f (x1, y1) 1,1 0,1 1,11,1 0,10,1 1,183;

y3 y2 h f (x2, y2 ) 1,183 0,1 1,183 0,2 1,254; 1,183 0,2

y4 y3 h f (x3, y3) 1,254 0,1 1,254 0,3 1,315. 1,254 0,3

Составим таблицу, приведя результат с двумя знаками после запятой:

х	0	0,1	0,2	0,3	0,4
у	1	1,1	1,18	1,25	1,31

Рассмотрим решение данного примера в Mathcad:

Рис. 35. Пример реализации метода Эйлера в Mathcad

48

		5.3. Метод Рунге – Кутта
	Пусть функция у определяется дифференциальным уравнением
	f (x,y)	при начальном условии y(x0) y0. Приведем без вывода один
y

из вариантов соответствующих расчетных формул. При численном интегрировании дифференциального уравнения методом Рунге – Кутта определяют четыре числа:

k h f (x,y);

k

2

h f (x h ,y k1 );

1

2

2

k h f (x h

,y k2 );

k h f (x h,y k ).

3

2

2

4

3

1 k1

Если положить y y(x h) y(x),

то у

2k2 2k3 k4 (при-

6

нимаем без доказательства). Схема вычислений имеет вид:

х

у

k f h f (x,y)

х0

у0

k1

у

1

2k3

k4

6 k1 2k2

x0

h

y0

k1

k

2

2

2

x0

h

y0

k2

k

2

2

3

x0 h

y0 k3

k4

x1 x0 h

y1 y0 k

Отметим, что в этом случае погрешность на каждом шаге пропорциональна пятой степени шага h 5 . Отсюда, в частности, следует, что при до-

статочно малом h и малых погрешностях вычислений решение уравнения y f (x,y), полученноеметодом Рунге–Кутта,будетблизкимк точному.

Пример 11. Решите методом Рунге – Кутта дифференциальное уравнение x2 y xy 1 с начальным условием у(1) = 0 на отрезке [1, 2], положив

шаг h равным 0,2 [точное решение y x22x 1].

49