2.8Факторизация.

Пусть теперь t - некоторая (конечная или бесконечная) совокупность подмножеств В_i множества А. Таким образом, элементами t являются подмножества В_i множества А. Говорят, что t задает разбиение множества А, если объединение всех элементов t равно А, а любые два элемента В_i¹В_j при этом не пересекаются (как подмножества А). Иными словами, все элементы разбиения - подмножества множества А - взаимно не пересекаются и каждый элемент множества А принадлежит какому-то элементу разбиения: 1)A= и 2)(В_i.¹В_j)Þ (В_i.ÇВ_j =Æ).

Упражнение 7.

Перед вами три рисунка. На одном из них изображено разбиение. На котором? И почему не годятся два остальных?

Примеры разбиений:

1. единственным элементом разбиения является само множество А;

2. элементами разбиения являются сами элементы множества А (каждый элемент А рассматривается как его одноточечное подмножество);

3. разбиение, состоящее из двух элементов: собственного подмножества множества А и его дополнения.

Упражнение 8.

Каждое отношение эквивалентности на множестве А определяет разбиение этого множества (на классы эквивалентности) и, наоборот, каждое разбиение множества А задает на нем отношение эквивалентности.

Def³. Множество, элементами которого являются классы эквивалентности (или, что то же самое, элементы разбиения) называется фактор-множеством. Любой элемент из класса эквивалентности называется его представителем. Множество, состоящее из представителей, выбранных по одному от каждого класса, называется системой представителей (соответствующей данному разбиению).

Примеры.

Будем считать двух учеников школы эквивалентными, если они учатся в одном классе. Тогда множество классов этой школы будет фактор-множеством множества учеников по данному разбиению (отношению эквивалентности). Если выбрать из каждого класса по одному ученику, то эти ученики составят множество представителей этих классов.

Так же можно разбить и множество всех людей на нашей планете по отношению эквивалентности: два человека эквивалентны, если они проживают в одной стране.

Тогда фактор-множеством станет множество всех стран на Земле, и, если выбрать по представителю от каждой страны, то они составят систему представителей.

Процедура перехода от самого множества к его фактор-множеству называется факторизацией (по данному разбиению или отношению эквивалентности).

Она проходит красной нитью через всю математику и от того, как вы её усвоите, в значительной степени зависит то, как вы усвоите всё остальное.

А прямо сейчас нам предстоит встретиться с этой процедурой при построении отрицательных чисел – расширении натуральных чисел до целых.

3Построение z.

Р ассмотрим сначала такой пример. Число 2 является решением уравнения 1+х=3. Можно сказать, что пара чисел (3,1) определяет число 2. Отметим эту пару точкой A на «четвертинке» плоскости NN, называемой первым квадрантом. Но разве только решением уравнения с такими именно числами является 2? А если добавить к обеим частям равенства одно и то же число, равенство же останется в силе: 2+х=4; 3+х=5, 4+х=6,…Стало быть, все эти пары чисел, (4,2); (5,3); (6,4) определяют таким же образом одно и то же число 2. Отметим их все в том же произведении натуральных чисел на себя. Получилась бесконечная цепочка точек, лежащая на луче, исходящим из точки А(3,1) и уходящим в бесконечность параллельно прямой у=х.. Назовём все эти точки эквивалентными и представляющими число 2. Любую из них можно взять в качестве представителя числа 2, а само число 2 – это все эти точки, весь этот «луч».

Повторим теперь эту процедуру с произвольным числом.

Пусть даны натуральные числа а и b. Рассмотрим опять уравнение а+х=b.

Пока мы находимся в области натуральных чисел, решение (это и есть, по определению, разность b и а, а процедура нахождения этого решения называется вычитанием а из b) существует (и единственно) только при a<b. Кроме того, мы знаем, что число х даже при a<b не определяет эту пару (b,a) однозначно. Если мы прибавим любое натуральное число с к обеим частям уравнения, то от этого его решение не изменится: а+с+х= b+с.

Отметим точку (b,a). Все точки с координатами (b+c, a+c) определяют одно и то же число х. Поэтому мы их все и отметим. Все эти точки с натуральными координатами лежат на одном луче, выходящим из точки (b-a+1,1). Все они, вместе взятые, целиком и определяют число х – решение исходного уравнения. Другие лучи определяют другие числа.

Все эти лучи параллельны друг другу и лучу у=х и выходят из точек со второй координатой, равной единице. Все получающиеся таким образом лучи образуют пучок параллельных лучей, лежащих в правой нижней половине квадранта (снизу от биссектрисы прямого угла). На рисунке внизу они отмечены фиолетовым цветом.

Назовём эти лучи числами.

Научимся теперь складывать числа-лучи. Пусть у нас имеются два луча, m и n.

Возьмём на каждом из двух лучей по точке-представителю: (а,b) из m и (c,d).из n. Сложим их покомпонентно⁴ и рассмотрим луч, проходящий через полученную точку (a+c, b+d). Его мы и назовём суммой лучей (чисел!) m и n. Надо ещё проверить корректность этого определения, а именно, что эта сумма (луч) не будет зависеть от того, какие именно точки мы взяли на исходных слагаемых-лучах m и n в качестве представителей.

Упражнение 9. Убедитесь в этом. Возьмите другие точки на тех же самых лучах и покажите, что полученная вами в результате сложения точка принадлежит тому же лучу.

Упражнение 10. Какой луч будет играть роль «нуля»: его прибавление к любому лучу, оставляет этот луч на месте?

Упражнение 11. Какую точку надо прибавить к (а,b) чтобы получилась точка на нулевом луче?

Последнее упражнение и позволило нам определить отрицательные числа. Это те числа-лучи, сумма которых с положительными лучами равна нулю.

У отрицательных лучей, как легко видеть, первая координата больше второй.

Где проходят положительные лучи? Где проходят отрицательные лучи?

Лучи, сумма которых равняется нулевому лучу, называются взаимно противоположными. Как взаимно противоположные лучи расположены относительно друг друга?

Обратите внимание на следующие важные обстоятельства (вы должны уметь их обосновать).

• Через каждую точку первого квадранта NN целочисленной плоскости проходит один и только один луч. Таким образом, возникло разбиение множества точек NN на лучи.

• Каждому лучу соответствует и при том однозначным образом противоположный ему луч, т.е. луч, сумма с которым равняется нулевому лучу.

Осталось определить умножение чисел-лучей.

Опять возьмём представителей (а,b) и (c,d) лучей m и n.

Найдём точку с координатами (ac+bd, ad+bc) и проведём через неё луч, параллельный всем остальным лучам в нашем множестве лучей. Его мы и назовём произведением лучей m и n.

Упражнение 12*. Проверьте, что и это определение корректно.

Def⁵. Построенное нами множество чисел-лучей вместе с введёнными над ними операциями сложения и умножения называется кольцом⁶ целых чисел. Оно обозначается буквой Z.

Н апомню, что коммутативность a+b=b+a и ассоциативность (a+b)+c=a+(b+c) операции сложения натуральных чисел усматривается непосредственно, если представлять себе, что мы складываем вместе какие-либо предметы. С теми же свойствами умножения дело обстоит чуточку сложнее. Для того, чтобы представить себе получающуюся геометрическую картинку, рассмотрим пример. Пусть мы умножаем два на три. Это значит, складываем три два раза: 23=3+3. Возьмём одну тройку камешек или фишек и поставим вторую тройку рядом, напротив первой:

Е сли мы расположим каждый ряд из трёх фишек в линию на одном и том же расстоянии друг от друга и точно под первым рядом расположим второй, то все вместе 6 фишек образуют прямоугольник размером как раз 23.

Теперь если нам нужно поменять сомножители местами, три раза сложить два, то нам достаточно просто повернуть этот же прямоугольник (или свою голову).

32=2+2+2. Ясно, что количество фишек при этом не изменится.

В общем виде это выглядит, как ab=ba, где a и b – натуральные числа.

Д ля объяснения ассоциативности используем не круглые плоские фишки, а кубики. Представим себе, что мы умножаем двумя способами 3, 5 и 6. По первому способу сначала умножаем 3 на 5, а потом результат умножаем на 6. По второму сначала умножаем 5 на 6, а затем результат (произведение 5 и 6) умножаем на 3. Предположим, что у нас имеются кубики 111м и комната с размерами 5м в ширину, 6м в длину и 3м в высоту.

(35)6: выкладываем заднюю стенку высотой 3м во всю ширину (5м) комнаты:

На эту стенку как раз и уйдут 35 кубиков. Теперь, если мы поставим рядом 6 таких стенок, то они как раз и заполнят всю комнату.

Если же выложить в один ряд пол, то на это уйдёт 56 кубиков. Если поставим на этот пол ещё два таких же, то мы опять заполним ту же самую комнату, на этот раз, двигаясь снизу вверх.

В итоге и получим, что (35)6=3(56).

В общем виде это выглядит, как a(bc)=(ab) c, где a, b и c – натуральные числа.

Осталось у нас ещё одно свойство, связывающее сложение и умножение – дистрибутивность. Его тоже можно обосновать геометрически. Допустим, нам нужно умножить 3 на 4, потом 3 на 5 и оба произведения сложить. Строим два прямоугольника 34 и 35 и прикладываем их друг к другу по общей стороне 3:

Видно, что получается один большой прямоугольник со сторонами 3 и (4+5). Поэтому и выполняется 34+35=3(4+5). В общем виде это выглядит, как a(b+c)=ab+ac, где a, b и c – натуральные числа.

Обратите внимание, что эти же законы выполняются для операций над высказываниями и над множествами. Но разница все-таки есть.

Упражнение 13. В чём же она?

Упражнение 14. Исходя из того, что для натуральных чисел выполняются обычные законы арифметики (коммутативность, ассоциативность и дистрибутивность) докажите, что эти же законы выполняются и для определённых выше действий с целыми числами (лучами l,m, n). Определим теперь порядок на множестве целых чисел. Обозначим луч, содержащий точку (а,b) как [a,b]. Считаем, что число [а,b]>0 если а>b. (Напомним, что а и b – натуральные числа, для них это понятие уже введено).

Упражнение 15. Докажите, что это определение корректно (т.е., не зависит от выбора точки-представителя).

Вычитание определим, как и раньше: разностью m-n чисел-лучей m и n называется число-луч, являющееся решением уравнения n+x=m.

Упражнение 16. Докажите корректность этого определения.

Теперь распространим отношение порядка на все целые числа.

Будем считать, что m>n если m-n>0.

Упражнение 17. Проверьте корректность этого определения.

Упражнение 18.

Докажите, что отношение порядка линейно, то есть, для любых двух целых чисел m, n выполняется одно и только одно утверждение: m>n, n>m или m=n.

Упражнение 19.

Докажите что отношение порядка транзитивно, т.е. если а>b и b>c, то a>c

Упражнение 20.

Докажите, что отношение порядка и арифметические операции согласованы:

m>n aZ m+a>n+a; m>n aZa>0 ma>na; m>n -n>-m.

Проверьте, что, однако, если a<0, то ma<na. Таким образом, умножение на отрицательное число переворачивает знак неравенства.

На каждом луче, однако, есть среди всех точек, его представляющих, одна особая: его начало (называют её ещё вершиной). Выберем их в качестве представителей и распрямим получившийся прямой угол, повернув луч, смотрящий вверх на 90, так, что он станет вместе с горизонтальным лучом образовывать прямую линию:

П олученная прямая линия из точек называется целочисленной числовой прямой, «посередине» на ней расположена точка «ноль», справа от неё идут целые положительные (натуральные) числа, слева – отрицательные. Возрастают числа слева направо.

Е сли мы возьмём вторую точно такую же целочисленную числовую прямую и поставим её перпендикулярно первой, совместив нули на обеих прямых и направив положительную ось (луч) вверх, то получим целочисленную декартову плоскость – произведение ZZ=Z². Вот что получится:

Горизонтальную числовую прямую называют осью абсцисс, вертикальную – осью ординат. По первой обычно откладывают значения независимой переменной х, по второй – значения функции у=f(x). Примеры функций: a) у=х; b) y=x+1; c) y=x-1; d) y=2x+1; e) y=2x-1.

Часто функции задаются в табличной форме: в верхней строчке пишут значения аргумента, в нижней – значения функции. Вот как выглядит эта таблица для функции у=х:

Х	-2	-1	0	1	2	3	4
У	-2	-1	0	1	2	3	4

Упражнение 21.

Составьте таблицы для остальных функций b) – e) и нанесите на координатную целочисленную плоскость графики соответствующих функций – точки (Х,У) с этими значениями координат (взятыми из соответствующих таблиц).

Делая это упражнение, вы пользовались тем, что, например, 2(-1)=-2. Вообще-то говоря, мы это ещё не доказали, хотя выглядит правдоподобно. Существует несколько объяснений этому, в зависимости от возраста того, кому объясняют – и в каждом из этих объяснений есть доля истины. Например, второклассникам я объясняю это так. Рассмотрим мир стрелок, растущих из ноля и оканчивающихся в натуральном числе. Стрелки можно складывать: не меняя их длины и направления, прикладывать начало одной к концу другой. Получится новая стрелка с началом опять в точке ноль. Пусть, к примеру, мы хотим сложить 1+1. Мы стрелку с началом в нуле и концом в 1 переносим и прикладываем началом к старому экземпляру её самой - стрелке с началом в нуле и концом в 1. Получилась стрелка с концом в 2. Мы просто сделали два шага вправо. Так же мы бы поступили, сложив 2+2. Стрелку 02 приложили бы началом к своему концу и получили бы стрелку 04. Мы сделали два шага вправо, каждый шаг д линой в два единичных отрезка. А теперь повернём влево: для того, чтобы отнять от 4 единицу, нужно к концу стрелки 04 приложить стрелку длиной 1, но смотрящую влево. Она должна, стало быть, торчать из ноля и смотреть в другую с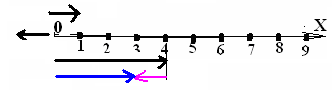 торону. Приложим её так же, как и раньше началом к концу, и она укажет своим концом на 3=4-1. А куда упирается своим концом та повёрнутая стрелка, торчащая из ноля? В место, где должно быть (0-1). Сотрём ноль и о ставим -1. Тогда, если её сложить по нашим правилам с ней же самой, то она удвоится, но будет смотреть в ту же сторону. Итак, гуляя по прямой вправо-влево, мы видим, что отнять 2 от 5 это значит сделать от нуля пять шагов вправо, а потом два влево. Или, наоборот, сначала два шага налево, потом пять направо. То же получится, если приставлять к стрелке «5» стрелку «-2». Или в обратном порядке. То, что я сейчас вам сказал равносильно следующим арифметическим тождествам: (5-2)=-2+5=5+(-2).

Но что такое 2(-1)? Это (-1)+(-1), два шага налево. Разумеется, попадём в -2.

	+	-
+	+	-
-	-	?

Н у, а (-1)2=2(-1) по коммутативности. Итак, «плюс»  «плюс» = «плюс» - это мы знали ещё по натуральным числам в начальной школе; «плюс» «минус» = «минус» «плюс» = «минус», как мы только что выяснили. Осталось заполнить последнюю клеточку в таблице из четырёх возможных вариантов. Если поставить «минус», то у нас окажется один плюс и три минуса. А если «плюс», то плюсов и минусов будет поровну. По справедливости, должен стоять плюс!

Х	4	3	2	1	0	-1	-2
У=-Х	-4	-3	-2	-1	0
У=-2Х	-8	-6	-4	-2	0

Таково моё объяснение второклассникам – и их оно вполне удовлетворяет. Вас, возможно, не вполне. И потому дам вам ещё одно обоснование.

Вы уже построили графики функций у=х и у=2х. Можете построить ещё и график функции у=3х – во всех случаях точки ваших графиков будут лежать на прямых линиях, проходящих через 0. А постройте-ка теперь график функций у=-х и у=-2х. Пока х будет принимать значения 4, 3, 2, 1, 0 – всё хорошо и понятно, положительное число умножается на отрицательное, а это мы уже проходили. Заметим, однако, что на обоих графиках точки снова ложатся на прямые линии!

Чтобы они не сломались, а продолжились во второй квадрант (из четвёртого) как прямые линии, должно быть

–(-1)=1, -(-2)=2; (-2)(-1)=2, (-2)(-2)=4 и т.д.

И вообще, если мысленно представлять себе вертикальную ось как зеркало, то операция умножения на (-1) проявляется как отражение относительно этой оси. Второй раз умножим – опять отразимся и вернёмся назад. Убедил?

Надеюсь, что да. Ученики должны доверять своему учителю. Но если всё-таки остались у вас какие-то сомнения… - тогда докажем этот факт «по-взрослому»!

Вначале докажем, что 0а=0 а. Это можно было бы сделать непосредственно, исходя из нашего определения умножения лучей, но уж раз мы делаем всё по-взрослому, то сделаем по-другому.

Ведь взрослые любят усложнять простые вещи.

Упражнение 22.

Но вы-то пока ещё не взрослые – так что проверьте-ка это правило непосредственно, исходя из нашего определения. А заодно и другое правило: 1а = а а. В качестве представителя 1 выберите чего-нибудь попроще, например, точку (2,1).

Вот именно это, второе правило, мы и используем для вывода правила

«минус»«минус»=«плюс». Но вначале сведём воедино всё, что мы знаем о свойствах операций с целыми числами – лучами.

1. Коммутативность: a+b=b+a; ab=ba)

2. Ассоциативность: (a+b)+c=a+(b+c); (ab)c=a(bc)

3. Дистрибутивность: (a+b)c=ac+bc

4. Наличие нуля: 0| a a+0=a

5. Наличие у каждого элемента a противоположного ему элемента b (обозначаемого как –a) такого, что a+b=0.

6. Наличие единицы: 1| a a1=a

Упражнение 23⁷.

Докажите единственность нуля и единицы. (Hint: assume the opposite)

Упражнение 24.

Докажите единственность противоположного элемента.

Теперь докажем, что умножение на ноль делает произведение равным нулю.

Это непростая задача, и потому дадим к ней указание. Поскольку вы уже доказали единственность нуля, то, обнаружив, что какое-то число в отношении другого числа ведёт себя как ноль, мы можем придти к выводу, что оно и есть ноль: a+x=ax=0.

Упражнение 25*.

Докажите, что a a0=0. (Hint: consider a0+a and use VI and III)

Теперь перед вами открывается возможность доказательства «по-взрослому», что (-a)b=-(ab).

Упражнение 26*.

Воспользуйтесь этой возможностью и докажите это. (Hint: use 15, III and 17)

Если мы перемножим два отрицательных числа, например, -5 и -7, то увидим, что результат зависит только от умножения минус единиц:

(-5)(-7)=(-(15))(-(17))=((-1)5)((-1)7)=(-1)(-1)57.

Итак, всё свелось к вопросу - чему же равно произведение (-1)(-1)?

У нас, судя по предыдущим рассуждениям, есть серьезные основания предполагать, что оно равно 1.

Упражнение 27*. Докажите эту гипотезу. ((Hint: prove, that (-1)(-1) + (-1)=0)