
- •8)Алгоритм построения днф
- •Алгоритм построения кнф
- •Унарные функции
- •2) Бинарные функции
- •1.4. Полный одноразрядный двоичный сумматор
- •4)Операции над предикатами
- •Логические операции
- •Кванторные операции
- •8) Сколемовская нормальная форма
- •Алгоритм приведения к сколемовской нормальной форме
- •10) Метод резолюции
1)Высказывания и операции над ними. Под высказыванием понимают грамматически правильное повествовательное предложение, про которое можно сказать, что оно либо истинно, либо ложно
1) отрицание: А
2) дизъюнкция: А В
3) конъюнкция: А В
4) импликация: А → В
5) эквивалентность: В ~ А
2)Формулы А.В и их виды
1.
|
|
2.
|
Законы |
3.
|
де Моргана |
4.
|
|
5.
|
|
Эти фомулы могут быть доказаны сравнением соответствующих таблиц истинности.
Из двух высказываний А и В можно составить четыре импликации, которые носят название
A
![]() B
прямая
теорема
B
A
обратная
теорема
B
прямая
теорема
B
A
обратная
теорема
![]()
![]() противоположная
теорема
теорема
противоположная к обратной
противоположная
теорема
теорема
противоположная к обратной
Из основных формул алгебры высказываний следует, что
(
A
B
)
![]() (
)
(
B
A
)
(
)
(
)
(
B
A
)
(
)
Следует отметить, что из истинности прямой теоремы еще не следует истинность обратной к ней теоремы, как это видно из примера 1.1.1.
Доказать истинность теоремы ( A B ) можно, доказав истинность теоремы ( ) , так как эти теоремы эквивалентны. На этом основано доказательство от противного теоремы ( A B ) , а именно, имея истинность , предполагая истинность , и доказав, что из следует , мы получаем противоречие ( A и одновременно истинны ), что не может быть, значит - ложно, тогда В - истинно и, значит, импликация A B - истинна.
3) Правила получения тавтологий. Формула является тождественно истинной, если она истинна при любых значениях входящих в неё переменных. Вот несколько широко известных примеров тождественно истинных формул логики высказываний:
Законы де Моргана:
1)
![]() ;
;
2)
![]() ;
;
Закон контрапозиции:
![]() ;
;
Законы поглощения:
1)
![]() ;
;
2)
![]() ;
;
Законы дистрибутивности:
1)
![]() ;
;
2)
![]() .
.
4)Логическое следствие.
Доказательство
теорем сводится к доказательству того,
что некоторая формула
![]() (гипотеза
теоремы) является логическим следствием
множества формул
(гипотеза
теоремы) является логическим следствием
множества формул
![]() (допущений).
Т.е. сама теорема может быть сформулирована
следующим образом: "если
истинны,
то истинна и
".
Такой метод доказательства теорем
называется методом
резолюций.
(допущений).
Т.е. сама теорема может быть сформулирована
следующим образом: "если
истинны,
то истинна и
".
Такой метод доказательства теорем
называется методом
резолюций.
Для
доказательства того, что формула G
является логическим следствием множества
формул
,
метод резолюций применяется следующим
образом. Сначала составляется множество
формул
![]() .
Затем каждая из этих формул приводится
к КНФ
(конъюнкция дизъюнктов) и в полученных
формулах зачеркиваются знаки конъюнкции.
Получается множество дизъюнктов S. И,
наконец, ищется вывод пустого дизъюнкта
из S. Если пустой дизъюнкт выводим из S,
то формула G является логическим
следствием формул
.
Если из S нельзя вывести #, то G не является
логическим следствием формул
.
.
Затем каждая из этих формул приводится
к КНФ
(конъюнкция дизъюнктов) и в полученных
формулах зачеркиваются знаки конъюнкции.
Получается множество дизъюнктов S. И,
наконец, ищется вывод пустого дизъюнкта
из S. Если пустой дизъюнкт выводим из S,
то формула G является логическим
следствием формул
.
Если из S нельзя вывести #, то G не является
логическим следствием формул
.
5) Равносильность.Определение. Пусть А и В – две формулы, зависящие от одного и того же списка переменных. Будем называть их равносильными, если для любого набора значений переменных они принимают одинаковые значения.
Рассмотрим основные равносильности логики высказываний.
Пусть А, В, С – произвольные формулы. Тогда справедливы следующие свойства логических операций
1. Идемпотентность |
||
А Щ А = А |
А Ъ А = А |
|
2. Коммутативность |
||
А Щ В = В Щ А |
А Ъ В = В Ъ А |
|
3. Ассоциативность |
||
А Щ (В Щ С) = (А Щ В) Щ С |
А Ъ (В Ъ С) = (А Ъ В) Ъ С |
|
4. Правила поглощения |
||
А Щ (А Ъ В) = А |
А Ъ (А Щ В) = А |
|
5. Дистрибутивность |
||
А Щ (В Ъ С) = (А Щ В) Ъ (А Щ С) |
А Ъ (В Щ С) = (А Ъ В) Щ (А Ъ С) |
|
6. Правила де Моргана |
||
|
|
|
7. Свойства констант |
||
А Щ 1 = А А Щ 0 = 0 |
А Ъ 0 = А А Ъ 1 = 1 |
|
8. Закон исключения третьего и закон противоречия |
||
|
|
|
9. Снятие двойного отрицания |
||
|
|
|
10. Формулы расщепления (склеивания) |
||
|
|
|
11. Связь дизъюнкции, конъюнкции, отрицания и импликации |
||
|
||
12. Выражение эквивалентности |
||
|
||
6)
Бинарное
отношение
![]() на
множестве
на
множестве
![]() называется
отношением
эквивалентности,
если оно обладает следующими свойствами:
называется
отношением
эквивалентности,
если оно обладает следующими свойствами:
Рефлексивность:
 .
.
Симметричность:
 если
если
 ,
то
,
то
 .
.
Транзитивность:
 если
и
если
и
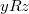 ,
то
,
то
 .
.
Отношение эквивалентности обозначают
символом
![]() .
Запись вида
.
Запись вида
![]() читают
как "
читают
как "![]() эквивалентно
эквивалентно
![]() "
"
Отношение равенства(
 )
является тривиальным примером отношения
эквивалентности на любом множестве.
)
является тривиальным примером отношения
эквивалентности на любом множестве.
Отношение равенства по модулю
 :
:
 на
множестве целых чисел.
на
множестве целых чисел.
Отношение параллельности прямых на плоскости.
Отношение подобия фигур на плоскости.
Отношение равносильности на множестве уравнений.
Отношение связности вершин в графе.
Отношение быть одного роста на множестве людей.
Следующие отношения не являются отношениями эквивалентности:
Отношения порядка, так как они не являются симметричными.
Отношение быть знакомым на множестве людей, так как оно не транзитивное.
Определение: |
||
Система
непустых подмножеств
Множества
|
||
|
|
|
7) Основные равносильности Закон двойного отрицания
![]()
![]()
Идемпотентность
![]()
![]()
![]()
![]()
Коммутативность
![]()
![]()
![]()
![]()
Ассоциативность
![]()
![]()
![]()
![]()
![]()
Дистрибутивность
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Законы де Моргана
![]()
![]()
![]()
![]()
Формулы с константами
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
8)Алгоритм построения днф
1) Избавиться от всех логических операций, содержащихся в формуле, заменив их основными: конъюнкцией, дизъюнкцией, отрицанием. Это можно сделать, используя равносильные формулы:
![]()
![]()
2) Заменить знак отрицания, относящийся ко всему выражению, знаками отрицания, относящимися к отдельным переменным высказываниям на основании формул:
![]()
![]()
3) Избавиться от знаков двойного отрицания.
4) Применить, если нужно, к операциям конъюнкции и дизъюнкции свойства дистрибутивности и формулы поглощения.
Алгоритм построения кнф
1) Избавиться от всех логических операций, содержащихся в формуле, заменив их основными: конъюнкцией, дизъюнкцией, отрицанием. Это можно сделать, используя равносильные формулы:
2) Заменить знак отрицания, относящийся ко всему выражению, знаками отрицания, относящимися к отдельным переменным высказываниям на основании формул:
3) Избавиться от знаков двойного отрицания.
4) Применить, если нужно, к операциям конъюнкции и дизъюнкции свойства дистрибутивности и формулы поглощения.
9)Если в какой-то простой
конъюнкции недостает переменной,
например, Z, вставляем в нее выражение :,после
чего раскрываем скобки (при этом
повторяющиеся дизъюнктные слагаемые
не пишем). Например:
![]()
![]()
-Y-ZV-X-Y-Z
![]()
Таким образом, из ДНФ получили СДНФ.
Если
в простой дизъюнкции не хватает какой-то
переменной (например, z, то добавляем в
нее выражение :![]() (это не меняет самой дизъюнкции), после
чего раскрываем скобки с использованием
распределительного
закона):
(это не меняет самой дизъюнкции), после
чего раскрываем скобки с использованием
распределительного
закона):
![]()
-YV-Z)
Таким образом, из КНФ получена СКНФ.
Булевы функции
1)
Унарные функции
При n = 1 число булевых функций равно 221 = 22 = 4. Определение этих функций содержится в следующей таблице.
Таблица значений булевых функций от одной переменной:
x |
0 |
x̅ |
x |
1 |
|
|
0 |
0 |
1 |
0 |
1 |
|
|
1 |
0 |
0 |
1 |
1 |
|
|
|
|
|||||
0 |
тождественный ноль, тождественная ложь, тождественное "НЕТ" |
|||||
x̅, ¬x, x' |
отрицание, логическое "НЕТ", "НЕ", "НИ", "NOT"(англ.), "NO"(англ.) |
|||||
x |
тождественная функция, логическое "ДА", "YES"(англ.) |
|||||
1 |
тождественная единица, тождественная истина, тождественное "ДА", тавтология |
|||||
2) Бинарные функции
При n = 2 число булевых функций равно 22² = 24 = 16.
x |
y |
0 |
x↓y |
x←y |
x |
x→y |
y |
x⊕y |
x|y |
x & y |
x ≡ y |
y |
x→y |
x |
x←y |
x ∨ y |
1 |
|
0 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
|
0 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
|
1 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
|
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
|
|
|||||||||||||||||
0 |
тождественный ноль, тождественная ложь, тождественное "НЕТ" |
|||||||||||||||||
x ↓ y, x ИЛИ-НЕ y, ИЛИ-НЕ(x,y), x NOR y, NOR(x,y) |
НЕ- 2ИЛИ, 2ИЛИ-НЕ, антидизъюнкция, функция Да́ггера, функция Ве́бба, стрелка Пи́рса |
|||||||||||||||||
x < y, x ← y, x LT y, LT(x,y) |
меньше, инверсия обратной импликации |
|||||||||||||||||
x, НЕ1(x,y), NOT1(x,y), x', ¬x |
отрицание (негация, инверсия) первого операнда |
|||||||||||||||||
x > y, x → y, x GT y, GT(x,y) |
больше, инверсия прямой импликации |
|||||||||||||||||
y, НЕ2(x,y), NOT2(x,y), y', ¬y |
отрицание (негация, инверсия) второго операнда |
|||||||||||||||||
x ⊕ y, x +2 y, x ≠ y, x >< y, x <> y, x XOR y, XOR(x,y) |
сложение по модулю 2, не равно, измена, исключающее «или» |
|||||||||||||||||
x | y, x NAND y, NAND(x,y), x И-НЕ y, И-НЕ(x,y) |
НЕ-2И, 2И-НЕ, антиконъюнкция, штрих Ше́ффера |
|||||||||||||||||
x & y, x · y, xy, x ∧ y, x AND y, AND(x,y), x И y, И(x,y), min(x,y) |
2И, конъюнкция |
|||||||||||||||||
x ≡ y, x = y, x EQV y, EQV(x,y), x ~ y, x ↔ y |
равенство, эквивалентность |
|||||||||||||||||
y, ДА2(x,y), YES2(x,y) |
второй операнд |
|||||||||||||||||
x → y, x ≤ y, x ⊃ y, x LE y, LE(x,y) |
меньше или равно, прямая (материальная) импликация (от первого аргумента ко второму) |
|||||||||||||||||
x, ДА1(x,y), YES1(x,y) |
первый операнд |
|||||||||||||||||
x ← y, x ≥ y, x ⊂ y, x GE y, GE(x,y) |
больше или равно, обратная импликация (от второго аргумента к первому) |
|||||||||||||||||
x ∨ y, x + y, x ИЛИ y, ИЛИ(x,y), x OR y, OR(x,y), max(x,y) |
2ИЛИ, дизъюнкция тождественная единица, тождественная истина, тождественное "ДА", тавтология |
|||||||||||||||||
5) Система булевых функций называется полной, если можно построить их суперпозицию, тождественную любой другой заранее заданной функции. Говорят ещё, что замыкание данной системы совпадает с множеством P2. Американский математик Эмиль Пост ввёл в рассмотрение следующие замкнутые классы булевых функций:
Им было доказано, что любой замкнутый класс булевых функций, не совпадающий с P2, целиком содержится в одном из этих пяти так называемых предполных классов, но при этом ни один из пяти не содержится целиком в объединении четырёх других. Таким образом критерий Поста для полноты системы сводится к выяснению, не содержится ли вся эта система целиком в одном из предполных классов. Если для каждого класса в системе найдётся функция, не входящая в него, то такая система будет полной, и с помощью входящих в неё функций можно будет получить любую другую булеву функцию. Заметим, что существуют функции, не входящие ни в один из классов Поста. Любая такая функция сама по себе образует полную систему. В качестве примеров можно назвать штрих Шеффера или стрелку Пирса.
|
|
|||||||||||||||||
Определение.
Алгеброй Жегалкина называется алгебра
над множеством логических функций и
переменных, сигнатура которой содержит
две бинарные операции & и
![]() ,
и две нульарные операции – константы
0 и 1.
,
и две нульарные операции – константы
0 и 1.
В алгебре Жегалкина выполняются следующие соотношения:
1. x y = y x;
2. x ( y z ) = x y x z;
3. x x = 0;
(1.4)
4.
x
![]() =
1;
=
1;
5. x 0 = x.
Эти соотношения легко проверить табличным способом. Кроме перечисленных соотношений в алгебре Жегалкина выполняются соотношения булевой алгебры относительно конъюнкции и констант
.
Найдем выражения для основных элементарных функций алгебры логики в алгебре Жегалкина.
1. = x 1.
Это соотношение проверяется непосредственной подстановкой 0 и 1 в обе части равенства.
x
![]() y
= x y
x
y.
y
= x y
x
y.
Доказательство:
x
y
=
![]() =
=
![]() 1
= ( x
1
)( y
1
)
1
=
1
= ( x
1
)( y
1
)
1
=
= x y x y 1 1 = x y x y.
3. x ’ y = x y x 1.
Доказательство: Используем выражение для импликсации в (1.3). Тогда:
x ’ y = y = y y = ( x 1 ) y ( x 1 ) y =
= x y y x 1 y = x y x 1.
4. x / y = x y 1.
Доказательство: Используем выражение для x / y в (1.3). Тогда:
x
/ y =
![]() =
xy
1.
=
xy
1.
5. x “ y = x y x y 1.
Доказательство: Используем выражение для x “ y в (1.3). Тогда:
x “ y = = ( x 1 )( y 1) = x y x y 1.
6.
x
~ y = 1
![]() x
y.
x
y.
Доказательство:
Легко
проверить, что x ~ y = x y![]()
![]()
![]() .
Тогда :
.
Тогда :
x ~ y = x y ( x 1 )( y 1 ) = x y x y x y 1 = 1 x y.
Определение. Полиномом Жегалкина для n логических переменных называется полином, являющийся суммой константы и различных одночленов, в которые все пере-
менные входят не выше, чем в первой степени:
a
x![]() x
x![]() … x
… x![]() , ( 1 d k d n )
, ( 1 d k d n )
причем
в каждом наборе ( i![]() ,
, i
,
, i![]() ) все i
) все i![]() различны, а суммирование по mod 2 ведется
по некоторому множеству таких не
совпадающих наборов.
различны, а суммирование по mod 2 ведется
по некоторому множеству таких не
совпадающих наборов.
Например,
1
x
x
x![]() , x
x
x
, x
x
x![]() x
x
x
- некоторые полиномы Жегалкина для двух
и трех переменных соответственно.
x
x
x
- некоторые полиномы Жегалкина для двух
и трех переменных соответственно.
От формулы алгебры логики всегда можно перейти к формуле алгебры Жегалкина. Для этого нужно заменить основные элементарные функции алгебры логики на соответствующие эквивалентные выражения алгебры Жегалкина (1) - (5), представленные выше.
В полученной формуле нужно раскрыть скобки и произвести упрощения, используя соотношения (1.4), а также следующие соотношения: x & x = x и x·1 = x. Полученное выражение и будет полиномом Жегалкина для данной формулы.
Пример.
Найти полином Жегалкина для функции:
f( x, y ) = ( x
y
)(
![]() x
z ).
x
z ).

Полученное выражение и есть полином Жегалкина.
При нахождении полинома Жегалкина для некоторой формулы алгебры логики можно использовать следующее соотношение, вытекающее из представления дизъюнкции в алгебре Жегалкина:
f1 f2 = f1 f2, (1.5)
справедливое при f1f2 = 0. Используем соотношение (1.5) для нахождения полинома Жегалкина в следующих примерах.
Пример.
Найти полином Жегалкина для функции:
f( x, y ) = x y
![]() .
.
Сделаем следующие преобразования:
f(
x,y ) = x y
![]() =
x y
=
x y
(
x
1
)( y
1
) =
=
x y
=
x y
(
x
1
)( y
1
) =
= x y x y x y 1 = 1 x y - полиномом Жегалкина.
Пример. Найти полином Жегалкина для функции: f( x, y ) = x z.
Сделаем следующие преобразования:
f(
x,y ) = x
z
= x
![]() z
= x ( y
1
)
(
x
1
) z =
z
= x ( y
1
)
(
x
1
) z =
= x y x x z z = x z x y x z. - полиномом Жегалкина.
Теорема. Для любой логической функции существует полином Жегалкина и притом единственный.
Доказательство: Существование полинома доказано вышеприведенным алгоритмом получения полинома из логической формулы. Для доказательства единственности надо показать, что между множеством всех логических функций от n переменных и множеством всех полиномов Жегалкина от n переменных существует взаимно однозначное соответствие.
Полином Жегалкина можно найти методом неопределенных коэффициентов. Рассмотрим этот метод на следующим примере.
Пример. Найти полином Жегалкина для функции заданной векторно:
f( x,y ) = ( 0, 1, 1, 0 ).
Составим таблицу 1.14 задания данной функции.
Таблица 1.14
x |
y |
f |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
Полином Жегалкина для функции двух переменных ищем в следующем виде:
f( x, y ) = a0 a1·x a2·y a3·xy (1.6)
Для определения коэффициентов полинома нужно подставить значения неизвестных и соответствующее значение функции в (1.6), согласно таблице 1.14.
Подставляя набор переменных(0,0) в (1.6) получим:
![]() .
.
![]() a
a![]() = 0.
= 0.
Аналогично для набора (0,1) получим:
![]() .
a
= 1.
.
a
= 1.
Для
набора (1,0) получим:
![]() a
= 1.
a
= 1.
Для
набора (1,1) получим:
![]() a
= 0.
a
= 0.
Подставляя в (1.6) найденные значения коэффициентов получим искомый полином для данной функции:
f( x, y ) = x y.
Замечание.
Можно показать, что переменная
x![]() будет фиктивной
для некоторой функции тогда и только
тогда, когда полином Жегалкина для нее
не содержит переменной x
будет фиктивной
для некоторой функции тогда и только
тогда, когда полином Жегалкина для нее
не содержит переменной x
?) Теорема Поста открывает путь к
представлению булевых функций
синтаксическим способом, который в ряде
случаев оказывается намного удобнее
чем таблицы истинности. Отправной точкой
здесь служит нахождение некоторой
полной системы функций
![]() .
Тогда каждая булева функция сможет быть
представлена некоторым термом
в сигнатуре
Σ, который в данном случае называют
также формулой.
Относительно выбраной системы функций
полезно знать ответы на следующие
вопросы:
.
Тогда каждая булева функция сможет быть
представлена некоторым термом
в сигнатуре
Σ, который в данном случае называют
также формулой.
Относительно выбраной системы функций
полезно знать ответы на следующие
вопросы:
Как построить по данной функции представляющую её формулу?
Как проверить, что две разные формулы эквивалентны, то есть задают одну и ту же функцию?
В частности: существует ли способ приведения произвольной формулы к эквивалентной её канонической форме, такой что, две формулы эквивалентны тогда и только тогда, когда их канонические формы совпадают?
Как по данной функции построить представляющую её формулу с теми или иными заданными свойствами (например, наименьшего размера), и возможно ли это?
Положительные ответы на эти и другие вопросы существенно увеличивают прикладное значение выбранной системы функций.
13) Лемма о нелинейной функции.
Суперпозицией нелинейной функции, отрицания и константы 1 можно получить конъюнкцию.
Доказательство: Пусть f(x1,…, xn ) – нелинейная функция, тогда полином Жигалкина для нее содержит слагаемое, в котором присутствует произведение каких-то переменных xi*xj. Пусть для простоты это будет произведение х1х2. Произведя группировку слагаемых в полиноме Жегалкина для f относительно x1х2, х1, х2, функцию f представим в виде f(x1,…, xn)=x1*x2*h0(x3,..,xn)+ {собрали все слагаемые с x1*x2 и вынесли x1*x2 за скобки. В скобках осталась сумма h0(x3,…,xn), в которой переменных x1, x2 нет} + x1*h1(x3,…, xn) + x2*h2(x3,…, xn) + h3(x3,…, xn)
Функция h0(x3,…, xn)≠0, в противном случае многочлен Жигалкина слагаемых с произведением x1x2 не имеет, тогда существует набор (a3,…, an) из 0 и1, для которого h0(a3,…, an)=1. Пусть на этом наборе h1(a3,…, an)=a h2(a3,…, an)=b h3(a3,…, an)=c. Тогда функция g(x1,x2)=f(x1,x2,a3,…, an)=x1*x2+a*x1+b*x2+c. Построим функцию h(x1,x2) = g(x1+bx2+a) = (x1+b)(x2+a)+a(x1+b)+b(x2+a)+c = x1*x2+a*x1+b*x2+a*b+a*x1+a*b+b*x2+a*b+c = x1*x2+a*b+c=x1*x2+d, d=a*b+c Если d=0, то h(x1,x2)=x1*x2, конъюнкция получена. Если d=1, то h(x1,x2)=x1*x2+1 ⇒ x1*x2=⌐h(x1,x2), что и требовалось доказать.
16) Релейно-контактные схемы (их часто называют переключательными схемами) широко используются в технике автоматического управления.
Под переключательной схемой понимают схематическое изображение некоторого устройства, состоящее из следующих элементов:
1) переключателей, которыми могут быть механические устройства, электромагнитные реле, полупроводники и т.д.;
2) соединяющие их проводники;
3) входы в схему и выходы из нее (клеммы, на которые подается электрическое напряжение). Они называются полюсами.
Простейшая
схема содержит один переключатель Р
и имеет один вход А
и один выход В.![]() Переключателю Р
поставим в соответствии высказывание
р,
гласящее: - “Переключатель Р
замкнут ”. Если р
истинно, то импульс, поступающий на
полюс А,
может быть снят на полюсе В
без потери напряжения, то есть схема
пропускает ток. Если р
ложно, то переключатель разомкнут и
схема тока не проводит. Таким образом,
если принять во внимание не смысл
высказывания, а только его значение, то
можно считать, что любому высказыванию
может быть поставлена в соответсвие
переключательная схема с двумя полюсами
(двухполюсная схема).
Переключателю Р
поставим в соответствии высказывание
р,
гласящее: - “Переключатель Р
замкнут ”. Если р
истинно, то импульс, поступающий на
полюс А,
может быть снят на полюсе В
без потери напряжения, то есть схема
пропускает ток. Если р
ложно, то переключатель разомкнут и
схема тока не проводит. Таким образом,
если принять во внимание не смысл
высказывания, а только его значение, то
можно считать, что любому высказыванию
может быть поставлена в соответсвие
переключательная схема с двумя полюсами
(двухполюсная схема).
Формулам, включающим основные логические операции, также могут быть поставлены в соответствие переключательные схемы.
![]()
Так,
конъюнкции двух высказываний
![]() ставится в соответствие схема:
ставится в соответствие схема:
![]()
а
дизъюнкции
![]() - схема:
- схема:

Так как любая формула может быть записана в ДНФ или КНФ, то ясно, что каждой формуле алгебры логики можно поставить в соответствие некоторую РКС, а каждой РКС можно поставить в соответствие некоторую формулу алгебры логики.
Пример
1. По данной формуле составить РКС
![]() .
.
Решение. Упростим данную формулу с помощью равносильных преобразований:


Тогда РКС для данной формулы имеет вид:
Пример 2. Упростить РКС:

Решение. Составим по данной РКС формулу (функцию проводимости) и упростим ее:
![]()
(к последним двум слагаемым применили закон поглощения).
Тогда упрощенная схема выглядит так:
![]()
18) Полусумматор — логическая схема, имеющая два входа и два выхода (двухразрядный сумматор, бинарный сумматор). Полусумматор используется для построения двоичных сумматоров. Полусумматор позволяет вычислять сумму A+B, где A и B — это разряды двоичного числа, при этом результатом будут два бита S,C, где S — это бит суммы по модулю, а C — бит переноса. Однако, как можно заметить, для построения схемы двоичного сумматора (трёхразрядный сумматор, тринарный сумматор) необходимо иметь элемент, который суммирует три бита A, B и C, где C — бит переноса из предыдущего разряда, таким элементом является полный двоичный сумматор, который как правило состоит из двух полусумматоров и логического элемента 2ИЛИ. Представляет собой объединение двух бинарных (двухоперандных) двоичных логических функций: сумма по модулю два - S и разряд переноса при двоичном сложении - C.
