
- •Этапы решения
- •Транспортная задача. Постановка задачи.
- •Опорный план.
- •Методы поиска опорного плана. Метод северо-западного угла.
- •Методы поиска опорного плана. Метод потенциалов.
- •Методы поиска опорного плана. Метод минимального тарифа (элемента).
- •Методы поиска опорного плана. Метод Фогеля.
- •Критерий оптимальности транспортной задачи (Условие оптимальности опорного плана?).
- •Алгоритм перехода к новому опорному плану (алгоритм перехода к нехудшему опорному плану?).
- •Транспортная задача с ограничениями на пропускную способность (решение транспортной задачи с ограничениями?).
- •Метод фогеля
- •Метод ближайшего соседа
- •Вопрос 18.
Постановка задачи принятия решения
ЦФ
:
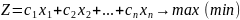
c- доход от продажи изделия, n – количество видов продукта, x – количество объема производства продуктов.
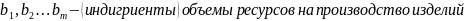
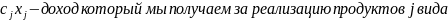
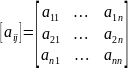 – технологическая
матрица
– технологическая
матрица
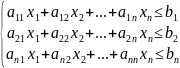
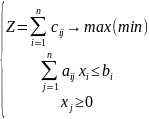
Основные понятия:
Альтернатива – множество возможных решений.
Принцип -
Критерий оптимальности – существенная характеристика альтернативы, которая позволяет сравнивать альтернативы между собой.
ЛПР – лицо принимающие решение (еще и отвечающие за его последствия), должен обладать ресурсами для реализации решения.
Типы и классификация задач : однокритериальные и многокритериальные.
Этапы решения задачи: наверное построение задачи, нахождение опорного плана, проверка на оптимальность, решение.
Среда ПР: детерминированная (определенная), вероятностно (статически) определенная, неопределенная (принятие решения в условиях риска), нечеткая (неполные условия).
Количественные и качественные МПР: методы анализа иерархии, методы экспертных оценок, методы искусственного интеллекта, методы теории игр.
В процессе проектирования ставится обычно задача определения наилучших, в некотором смысле, структуры или значений параметров объектов. Такая задача называется оптимизационной. Если оптимизация связана с расчетом оптимальных значений параметров при заданной структуре объекта, то она называется параметрической оптимизацией. Задача выбора оптимальной структуры является структурной оптимизацией.
Стандартная математическая задача оптимизации формулируется таким образом. Среди элементов χ, образующих множества Χ, найти такой элемент χ* , который доставляет минимальное значение f(χ*) заданной функции f(χ). Для того, чтобы корректно поставить задачу оптимизации необходимо задать:
Допустимое множество — множество
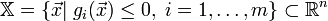 ;
;Целевую функцию — отображение
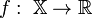 ;
;Критерий поиска (max или min).
Тогда решить
задачу ![]() означает
одно из:
означает
одно из:
Показать, что
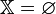 .
.Показать, что целевая функция
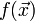 не
ограничена снизу.
не
ограничена снизу.
Найти
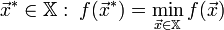 .
.
Если
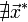 ,
то найти
,
то найти 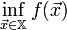 .
.
Если минимизируемая
функция не является выпуклой,
то часто ограничиваются поиском локальных
минимумов и максимумов: точек x0 таких,
что всюду в некоторой их окрестности ![]() для
минимума и
для
минимума и ![]() для
максимума.
для
максимума.
Если допустимое
множество ![]() ,
то такая задача называется задачей
безусловной оптимизации,
в противном случае — задачей
условной оптимизации.
,
то такая задача называется задачей
безусловной оптимизации,
в противном случае — задачей
условной оптимизации.
Классификация методов оптимизации
Общая запись задач оптимизации задаёт большое разнообразие их классов. От класса задачи зависит подбор метода (эффективность её решения). Классификацию задач определяют: целевая функция и допустимая область (задаётся системой неравенств и равенств или более сложным алгоритмом)[1].
Методы оптимизации классифицируют в соответствии с задачами оптимизации:
Локальные методы: сходятся к какому-нибудь локальному экстремуму целевой функции. В случае унимодальной целевой функции, этот экстремум единственен, и будет глобальным максимумом/минимумом.
Глобальные методы: имеют дело с многоэкстремальными целевыми функциями. При глобальном поиске основной задачей является выявление тенденций глобального поведения целевой функции.
Существующие в настоящее время методы поиска можно разбить на три большие группы:
детерминированные;
случайные (стохастические);
комбинированные.
По критерию размерности допустимого множества, методы оптимизации делят на методы одномерной оптимизации и методы многомерной оптимизации.
По виду целевой функции и допустимого множества, задачи оптимизации и методы их решения можно разделить на следующие классы:
Задачи оптимизации, в которых целевая функция и ограничения
 являются
линейными функциями, разрешаются так
называемыми методами линейного
программирования.
являются
линейными функциями, разрешаются так
называемыми методами линейного
программирования.В противном случае имеют дело с задачей нелинейного программирования и применяют соответствующие методы. В свою очередь из них выделяют две частные задачи:
если и — выпуклые функции, то такую задачу называют задачей выпуклого программирования;
если
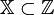 ,
то имеют дело с задачей целочисленного
(дискретного) программирования.
,
то имеют дело с задачей целочисленного
(дискретного) программирования.
По требованиям к гладкости и наличию у целевой функции частных производных, их также можно разделить на:
прямые методы, требующие только вычислений целевой функции в точках приближений;
методы первого порядка: требуют вычисления первых частных производных функции;
методы второго порядка: требуют вычисления вторых частных производных, то есть гессиана целевой функции.
Помимо того, оптимизационные методы делятся на следующие группы:
аналитические методы (например, метод множителей Лагранжа и условия Каруша-Куна-Таккера);
численные методы;
графические методы.
В зависимости от природы множества X задачи математического программирования классифицируются как:
задачи дискретного программирования (или комбинаторной оптимизации) — если X конечно или счётно;
задачи целочисленного программирования — если X является подмножеством множества целых чисел;
задачей нелинейного программирования, если ограничения или целевая функция содержат нелинейные функции и X является подмножеством конечномерного векторного пространства.
Если же все ограничения и целевая функция содержат лишь линейные функции, то это — задача линейного программирования.
Кроме того, разделами математического программирования являются параметрическое программирование, динамическое программирование и стохастическое программирование. Математическое программирование используется при решении оптимизационных задач исследования операций.
Способ нахождения экстремума полностью определяется классом задачи. Но перед тем, как получить математическую модель, нужно выполнить 4 этапа моделирования:
Определение границ системы оптимизации
Отбрасываем те связи объекта оптимизации с внешним миром, которые не могут сильно повлиять на результат оптимизации, а, точнее, те, без которых решение упрощается
Выбор управляемых переменных
«Замораживаем» значения некоторых переменных (неуправляемые переменные). Другие оставляем принимать любые значения из области допустимых решений (управляемые переменные)
Определение ограничений на управляемые переменные
… (равенства и\или неравенства)
Выбор числового критерия оптимизации
Создаём целевую функцию
Многие задачи оптимизации формулируются следующим образом. Решение, которое должен принять субъект, описывается набором чисел х1 ,х2 ,…,хn (или точкой Х=(х1 ,х2 ,…,хn) n-мерного пространства). Достоинства того или иного решения определяются значениями функция f(X) = f(х1, х2 ,…,хn) -- целевой функции. Наилучшее решение -- это такая точка Х, в которой функция f(Х) принимает наибольшее значение. Задача нахождения такой точки описывается следующим образом:
f(X) max.
Если функция f(X) характеризует отрицательные стороны решения (ущерб, убытки и т. п.), то ищется точка Х, в которой значение f(X) минимально:
f(X) min.
Будем говорить только о задачах максимизации. Поиск минимума не требует специального рассмотрения, поскольку заменой целевой функции f(X) на -f(Х) всегда можно “превратить недостатки в достоинства” и свести минимизацию к максимизации.
Из каких вариантов должен быть выбран наилучший? Иными словами, среди каких точек пространства нужно искать оптимум. Ответ на этот вопрос связан с таким элементом оптимизационной задачи, как множество допустимых решений. В некоторых задачах допустимыми являются любые комбинации чисел х1, х2,…,хn то есть множество допустимых решений - это все рассматриваемое пространство.
В других задачах следует принимать во внимание различные ограничения, означающие, что не все точки пространства доступны при выборе. В содержательных постановках задач это может быть связано, например, с ограниченностью располагаемого количества ресурсов.
Ограничения могут быть представлены в форме равенств вида
g(X) = О
или неравенства
g(X) О.
Если условия имеют несколько другую форму, скажем, g1(Х) = g2(X) или g(X) A, то их можно привести к стандартному виду, перенеся в функции и константы в одну из частей равенства или неравенства.
Качественные модели принятия решений. Постановка задачи. Понятия среды принятия решений. Факторы, влияющие
(Далее типа для внутренней среды принятия решений).
При принятии управленческих решений всегда важно учитывать риск. Понятие «риск» используется здесь не в смысле опасности. Риск скорее относится к уровню определенности, с которой можно прогнозировать результат.
В ходе оценки альтернатив и принятия решений руководитель должен прогнозировать возможные результаты в разных обстоятельства или состояниях природы. По сути дела, решения принимаются в разных обстоятельствах по отношению к риску. Эти обстоятельства традиционно классифицируются как условия определенности, риска или неопределенности.
Определенность. Решение принимается в условиях определенности, когда руководитель в точности знает результат каждого из альтернативных вариантов выбора. Примером определенного решения может быть вложение избыточной наличности в 10%-е депозитные сертификаты. Руководитель знает, что, за исключением возникновения крайне маловероятных чрезвычайных обстоятельств, вследствие чего федеральное правительство не сможет выполнить свои обязательства, организация получит ровно 10% на вложенные средства. Подобным образом руководитель может, по меньшей мере на ближайшую перспективу, точно установить, какими будут затраты на производство определенного изделия, поскольку арендная плата, стоимость материалов и рабочей силы известны или могут быть рассчитаны с высокой точностью.
Сравнительно немногие организационные или персональные решения принимаются в условиях определенности. Однако они имеют место, и зачастую элементы более крупных решений можно рассматривать как определенные. Авторы и исследователи экономико-математических методов называют ситуации с наличием определенности детерминистскими.
Среды бывают:
Хорошо структурированные (Допускают применение математических моделей)
Плохо (мало) структурированные.
Принятие решений - особый вид человеческой деятельности, направленный на выбор лучшей из имеющихся альтернатив.
. Многокритериальные задачи принятия решений: математическая модель, типы шкал, шкалы качественные и количественные, номинальные и др. Методы сравнения альтернатив на различных шкалах.
Многокритериальная задача – задача, где у альтернатив 2+ критерия. Критерии могут быть положительные и отрицательные. Значения критериев мы измеряем на шкалах.
Шкала – некоторая упорядоченная совокупность значений, которые может принимать критерий.
Типы шкал:
Именованная (наименований) – значения шкалы и объект, с которым соотносятся значения, никак не связаны (например, номер телефона). Самая грубая шкала.
Номинальная (классификационная) - шкала произвольных взаимооднозначных преобразований, в результате которых сохраняются отношения равенства и неравенства между числами. (то есть оценка есть некоторое преобразование, причем если знач1>знач2, то оценка1>оценка2 ).
Ранговая – свойство описывается целыми числами, напрямую связанными с описываемым свойством. Если с увеличением качества значение оценки растёт – прямая, если уменьшается – обратная.
Бальная. Ранг более крупная шкала.
Натуральная - значения оцениваются функцией. f(x), x принадлежит X, x1>x2, f(x1)>f(x2)
Интервалов – значения оцениваются функцией
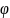 (х),
причём отношение интервалов между
значениями сохраняется. То есть
(х),
причём отношение интервалов между
значениями сохраняется. То есть
 =
= =const
=constШкала порядка.
Шкала отношений (подобия).
Качественная шкала – на данной шкале числовым промежуткам даются качественные оценки (плохо, средне, хорошо и т.п.). Например, значения 0 -3 оцениваются как плохо, 4 – 7 – хорошо, 8-10 – отлично.
Использование самых грубых шкал уже отсеивают до 80 процентов альтернатив ка не эффективных. Среди остальных 20 процентов можно определить половину альтернатив при использовании качественных шкал.
Из инета понятнее:
МНОГОКРИТЕРИАЛЬНАЯ ЗАДАЧА - математическая модель принятия оптимального решения одновременно по нескольким критериям. Эти критерии могут отражать оценки различных качеств объекта (или процесса), по поводу к-рых принимается решение, или оценки одной и той же его характеристики, но с различных точек зрения. Теория М. з. относится к числу ма-тематич. методов исследования операций.
Номинальная шкала
В шкале наименований допустимыми являются все взаимно-однозначные преобразования. В этой шкале числа используются как метки, только для различения объектов. В шкале наименований измерены, например, номера телефонов, автомашин, паспортов, студенческих билетов. Пол людей тоже измерен в шкале наименований, результат измерения принимает два значения - мужской, женский. Очевидно, что не имеет смысла складывать номера телефонов или умножать серии паспортов.
Порядковая шкала
В порядковой шкале числа используются не только для различения объектов, но и для установления порядка между объектами. Простейшим примером являются оценки знаний учащихся. Заметим, что в средней школе применяются оценки 2, 3, 4, 5, а в высшей школе ровно тот же смысл выражается словесно - неудовлетворительно, удовлетворительно, хорошо, отлично. Этим подчеркивается "нечисловой" характер оценок знаний учащихся. В порядковой шкале допустимыми являются все строго монотонные преобразования.
Шкала интервалов
По шкале интервалов измеряют величину потенциальной энергии или координату точки на прямой. В этих случаях на шкале нельзя отметить ни естественное начало отсчета, ни естественную единицу измерения. Исследователь должен сам задать точку отсчета и сам выбрать единицу измерения. Допустимыми преобразованиями в шкале интервалов являются линейные возрастающие преобразования, т.е. линейные функции. Температурные шкалы Цельсия и Фаренгейта связаны именно такой зависимостью: °C = 5/9 (°F - 32), где °C - температура (в градусах) по шкале Цельсия, а °F - температура по шкале Фаренгейта.
Шкала отношений
В шкалах отношений есть естественное начало отсчета - нуль, но нет естественной единицы измерения. По шкале отношений измерены большинство физических единиц: масса тела, длина, заряд, а также цены в экономике. Допустимыми преобразованиями шкале отношений являются подобные (изменяющие только масштаб). Другими словами, линейные возрастающие преобразования без свободного члена. Примеры использования таких преобразований: пересчет цен из одной валюты в другую по фиксированному курсу, перевод массы из килограмм в фунты.
Шкала разностей
В шкале разностей есть естественная единица измерения, но нет естественного начала отсчета. Время измеряется по шкале разностей, если год (или сутки - от полудня до полудня) принимаем естественной единицей измерения, и по шкале интервалов в общем случае. На современном уровне знаний естественного начала отсчета времени указать нельзя. Допустимыми преобразованиями шкале разностей являются сдвиги.
Абсолютная шкала
Только для абсолютной шкалы результаты измерений - числа в обычном смысле слова. Примером является число людей в комнате. Для абсолютной шкалы допустимым является только тождественное преобразование.
Иерархия шкал измерений
Слева - самая слабая шкала, справа - самая сильная.
(наименований<порядковая<интервалов<отношений=разностей<абсолютная)
Все шкалы делят также на 2 большие группы: качественные и количественные. К качественным шкалам относят номинальную и порядковую, к количественным - все остальные. Это разделение показывает разницу в природе шкал: например, невозможно утверждать, что школьная оценка 2 настолько же хуже оценки 4, насколько 3 хуже оценки 5, поэтому порядковые шкалы относят к качественным. В то же время, для тел разной массы аналогичное утверждение корректно: тело массой 5 кг настолько же тяжелее тела массой 3 кг, насколько тело массой 4 кг тяжелей тела массой 2 кг. Таким образом, шкалы отношений - это количественные шкалы.
Очевидно, что КДП одной шкалы может полностью включать в себя КДП другой. Тогда говорят, что вторая шкала сильнее первой. На иллюстрации изображена иерархия шкал.
Шкалы измерений и анализ данных
При анализе данных следует помнить о том, к какой шкале измерений относятся исследуемые величины: Алгоритм, применимый к более слабой шкале, применим и к более сильной.
Доминирование по Парето.
Многокритериальная оценка альтернатив
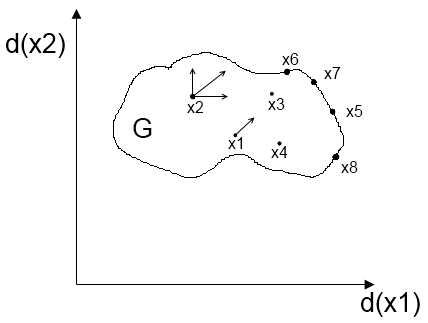
G – область допустимых решений окрестности ε.
1. Точки внутренние: все точки ∈ ε и ∈ G.
2. Точки граничные: точки ∈ ε и часть ∉ G. Их совокупность – граница G.
Оптимальное решение всегда надо искать среди граничных точек.
1. Точки, при движении которых значения x1 и x2 возрастают одновременно
2. Точки, при движении которых одна координата возрастает, другая постоянна(const)
3. Точки, при движении которых одна координата возрастает, а другая убывает.
Граница из точек 3-го типа – граница Парето.
Границы Парето:
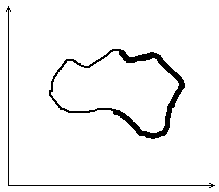

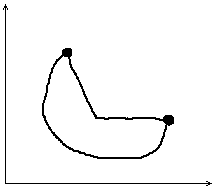
Многокритериальные оценки для сравнения n пер-к.
{a} = {a1, a2, …, an} – множество альтернатив
{F} = {f1, f2, …, fn}- критерии (множество оценочных функций)
Все fi(i = 1,m) определены на шкалах
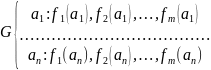
a1 – оценки первой альтернативы и т.д.
Каждую альтернативу мы можем описать оценкой, состоящей из m функций.
Все критерии независимы друг от друга
1. fi(aj) > fi(ak), i = 1,m; (j; k) = 1,n
Все значения j альтернатив по оценочным функциям больше k.
aj доминирует ak
aj – доминирующая альтернатива
ak – доминируемая альтернатива
a ≤ G (осталось подмножество с лучшей альтернативой)
2. fi(aj) ≥ fi(ak), fe(aj) ≥ fe(ak)
aj не лучше ak
aj >(PAR) ak не хуже ни по одной из оценок. >(PAR) означает, что над знаком > надо писать PAR
3. Несравнимые альтернативы (не выполняется условие доминирования)
Они образуют множество альтернатив 3-го типа не доминируемой ни одной из альтернатив всего множества – множество Парето.
Алгоритм формирования множества Парето:
1. {a} {F}
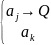
Q – множество Парето
aj >(PAR) ak
aj ⊂ Q
ak ⊂(перечёркнутая) G (исключается из множества)
ak >(PAR) aj
aj ∉ G
ak ∈ Q
aj и ak не сравниваются → ak ∈ Q
2. Следующая альтернатива al и пополняется множество Q
3. Сравнение альтернативы из множества Q. Выбрасываем доминируемые. В итоге получаем Q несравнимых альтернатив – эффективные альтернативы.
Принцип Парето:
Q ≤ G
Оптимальная альтернатива всегда находится среди альтернатив Паретова множества .
Недостаток – сглаживание критериев. Следовательно привлечение новой дополнительной информации от лица, принимающего решение.
Подходы к решению задач в рамках множества Парето - оптимальных исходов.
Методы сравнения альтернатив из множества Парето.
1. Метод главного критерия
2. Методы лексико – графической оптимизации
2.1. Метод нижних границ
2.2. Субоптимизация
2.3. Метод лексико - графического моделирования
2.3.1. Метод уступок
2.3.2. Метод точек безразличия
3. Метод обобщённого критерия
4. Метод анализа иерархии
5. Метод различия и сходства.
Метод главного критерия
1. Все критерии упорядочиваются по важности:
fi, I = 1,m – упорядочиваем
f1, f2, …, fm
2. Все альтернативы упорядочиваются по значению главного критерия (f1)
ai(f1max) – оптимальный
Если ai(f1max) = ak(f1max), то Q* = {ai, ak} … f2max
Недостаток: не учитывает важность остальных критериев.
Метод уступок
Δ f1max – уступка 1-го критерия
Q’ ⊂ Q – увеличивается важность критерия f2
Δ – компенсация для 2-го критерия
f2max(ai) → Q’’
Δ2 – уступка по 2-му критерию . Увеличивается важность f3. И так далее до fn
Получаем Δ1 , Δ2 , …, Δn-1 – ряд уступок
Лицо, принимающее решение, выбирает окончательные уступки (оптимальные). Таким обрахом выбирается та альтернатива, которая остаётся.
Метод точек безразличия
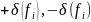
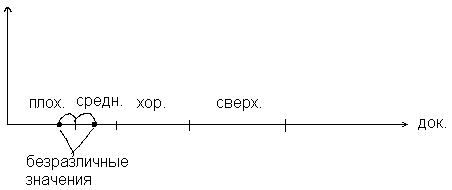
Метод нижних границ
Задаём границы
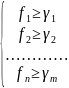
Грубый и жёсткий метод
Метод субоптимизации (строгое упорядочивание альтернатив)
Выбирается 1 главный критерий, а для остальных критериев назначаются границы. Упорядочиваем альтернативы по главному критерию.
Метод лексико - графического моделирования
Все критерии строго упорядочиваются по важности
f1, f2, …, fn
Все альтернативы упорядочиваются по критерию f1 и выбирается наилучшая. После упорядочиваем по критерию f2.

Недостатки: независимость критериев. Используя метод главного критерия, мы сводим задачу к однокритериальной, а значит получаем неадекватный результат.
Метод обобщённого критерия (многокритериальная оценка)
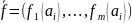 – векторное значение
– векторное значение
Переводим в скалярное значение.
Оптимизация осуществляется на скалярных значениях векторной функции альтернатив.
Правило Борда:
1) Все критерии ранжируются на одной однородной шкале
2) Каждой альтернативе по каждому из критериев fi ставится в соответствующее значение ранга
3) Наилучшей считается та альтернатива, где сумма ранговых оценок по всем критериям получается максимальной.
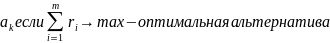
Многокритериальные задачи
Дано: A={A1,...,An}
Ai → (f1(Ai),f2(Ai),...,fn(Ai) ) где f1(Ai) — оценка а Ai — многокритериальная оценка.
Ai(i=1..n) принадлежит Gn, n — парето.
Процесс сравнения альтернатив заменяется сравнением оценок.
F(f1(Ai),f2(Ai),...,fn(Ai) ) i=1..n имеем матрицу оценок.
par
Ai>Aj ; если fk(Ai)≥fk(Aj) по всем доминирует по парето но для 1 будет fe(Ai)=fe(Aj)
Берется лучшее, но должно быть хотябы одно равное.
Парето множеством альтернатив называется множество, в котором ни одна из альтернатив не
доминируется с нижней другой. Происходит сужение до тех пор пока они не сравнимы.
Оптимальная альтернатива Ai* = (f1(Ai*),f2(Ai*),...,fn(Ai*) ) i=1..n. Оптимальная альтернатива
находится среди парето множества. Подходят к выбору по парето оптимальному множеству
альтернатив:
1. Когда задается нижняя граница значений критерий(например зарплата).
2. Субоптимизация. Apar=(A1,A2...An) — альтернативы попавшие в пограничное
множество. Среди критериев выбирается значительный. f1...fm → fi - наиболее
значительной для оси x: f1,fj-1,fj+1...fm — назначается нижняя граница. Оптимальная
альтернатива та у которой будет максимальное значение оценки по j критерию, все
остальные не хуже нижних границ.
3. Оптимизация по значимости критериев: fi>fj>fk>...>fm — цепочка значимости
критериев.
Достоинства многокритериальных задач:
Всегда сходятся, можно найти до одной альтернативы или сузить до малого количества
Недостатки:
Все они зависят от предпочтений ЛПР и субъективны.
Пример:
K1 — площадь
К2 — расстояние до метро
К3 — цена.
К4 — качество окружающей среды.
Задача — выбор квартиры.
Ai |
K1+ |
K2- |
K3- |
K4+ |
A1 |
25 |
2 |
140000 |
3 |
A2 |
50 |
20 |
200000 |
5 |
A3 |
60 |
5 |
260000 |
4 |
A4 |
25 |
10 |
111000 |
4 |
A5 |
30 |
17 |
120000 |
2 |
A6 |
42 |
40 |
90000 |
1 |
A7 |
25 |
3 |
130000 |
2 |
Q={A1...A7}
1. K1>30, K2<15, K3<150000, K4>2
2. A3,A2,A6,A5,A1,A4,A7 A5,A1,A4,A2.
3. K1>K3>K2>K4 → A3,A2,A6,A5,A1,A4,A7 A6,A4,A5,A7,A1,A2,A3
Обобщенный критерий оптимизации в многокритериальной задаче принятия решения.
Q — множество альтернатив PAR, то y(y1,y2,...ym) y=f(a)=(f1(a),f2(a),....fm(a)).
Q ≤ y= y1 * y2 *...* ym f(a)=φ(f1(a),f2(a),....fm(a)). Q — выпуклое множество.
φ(a)=∑άj fj(a)=∑xj yj — взвешенная сумма(от 1 до m) оценок.
άjj — оценка важности. άj>0 чем больше άj тем важнее критерий.
Утверждения:
1. Пусть Q≤y — множество векторных оценок. y*=(y1*,y2*,...ym*); φ(y)=∑άj yj → max. Если
векторная оценка приносит max целевой функции, где очевидно что вес άj ≥0, то оценка y* является парето оптимальной во множестве Q.
2. Q≤y — выпуклое множество. Y* принадлежит Q — парето оптимальная, то найдутся
такие числа ά1 …. άm≥0 , что функция φ(y*)=∑άj y*j будет иметь максимальное
значение.
Задача оптимизации некоторого производственного процесса.
П=(x1,x2,...xn) — ресурсы n типов на производство 1 единицы продукта.
П=(y1,y2,...ym) — продукты m типов.
П1=(x,y)=(-x1,-x2,...-xn , y1,y2,...yn)
П2=(x2,y2)=(-x12,-x22,...-xn2 , y12,y22,...yn2)
Если xi≤x2j и yi ≥y2j и xi =x2j и yi =y2j то П1>П2 по PAR.
Обобщенный критерий:
mn
φ(a,b)(x,y)=(a*x)+(b*y)=∑aj yj - ∑bi xi ; (aj bi ≥ 0)
Экономический смысл оценок:
aj — расходы на ресурсы.
bi — доходы от производства.
φ(a,b)(x,y) — доход от производственного процесса.
Поиск весовых коэффициентов процесса методом нормализации.
y= y1 * y2 *...* yn — множество оценок.
m
φ(a)=∑aj yj → max
aj = 1/Mj , где Mj=max|fi(a)|
m
φ(a)=∑ fi(a)/Mj ; M1=900 M2=30 M3=60.
Ai |
K1 |
K2 |
K3 |
A1 |
900 |
20 |
60 |
A2 |
500 |
30 |
40 |
φ(A)=900/900+20/30+60/60=2,7
φ(B)=500/900+30/20+40/60=2,25
A>B
Недостаток метода в том что он зависит от внешних альтернатив
Добавляем третью альтернативу.
Ai |
K1 |
K2 |
K3 |
A1 |
900 |
20 |
60 |
A2 |
500 |
30 |
40 |
A3 |
400 |
60 |
100 |
M1=900 M2=60 M3=100.
φ(A)=900/900+20/30+60/100=1,93
φ(B)=500/900+30/60+40/100=1,44
φ(C)=400/500+60/60+100/100=2,44
Типы многокритериальных задач:
1. Задано — множество альтернатив, множество критериев, множество оценок исходов.
В этом случае потребуется упорядочить альтернативы по качеству и выбрать лучшие,
путем построения решаюшего правила.
2. Задано — множество критериев, множество альтернатив. Сравнение альтернатив не
задано или задано частично. Требуется обощенное рещающее правило для
упорядочивания альтернатив.
Многокритериальные задачи принятия решений с субъективными моделями: типы, постановки. Этапы решения. Метод аналитической иерархии. Метод парных сравнений для многокритериальной оценки альтернатив: шкала отношений, матрицы парных сравнений; собственный вектор и собственные значения; определение наилучшей альтернативы.
Типы многокритериальных задач:
Задано — множество альтернатив, множество критериев, множество оценок исходов. В этом случае потребуется упорядочить альтернативы по качеству и выбрать лучшие, путем построения решающего правила.
Задано — множество критериев, множество альтернатив. Сравнение альтернатив не задано или задано частично. Требуется обобщённое решающее правило для упорядочивания альтернатив.
Метод анализа иерархий.
Этапы:
Построение дерева «цели-критерии-альтернативы»
Выполнение попарного сравнение элементов каждого уровня дерева.
Вычисление коэффициентов важности альтернатив, целей, критериев.
Построение решающего правила для оценки и классификации альтернатив.
Первый этап.

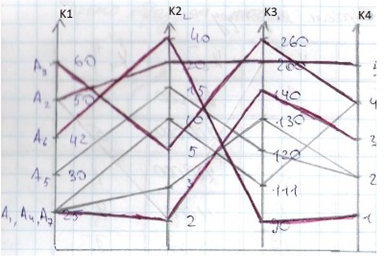
Матрица критериев.
 Если
Kji
— преимущество критерия Ki
над Kj
, то Kij
— обратная сторона.
Если
Kji
— преимущество критерия Ki
над Kj
, то Kij
— обратная сторона.
Суть метода попарного сравнения — для построения матрицы строится множество парных сравнений альтернатив(критериев).
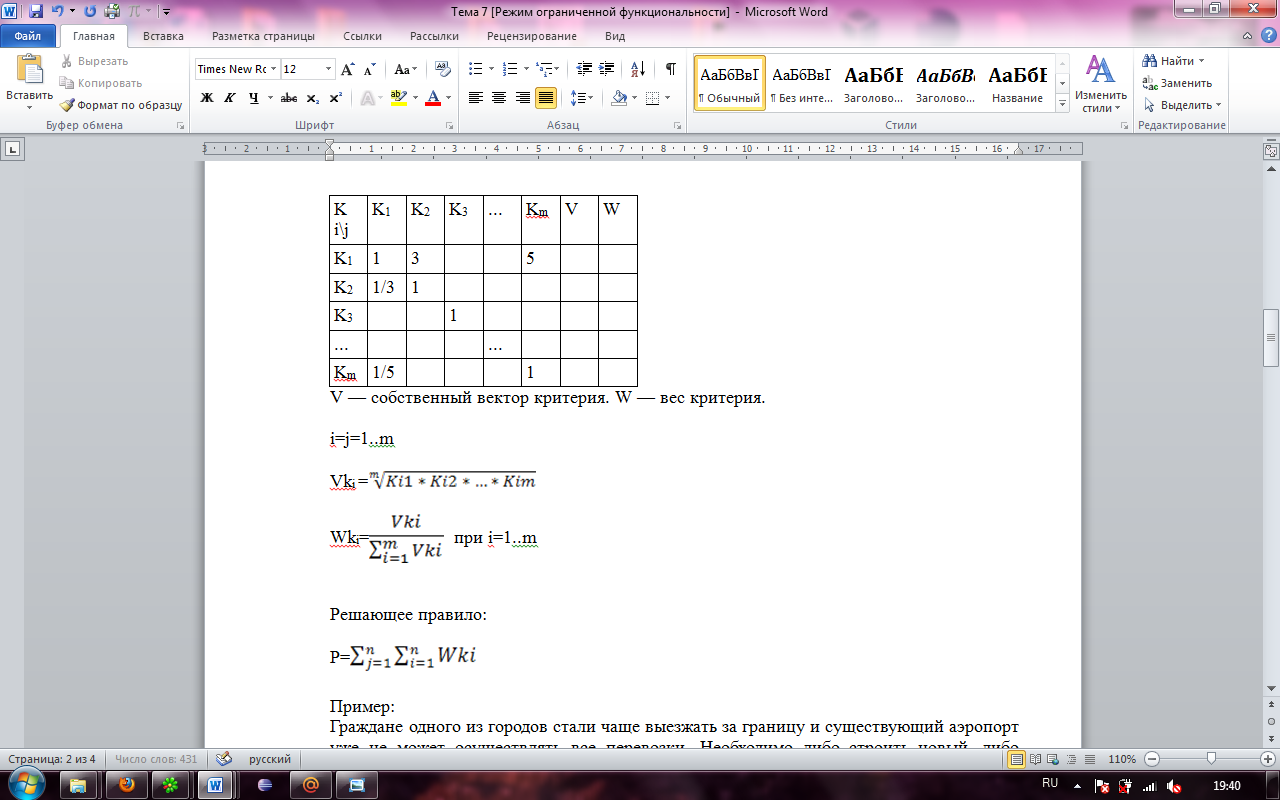
V — собственный вектор критерия. W — вес критерия.
i=j=1..m
Пример:
Граждане одного из городов стали чаще выезжать за границу и существующий аэропорт уже не может осуществлять все перевозки. Необходимо либо строить новый, либо модернизировать старый. Для строительства подобранно несколько площадок и определены критерии:
Стоимость проекта.
Расстояние от города
Шум
Дерево цели-критерии-альтернативы.
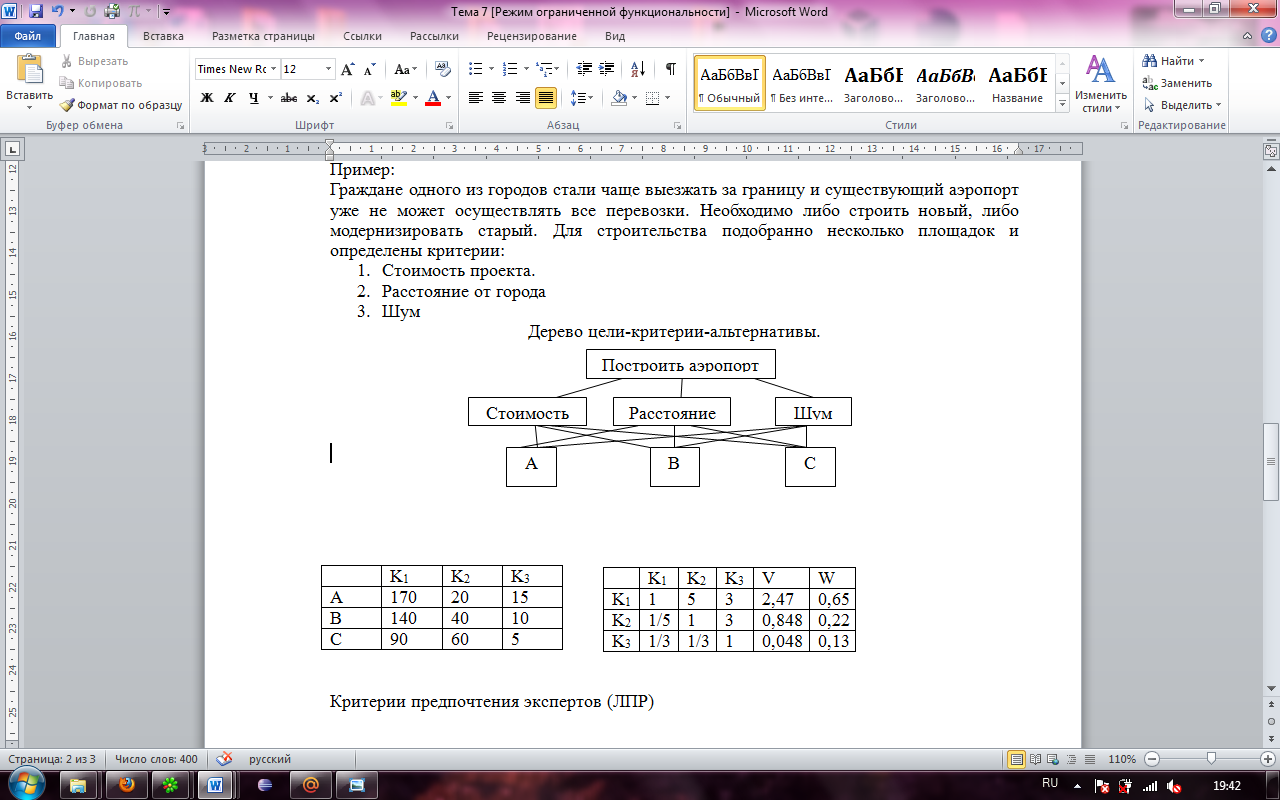
Критерии предпочтения экспертов (ЛПР)
V1
=
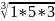 =2,47
=2,47
V1
=
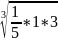 =0,848
=0,848
V1
=
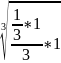 =0,048
=0,048
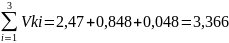
W1
=
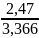 =0,65
=0,65
Матрица парных сравнений альтернатив по каждому из критериев.
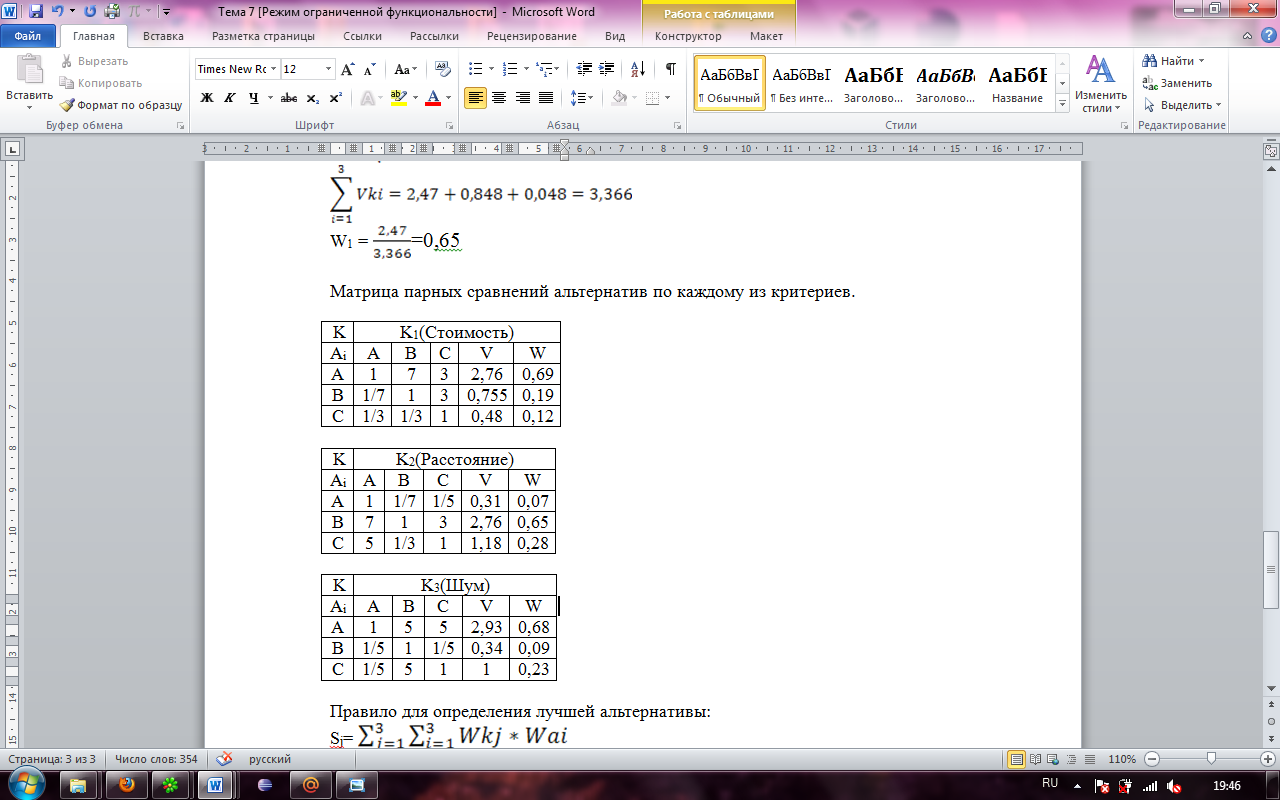
Правило для определения лучшей альтернативы:
Sj=
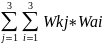
(вес критерия альтернативы * вес самой альтернативы)
Показатель качества:
SA=0,65*0,69+0,22*0,07+0,13*0,68=0,552
SB=0,65*0,19+0,22*0,65+0,13*0,09=0,278
SC=0,65*0,12+0,22*0,28+0,13*0,23=0,17
A является лучшей альтернативой.
Примечания.
В задаче оценивает один эксперт. Если же оценивает больше 1-3 экспертов то может быть:
Отбрасываются max и min, а от остальных считается среднее значение.
Самим экспертам дается рейтинг, на который умножается оценка эксперта.
Метод электре
Требования: должны быть заданы альтернативы. Определяется не количественный показатель качеств альтернатив, а устанавливается условие превосходства одной альтернативы над другой.
Дано:
Множество критериев: F={f1,…,fm}
Li – шкалы оценок
Веса критериев p={p1,…,pn} на бальной шкале
Ai (A1…An) – альтернативы
Требуется: выделить группу лучших альтернатив и упорядочить их.
Этапы решения
Этап 1.
На основании заданных оценок формируется fi(ai), fj(ak). Выделяются индекс согласия (cij) и индекс несогласия (dij) с гипотезой что «Альтернатива А лучше альтернативы В» (aj>ak)
Этап 2.
Задаются уровни согласия и несогласия для каждой пары альтернатив c, d.
Cij>=C, dij<=d
Если индекс согласия какой-то пары альтернатив CAB выше заданного, а индекс несогласия ниже заданного то считается, что альтернатива А лучше В. В противном случае альтернативы несравнимы.
Если оценки одинаковые – эквивалентные.
Этап 3.
Из множества альтернатив удаляются доминируемые. Оставщиеся образуют 1-ое ядро. Альтернативы входящие в это ядро могут быть эквивалентными либо несравнимыми.
Этап 4
Повышаем уровень согласия и понижаем уровень несогласия. Формируется новое ядро альтернатив.
Этап 5.
В последнее ядро, когда больше не надо понижать уровни согласия и несогласия, входят наилучшие альтернативы, а последовательность ядер упорядочивает альтернативы.
Пример:
Поставим каждому из m критериев вес (число, характеризующее важность этого критерия). Выдвинем гипотезу – «А лучше В».
Все критерии разбиваются на 3 категории:
p+ - подмножество критериев, по которым А предпочтительнее В.
p= - А равноценно В.
p- - В предпочтительнее А.
Формируем индекс согласия с гипотезой «А лучше В».
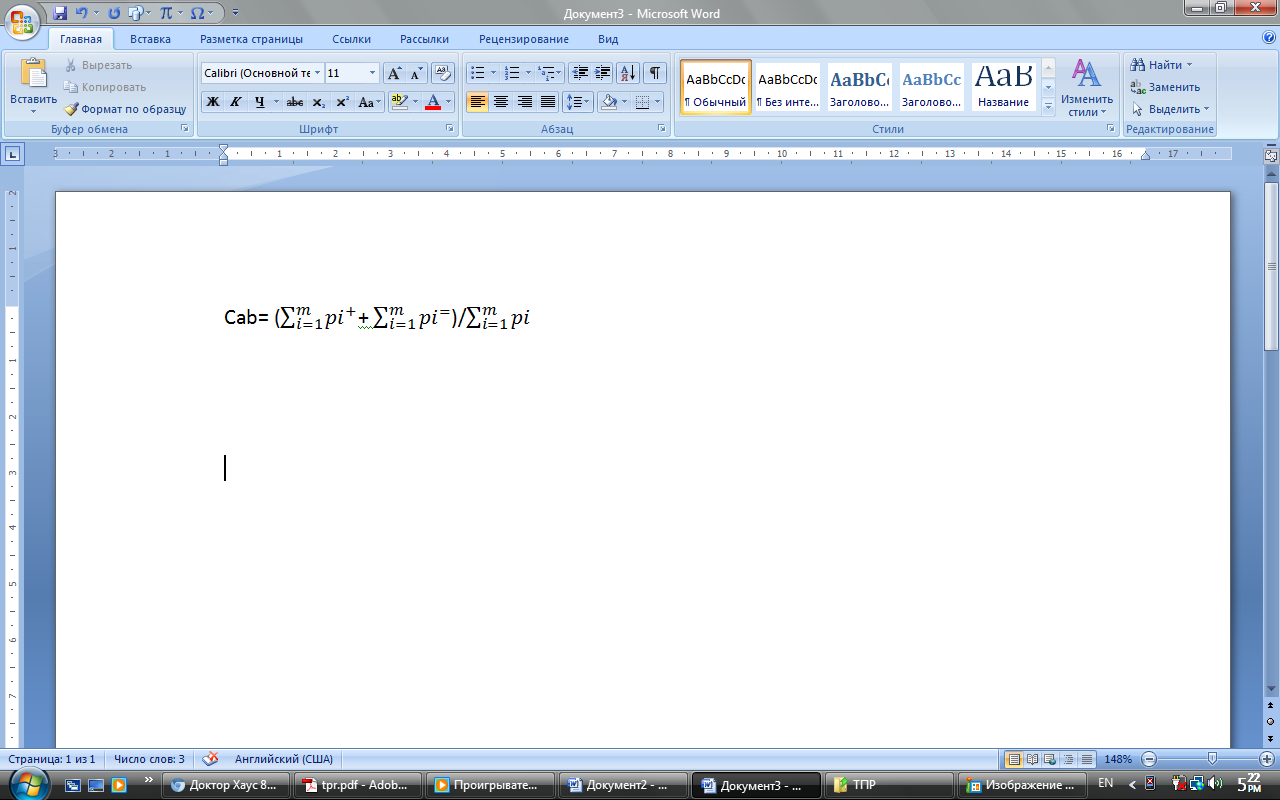 –
сумма
положительных критериев.
–
сумма
положительных критериев.
dAB определяется на основе самого противоречивого критерия, по которому В в наибольшей степени превосходит А. Чтобы учесть возможную разницу длин шкал критериев, разность оценок альтернатив А и В относят к длине наибольшей шкалы.
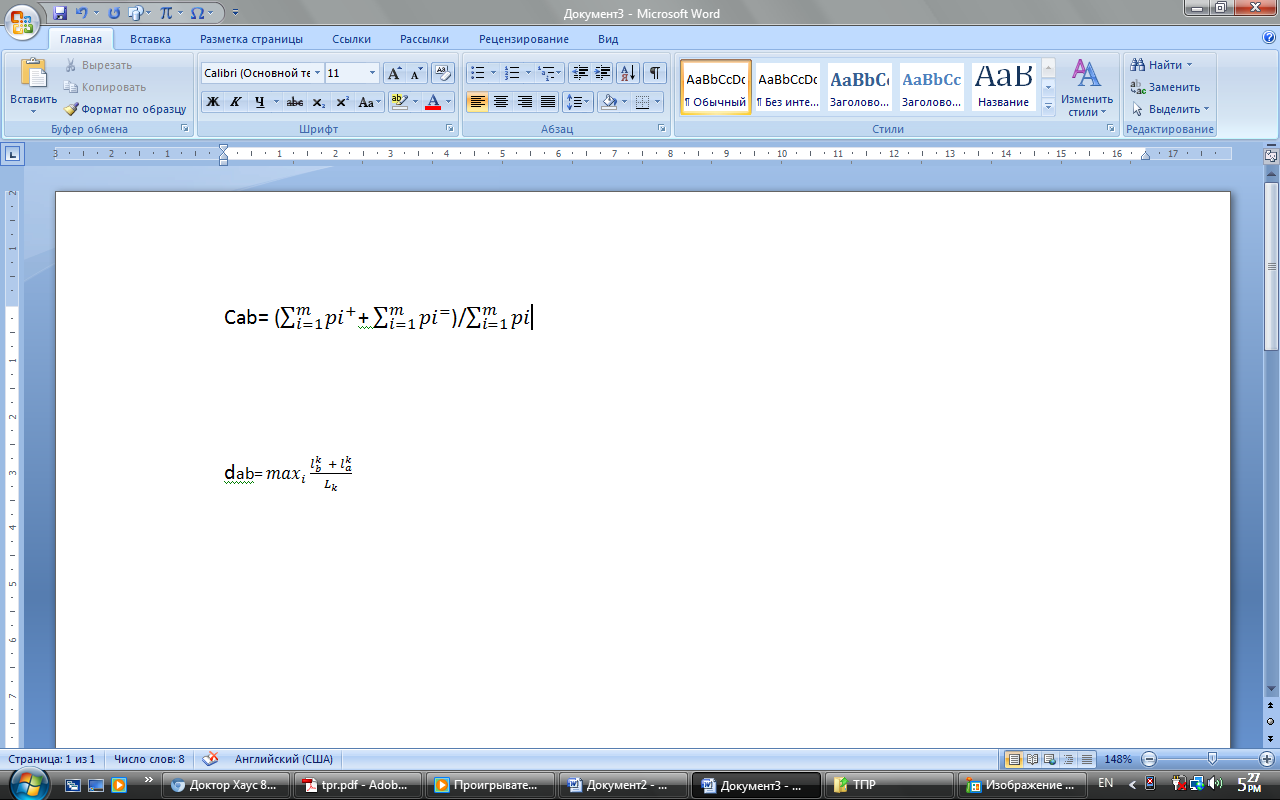
lbk Lak – оценки А и В по k критерию. Lk – длинна шкалы k критерия.
Свойства индекса согласия:
0≤ CAB ≤1
CAB =1 если p(=,+) - пусто
CAB сохраняет свое значение при замене одного критерия на несколько с одним и тем же весом.
Свойства индекса несогласия:
0≤ dAB ≤1
dAB сохраняет свое значение при введении более детальной шкалы по i-му критерию при тойже общей длине.
ЗЛП
Содержательная постановка задачи:
Некоторое предприятие, изучив рынок спроса и проведя его маркетинг, решило начать производство продуктов вида П1...Пn. Для их производства у предприятия были запасы ресурсов B1...Bn в количестве b1...bn. За каждую единицу проданной продукции предприятие получит прибыль С1...Сn.
Предприятию известна технологическая матрица затрат ресурсов каждого вида на производство продукции каждого вида.
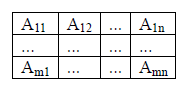
Aij – затраты I ресурса на производство единицы j продукции.
Необходимо найти такой план производства продукции который принесет максимальный доход предприятию от реализации всей произведенной продукции.
Формальная математическая модель:
Состав переменных.
X=(x1…xn) – план производства продукции
Xi – объем производства продукции I типа.
Целевая функция.
![]()
Система урованений(затраты)
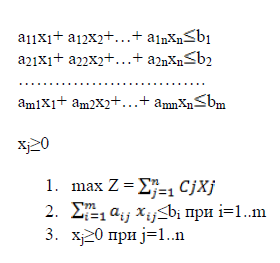
Задачи о смесях.
Произвести n видов продукции (x1…xn) из имеющихся ресурсов b1...bn но в каждом xj должно быть определенное количество ингредиентов.
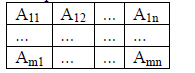
Количество ингредиентов каждого типа, затрачиваемое на производство продукта каждого типа.
Суммарное количество ≥ bi
Общая задача линейного программирования:
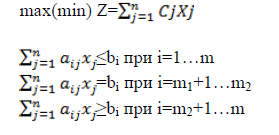
Формы записи ОЗЛП
Скалярная форма записи(↑)
Матричная форма.
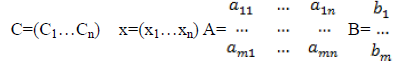
Векторная форма.

Каноническая форма.
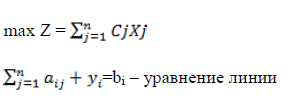
Симметричная форма
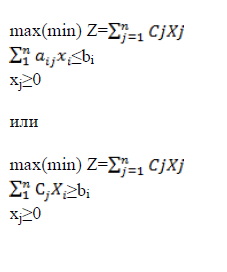
Различают
три основные формы задач линейного
программирование в зависимости от
наличия ограничений разного
типа.
Стандартная
задача ЛП.
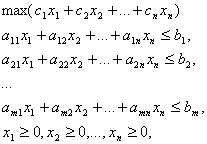 или,
в матричной записи,
или,
в матричной записи,
![]() где
где
![]() —
матрица коэффициентов. Вектор
—
матрица коэффициентов. Вектор
![]() называется
вектором коэффициентов линейной формы,
называется
вектором коэффициентов линейной формы,
![]() —
вектором ограничений.
Стандартная
задача важна ввиду наличия большого
числа прикладных моделей, сводящихся
наиболее естественным образом к этому
классу задач ЛП.
Каноническая
задача ЛП.
—
вектором ограничений.
Стандартная
задача важна ввиду наличия большого
числа прикладных моделей, сводящихся
наиболее естественным образом к этому
классу задач ЛП.
Каноническая
задача ЛП.
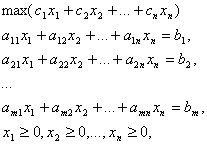 или,
в матричной записи,
или,
в матричной записи,
![]() Основные
вычислительные схемы решения задач ЛП
разработаны именно для канонической
задачи.
Общая
задача ЛП.
В
этой задачи часть ограничений носит
характер неравенств, а часть является
уравнениями. Кроме того, не на все
переменные наложено условие
неотрицательности:
Основные
вычислительные схемы решения задач ЛП
разработаны именно для канонической
задачи.
Общая
задача ЛП.
В
этой задачи часть ограничений носит
характер неравенств, а часть является
уравнениями. Кроме того, не на все
переменные наложено условие
неотрицательности:
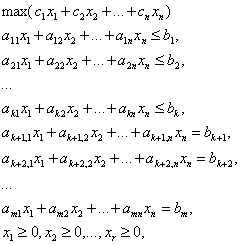 Здесь
Здесь
![]() .
Ясно, что стандартная задача получается
как частный случай общей при
.
Ясно, что стандартная задача получается
как частный случай общей при
![]() ;
каноническая — при
;
каноническая — при
![]() .
Все
три перечисленные задачи эквивалентны
в том смысле, что каждую из них можно
простыми преобразованиями привести к
любой из двух остальных.
При
изучении задач ЛП сложилась определенная
терминалогия. Линейная форма
.
Все
три перечисленные задачи эквивалентны
в том смысле, что каждую из них можно
простыми преобразованиями привести к
любой из двух остальных.
При
изучении задач ЛП сложилась определенная
терминалогия. Линейная форма
![]() ,
подлежащая максимизации (или минимизации)
, называется целевой функцией. Вектор
,
подлежащая максимизации (или минимизации)
, называется целевой функцией. Вектор
![]() ,
удовлетворяющий всем ограничениям
задачи ЛП, называется допустимым
вектором, или планом. Задача ЛП, для
которой существуют допустимые векторы,
называется допустимой задачей. Допустимый
вектор
,
удовлетворяющий всем ограничениям
задачи ЛП, называется допустимым
вектором, или планом. Задача ЛП, для
которой существуют допустимые векторы,
называется допустимой задачей. Допустимый
вектор
![]() ,
доставляющий наибольшее значение
целевой функции по сравнению с любым
другим допустимым вектором
,
доставляющий наибольшее значение
целевой функции по сравнению с любым
другим допустимым вектором
![]() ,
т.е.
,
т.е.
![]() ,
называется решением задачи, или
оптимальным планом. Максимальное
значение
,
называется решением задачи, или
оптимальным планом. Максимальное
значение
![]() целевой
функции называется значением задачи.
целевой
функции называется значением задачи.
Симметричная форма записи задачи линейного программирования. Здесь принято выделять две стандартные задачи − задачу максимизации и задачу минимизации.
3.1. Стандартная задача максимизации: необходимо найти максимальное значение целевой функции (4.1) при ограничениях
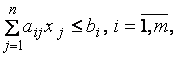
и условиях неотрицательности (4.2).
3.2. Стандартная задача минимизации: необходимо найти минимальное значение целевой функции (4.1) при ограничениях
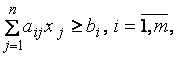
и условиях неотрицательности (4.2).
Общая форма записи задачи линейного программирования: необходимо найти экстремальное значение целевой функции
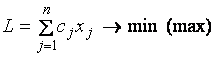 (4.1)
(4.1)
при ограничениях

на некоторые неизвестные могут быть наложены условия неотрицательности:
![]()
Здесь (и везде далее)
![]() заданные
числа
заданные
числа
![]()
Пример задач ЗЛП здесь:
Свойства
Множество всех планов задачи линейного программирования выпукло ( если оно не пусто).
Целевая функция задачи линейного программирования достигает своего минимального (максимального) значения в угловой точке многогранника решений. Если целевая функция принимает минимальное (максимальное) значение более чем в одной угловой точке, то она достигает того же значения в любой точке, являющейся выпуклой линейной комбинацией этих точек.
Если – угловая точка многогранника решений, то векторы , соответствующие положительным в разложении (10.14), линейно независимы.
. Геометрическая интерпретация и метод графического решения ЗЛП. Исследование области допустимых решений ЗЛП. Исследование решения на чувствительность.
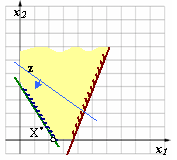
Дадим геометрическую интерпретацию задачи ЛП на примере задачи ЛП с двумя переменными. Каждое из неравенств задачи ЛП (1.2) определяет на координатной плоскости некоторую полуплоскость, а система неравенств в целом - пересечение соответствующих плоскостей. Множество точек пересечения данных полуплоскостей является областью допустимых решений (ОДР). ОДР всегда представляет собой выпуклым множеством, т.е. обладающим следующим свойством: если две точки А и В принадлежат этому множеству, то и весь отрезок, соединяющий точки А и В принадлежит ему. ОДР графически может быть представлена выпуклым многоугольником, неограниченной выпуклой многоугольной областью, отрезком, лучом, одной точкой. В случае несовместности системы ограничений задачи (1.2) ОДР является пустым множеством.
Целевая функция z(x)= c1x1 + c2x2 при фиксированном значении z(x) = L определяет на плоскости прямую линию c1x1 + c2x2 = L. Изменяя значения L, мы получим семейство параллельных прямых, называемых линиями уровня.
Прямые параллельны, потому что изменение значения L влечет изменение лишь длин отрезков, отсекаемых линией уровня на осях, а угловой коэффициент прямой tga =-c1/c2 останется постоянным (см. рис. 2.3). Поэтому для решения будет достаточно построить одну из линий уровня, произвольно выбрав значение L.
Напомним,
что линии уровня характеризуются тем,
что во всех точках одной линии уровня
значения функции z(x) равны между собой.
Градиентом
функции f(x)
=
![]() называется
вектор частных производных этой функции.
называется
вектор частных производных этой функции.
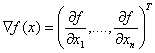
Градиент указывает направление наиболее быстрого возрастания функции и ориентирован перпендикулярно линиям уровня. Для линейной функции двух переменных линия уровня представляет собой прямую, перпендикулярную вектору , который служит градиентом данной функции. Следовательно, если линия уровня определяется уравнением f (x)= c1x1 + c2x2 = const , то этот вектор имеет вид (2.1) и указывает направление возрастания функции.
![]() (2.4)
(2.4)
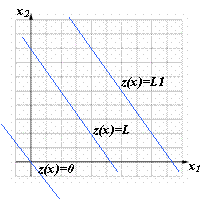
Рисунок 2.3 – Линии уровня целевой функции
Таким образом, геометрически отыскание оптимального решения – это нахождение такой точки ОДР, через которую проходит линия уровня ЦФ zmax (zmin), соответствующая наибольшему (наименьшему) значению функции z(x). Оптимальное решение всегда находится в крайней точке многоугольника ОДР, через которую пройдет целевая прямая, или на всей его стороне.
При поиске оптимального решения задач ЛП возможны исходы, описанные в таблице 2.1.
Таблица 2.1 - Возможные исходы решения задач ЛП
№ |
Ситуация |
1 |
С В этом случае вычисляются координаты оптимальной точки x1 и x2 , значение целевой функции в этой точке. Ответ записывается в следующей форме: Ответ:
|
2 |
Существует
бесконечное множество решений. Такая
ситуация возникает, когда прямая ЦФ
z параллельна ребру многоугольника,
образующего ОДР. Все точки, лежащие
на этом ребре имеют одинаковое значение
ЦФ. В Можно рассчитать координаты вектора y для какого-то конкретного l из интервала [0,1] и убедиться, что значение целевой функции для данной точки также равно z(x*) и z(x**). |
3 |
Н Если ОДР не ограничена в направлении оптимума целевой функции, то задача ЛП не имеет решений (см. рисунок справа). Ответ: задача ЛП не имеет решений вследствие неограниченности ЦФ на ОДР
Примечание: неограниченность ОДР в общем случае не означает отсутствие решений. Если бы в приведенном примере направление целевой функции было противоположное, то задача имела бы единственное решение (см. рисунок слева). |
4 |
Н Если ограничения задачи несовместны, т.е. ОДР – это пустое множество (D=Æ), то задача не имеет допустимых решений, а следовательно и оптимальных.
Ответ: задача ЛП не имеет решений вследствие несовместности ограничений. |
Графический метод довольно прост и нагляден для решения задач линейного программирования с двумя переменными. Он основан на геометрическом представлении допустимых решений и ЦФ задачи.
Каждое
из неравенств задачи линейного
программирования (1.2) определяет на
координатной плоскости
![]() некоторую
полуплоскость (рис.2.1), а система неравенств
в целом – пересечение соответствующих
плоскостей. Множество точек пересечения
данных полуплоскостей называется
областью
допустимых решений
(ОДР). ОДР всегда представляет собой
выпуклую
фигуру, т.е.
обладающую следующим свойством: если
две точки А и В принадлежат этой фигуре,
то и весь отрезок АВ принадлежит ей. ОДР
графически может быть представлена
выпуклым многоугольником, неограниченной
выпуклой многоугольной областью,
отрезком, лучом, одной точкой. В случае
несовместности системы ограничений
задачи (1.2) ОДР является пустым множеством.
некоторую
полуплоскость (рис.2.1), а система неравенств
в целом – пересечение соответствующих
плоскостей. Множество точек пересечения
данных полуплоскостей называется
областью
допустимых решений
(ОДР). ОДР всегда представляет собой
выпуклую
фигуру, т.е.
обладающую следующим свойством: если
две точки А и В принадлежат этой фигуре,
то и весь отрезок АВ принадлежит ей. ОДР
графически может быть представлена
выпуклым многоугольником, неограниченной
выпуклой многоугольной областью,
отрезком, лучом, одной точкой. В случае
несовместности системы ограничений
задачи (1.2) ОДР является пустым множеством.
Все вышесказанное относится и к случаю, когда система ограничений (1.2) включает равенства, поскольку любое равенство
![]()
можно представить в виде системы двух неравенств (см. рис.2.1)
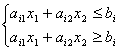
ЦФ
![]() при
фиксированном значении
при
фиксированном значении
![]() определяет
на плоскости прямую линию
определяет
на плоскости прямую линию
![]() .
Изменяя значения L, мы получим семейство
параллельных прямых, называемых линиями
уровня.
.
Изменяя значения L, мы получим семейство
параллельных прямых, называемых линиями
уровня.
Это
связано с тем, что изменение значения
L повлечет изменение лишь длины отрезка,
отсекаемого линией уровня на оси
![]() (начальная
ордината), а угловой коэффициент прямой
(начальная
ордината), а угловой коэффициент прямой
![]() останется
постоянным (см.рис.2.1). Поэтому для решения
будет достаточно построить одну из
линий уровня, произвольно выбрав значение
L.
останется
постоянным (см.рис.2.1). Поэтому для решения
будет достаточно построить одну из
линий уровня, произвольно выбрав значение
L.
Вектор
![]() с
координатами из коэффициентов ЦФ при
с
координатами из коэффициентов ЦФ при
![]() и
и
![]() перпендикулярен
к каждой из линий уровня (см. рис.2.1).
Направление вектора
перпендикулярен
к каждой из линий уровня (см. рис.2.1).
Направление вектора
![]() совпадает
с направлением
возрастания
ЦФ, что является важным моментом для
решения задач. Направление
убывания
ЦФ противоположно направлению вектора
.
совпадает
с направлением
возрастания
ЦФ, что является важным моментом для
решения задач. Направление
убывания
ЦФ противоположно направлению вектора
.
Суть
графического метода заключается в
следующем. По направлению (против
направления) вектора
в
ОДР производится поиск оптимальной
точки ![]() .
Оптимальной считается точка, через
которую проходит линия уровня
.
Оптимальной считается точка, через
которую проходит линия уровня
![]() ,
соответствующая наибольшему (наименьшему)
значению функции
,
соответствующая наибольшему (наименьшему)
значению функции
![]() .
Оптимальное решение всегда находится
на границе ОДР, например, в последней
вершине многоугольника ОДР, через
которую пройдет целевая прямая, или на
всей его стороне.
.
Оптимальное решение всегда находится
на границе ОДР, например, в последней
вершине многоугольника ОДР, через
которую пройдет целевая прямая, или на
всей его стороне.
При поиске оптимального решения задач линейного программирования возможны следующие ситуации: существует единственное решение задачи; существует бесконечное множество решений (альтернативный оптиум); ЦФ не ограничена; область допустимых решений – единственная точка; задача не имеет решений.
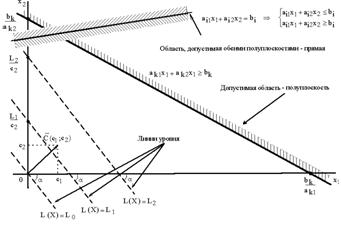
Рисунок 2.1 Геометрическая интерпретация ограничений и ЦФ задачи.
Методика решения задач ЛП графическим методом.
I. В ограничениях задачи (1.2) заменить знаки неравенств знаками точных равенств и построить соответствующие прямые.
II. Найти и заштриховать полуплоскости, разрешенные каждым из ограничений-неравенств задачи (1.2). Для этого нужно подставить в конкретное неравенство координаты какой-либо точки [например, (0;0)], и проверить истинность полученного неравенства.
Если неравенство истинное,
то надо заштриховать полуплоскость, содержащую данную точку;
иначе (неравенство ложное) надо заштриховать полуплоскость, не содержащую данную точку.
Поскольку
и
должны
быть неотрицательными, то их допустимые
значения всегда будут находиться выше
оси
![]() и
правее оси
,
т.е. в I-м квадранте.
и
правее оси
,
т.е. в I-м квадранте.
Ограничения-равенства разрешают только те точки, которые лежат на соответствующей прямой. Поэтому необходимо выделить на графике такие прямые.
III. Определить ОДР как часть плоскости, принадлежащую одновременно всем разрешенным областям, и выделить ее. При отсутствии ОДР задача не имеет решений.
IV.
Если ОДР – не пустое множество, то
нужно построить целевую прямую, т.е.
любую из линий уровня
(где
L – произвольное число, например,
кратное
![]() и
и
![]() ,
т.е. удобное для проведения расчетов).
Способ построения аналогичен построению
прямых ограничений.
,
т.е. удобное для проведения расчетов).
Способ построения аналогичен построению
прямых ограничений.
V.
Построить вектор
![]() ,
который начинается в точке (0;0) и
заканчивается в точке
,
который начинается в точке (0;0) и
заканчивается в точке
![]() .
Если целевая прямая и вектор
.
Если целевая прямая и вектор
![]() построены
верно, то они будут перпендикулярны.
построены
верно, то они будут перпендикулярны.
VI. При поиске максимума ЦФ необходимо передвигать целевую прямую в направлении вектора , при поиске минимума ЦФ – против направления вектора . Последняя по ходу движения вершина ОДР будет точкой максимума или минимума ЦФ. Если такой точки (точек) не существует, то можно сделать вывод о неограниченности ЦФ на множестве планов сверху (при поиске максимума) или снизу (при поиске минимум).
VII. Определить
координаты точки max (min) ЦФ
и
вычислить значение ЦФ
![]() .
Для вычисления координат оптимальной
точки
.
Для вычисления координат оптимальной
точки
![]() необходимо
решить систему уравнений прямых, на
пересечении которых находится
.
необходимо
решить систему уравнений прямых, на
пересечении которых находится
.
Исследование решения на чувствительность.
Неизбежное колебание значений таких экономических параметров, как цены на продукцию и сырье, запасы сырья, спрос на рынке и т.д. может привести к неоптимальности или непригодности прежнего режима работы. Для учета подобных ситуаций проводится анализ чувствительности, т.е. анализ того, как возможные изменения параметров исходной модели повлияют на полученное ранее оптимальное решение задачи ЛП.
Для решения задач анализа чувствительности ограничения линейной модели классифицируются следующим образом. Связывающие ограничения проходят через оптимальную точку. Несвязывающие ограничения не проходят через оптимальную точку. Аналогично ресурс, представляемый связывающим ограничением, называют дефицитным, а ресурс, представляемый несвязывающим ограничением – недефицитным. Ограничение называют избыточным в том случае, если его исключение не влияет на ОДР и, следовательно, на оптимальное решение. Выделяют следующие три задачи анализа на чувствительность.
1. Анализ сокращения или увеличения ресурсов:
·
на сколько можно увеличить (ограничения
типа ![]() )
запас дефицитного
ресурса для улучшения оптимального
значения ЦФ?
)
запас дефицитного
ресурса для улучшения оптимального
значения ЦФ?
· на сколько можно уменьшить (ограничения типа ) запас недефицитного ресурса при сохранении оптимального значения ЦФ?
2. Увеличение (ограничения типа ) запаса какого из ресурсов наиболее выгодно?
3. Анализ изменения коэффициентов ЦФ: каков диапазон изменения коэффициентов ЦФ, при котором не меняется оптимальное решение?
Симплексный метод решения ЗЛП: общая идея, построение плана решения ЗЛП, условие опорности плана, условие оптимальности опорного плана, алгоритм перехода к нехудшему опорному или оптимальному плану. Вырожденные ЗЛП.
Является методом целенаправленного перебора опорных решений задачи ЛП. Позволяет за конечное число шагов найти оптимальное решение или установить, что такое отсутствует.
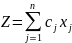
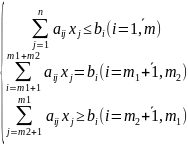
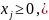
Приведем к каноническому виду:
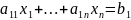

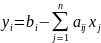
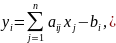
Заполним симплекс-матрицу:
-
- х1
- x2
…
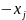
…
xn

Θ=min
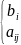
Y1
a11
a12
…
a1j
…
a1n
b1
b1/a1j
Y2
a21
a22
…
a2j
…
a2n
b2
b2/a2j
…
…
…
…
…
…
…
…
…
Yi
ai1
ai2
…
aij
…
ain
bi
bi/aij
…
…
…
…
…
…
…
…
…
Ym
am1
am2
…
amj
…
amn
bm
bm/amj
Z
-c1
-c2
…
-cj
…
cn
1 столбец таблицы – базовые переменные, 1 строка свободные переменные, последняя строка – строка целевой функции(индексная)
Является ли план опорным?
План является
опорным, если в нем значения перемнных
неотрицательны (bi
Является ли план оптимальным?
Для того, чтобы план был оптимальным необходимо и достаточно, чтобы все коэффициенты индексной строки были неотрицательны.
Если не оптимальный, то переходим к новому опорному плану:
Выбираем max элемент из индексной строки – соответствующий ему столбец ведущий
Выбираем min элемент из столбца индексного отношения (последний столбец) – соответствующая ему строка – ведущая.
На их пересечении – ведущий элемент.
Базовая переменная, отвечающая строке ведущего элемента должна быть переведена в свободные переменные, а свободная в базовые. Строится новая таблица, содержащая новое название базовых переменных.
-
- х1
- x2
…
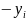
…
xn
B’
Y1
-a1j/aij
Y2
-a2j/aij
…
…
Xj
ai1/aij
ai2/aij
…
1/aij
…
ain/aij
bi/aij
…
…
Ym
-anj/aij
Z’
cj/aij
Остальные элементы:
Новый элемент = старый элемент – (элемент ведущей строки ведущего столбца * элемент ведущего столбца ведущей строки)/ведущий элемент.
Является план оптимальным? Нет -> переход к новому опорному плану согласно алгоритму.
Понятие двойственности позволяет унифицированным образом установить взаимосвязи для всех приѐмов и методов анализа модели на чувствительность. Основной идеей теории двойственности является то, что для каждой задачи линейного программирования существуют другие задачи линейного программирования, решение которых тесно связано с решением первой задачи.
В ряде книжек вместо термина прямая используется термин исходная, основная.
Прямая задача - состоит в нахождении максимального значения функции Y вида:
![]()
при ограничениях:
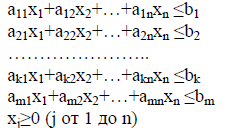
Двойственной по отношению к прямой задаче называется задача вида:
![]()
при условиях:
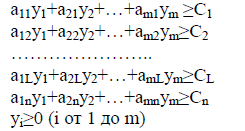
Эти задачи в линейном программировании называются двойственной парой.
Двойственная задача относительно исходной образуется следующим образом:
Целевая функция исходной задачи задаѐтся на максимум, а целевая функция двойственной задачи - на минимум.
Матрица коэффициентов исходной задачи имеет вид:

Матрица коэффициентов двойственной задачи будет являться транспонированной по отношению к матрице исходной задачи.

Число переменных двойственной задачи равно числу ограничений исходной задачи, а число ограничений двойственной задачи равно числу переменных исходной задачи.
Коэффициентами при неизвестных в целевой функции двойственной задачи являются свободные члены ограничений исходной задачи, а правыми частями ограничений двойственной задачи - коэффициенты при неизвестных целевой функции исходной задачи.
Если переменная Xj исходной задачи может принимать только лишь положительные значения, то j-е условие в двойственной задачи является неравенство вида ≥, если же переменная Xj может принимать как положительные, так и отрицательные значения, то j-ое ограничение двойственной задачи представляет собой равенство. Аналогичные связи существуют между ограничениями исходной задачи и переменными двойственной задачи. Если i-ое ограничение исходной задачи является неравенством, то i-ая переменная двойственной задачи yi ≥0, в противном случае yi может принимать как положительные, так и отрицательные значения.
Двойственные пары задач разделяют на симметричные и несимметричные.
В симметричной паре ограничения и прямой и двойственной задачи являются неравенствами вида ≥, т.е. переменные обеих задач могут принимать только неотрицательные значения.
Для практических целей рассмотренные правила позволяют составить следующую схему соответствия:
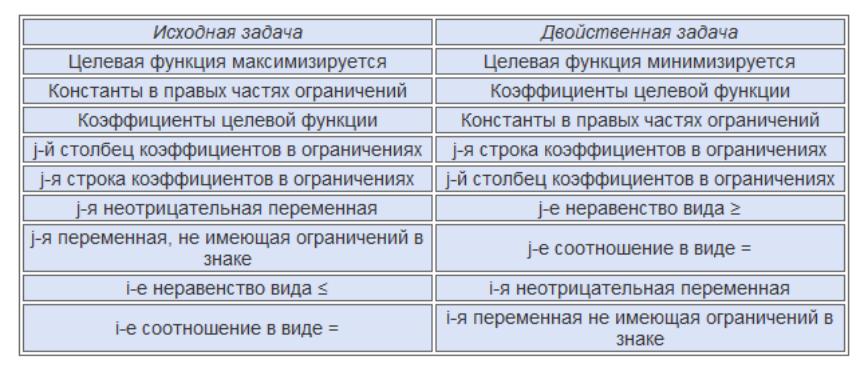
Экономический смысл двойственной задачи.
Если bi в прямой задаче избыточен то в двойственной bi будет иметь нулевую оценку. Если bi дефицитен то в двойственной задаче bi >0.
Двойственная задача:
![]()
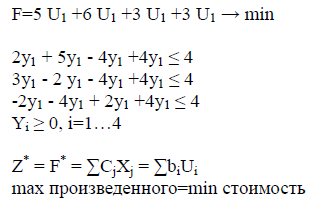
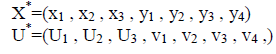
Если ресурс недефицитен то Ui = 0. Если ресурс дефицитен то Ui = const.
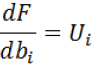
Цена единицы ресурса I типа

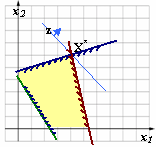 уществует
единственное решение задачи.
уществует
единственное решение задачи.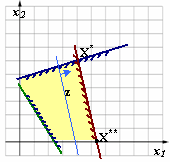 этом случае вычисляются координаты
концов отрезка x* и x**, а также значение
ЦФ в этих точках (они должны быть
равны). Ответ записывается в виде
выпуклой линейной комбинации концов
отрезка, на котором лежит множество
решений: Ответ:
этом случае вычисляются координаты
концов отрезка x* и x**, а также значение
ЦФ в этих точках (они должны быть
равны). Ответ записывается в виде
выпуклой линейной комбинации концов
отрезка, на котором лежит множество
решений: Ответ: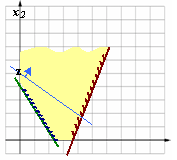 еограниченность
ЦФ на ОДР.
еограниченность
ЦФ на ОДР.
 есовместность
ограничений.
есовместность
ограничений.