9. Транспортная задача с ограничениями на пропускную способность (решение транспортной задачи с ограничениями?).

Транспортная задача с ограниченными пропускными спосо6ностями коммуникаций решается с дополнительным ограничением: , где d_ij - пропускная способность звена (i, j) в единицу времени. Математическая модель задачи такова:

,

при ограничениях

Эта задача разрешима при выполнении условий

.

Для транспортной задачи с ограниченными пропускными способностями справедливы следующие условия оптимальности полученного решения:

Принятие решений в условиях неопределённости и риска. Риск и его измерение. Матричные игры с нулевой суммой. Смешанные стратегии и их свойства. Статистические игры: постановка задачи; критерии принятия решений Байеса, Лапласа, Вальда, Сэвиджа, Гурвица. Примеры задач. Приведение матричной игры к ЗЛП (задаче линейного программирования).

Матричные игры с нулевой суммой.

Игра — это совокупность строго определенных правил, выполнение которых приводит обязательно к результату — выигрышу или проигрышу. Ход — частичная реализация правил. Стратегия — это выбор определенной линии поведения. Риск — угроза потери части или всего имеющегося ресурса. Риски бывают:

1. Финансовые.

2. Производственные.

3. Ресурсные.

4. и так далее.

Риски по характеру могут быть статические и динамические. Статические не меняются в процессе самой игры. Динамические соответственно наоборот.

Классификация игр:

1. По числу игроков — парные, для N-игроков.

2. По отношению между игроками — коалиционные, кооперативные, бескоалиционные, конфликтные и бесконфликтные.

3. По числу ходов — одношаговые и многошаговые.

4. По числу стратегий — конечное число стратегий и бесконечное.

5. И так далее.

Математическая постановка задачи.

1...N — игроки. V — выигрыш или проигрыш. V>0 – выигрыш, V<0 – проигрыш.

V₁+V₂ =0 — Игра с нулевой суммой. Если 1 игрок выигрывает, то остальные проигрывают — V₁=-V₂

Для двух игроков игра задается матрицей выигрышей или проигрышей. Предполагается что каждый игрок обладает своими стратегиями игры(количество строк и столбцов в матрице).

Стратегии игроков.

A={A1.......An}

B={B1........Bm}

Пересечение — проигрыш или выигрыш игрока A.

	B1	...	Bm
A1	a11		a1m
...
An	an1	…	anm

Существуют 2 стратегии поведения — максимальная стратегия из минимальных(по выигрышу). Оптимальной стратегией поведения будет стратегия, которая гарантирует максимальную прибыль от выигрыша. Это нижняя чистая цена игры. Игрок B постарается минимизировать свой проигрыш. Таким образом, стратегия игрока B — верхняя чистая цена игры. Каждый игрок может воспользоваться только одной стратегией.

α=β — улучшить результат нельзя.

α<β — улучшить результаты игры можно.

Пример:

Есть две воюющие стороны. Одна сторона обладает орудиями трех типов. Вторая сторона имеет самолеты трех типов. Каждая из сторон стремится минимизировать свой ущерб.

Против самолетов 1го типа эффективность средств ПВО будет (0.3,0.5,0.2)

Против самолетов 2го типа эффективность средств ПВО будет (0.1,0.6,0.4)

Против самолетов 3го типа эффективность средств ПВО будет (0.7,0.2,0.1)

Требуется определить наилучшие стратегии поведения этих двух сторон. Придать данной задаче игровую форму.

	B1	B2	B3
A1	0.3	0.5	0.2	0,2
A2	0.1	0.6	0.4	0,1
A3	0.7	0.2	0.1	0,1
	0,7	0,6	0,4

Находим оптимальную стратегию для первого игрока.

Α=0,2 β=0,4

Смешанные стратегии.

При смешанных стратегиях выигрыш может находится в интервале от α до β. Смешанная стратегия задается векторами Pi(вероятность использования стратегий для первого игрока) и Q(вероятность использования стратегий для второго игрока). В этом случае сам выигрыш является функцией стратегий и векторов вероятности использования этих стратегий.

Для того чтобы смешанная стратегия игроков A и B ,была оптимальной необходимо и достаточно чтобы цена игры была в интервале между верхней и нижней ценой.

p*={p₁....p_m}

q*={q_1......q_n}

α<V<β

Сведение задачи смешанной стратегии к ЗЛП.

Оптимальная стратегия игрока А обеспечивает ему средний выигрыш не меньший, чем цена игры v, при любой стратегии игрока В и выигрыш, равный цене игры, при оптимальной стратегии игрока В. Аналогично оптимальная стратегия В обеспечивает средний проигрыш (а для А выигрыш) не меньший чем цена игры и равный ей, если А использует оптимальную стратегию.

Это можно записать так:

a₁₁p₁+a₂₁ p₂+...a_n1p_n=>V

a₁₂p₁+a₂₂ p₂+...a_n2p_n=>V

...

a_1mp₁+a_2m p₂+...a_nmp_n=>V

p₁+...+p_n=1 //сумма всех вероятностей =1

a₁₁q₁+....+a_1mq_m=<V

….......................

a_m1q₁+....+a_mnq_n=<V

q₁+...+q_m=1

Разделив каждое из неравенств на V получим следующую систему:

G_i = p_i/V

a₁₁G₁+a₂₁ G₂+...a_n1 G_n=>1

a₁₂G₁+a₂₂ G₂+...a_n2 G_n=>1

...

a_1mG₁+a₂₂ G₁+...a_nm G_n=>1

При этом целевая функция примет вид G₁+G₂+…+G_n = 1/V. Максимизация цены V эквивалента минимизации 1/V, поэтому задача может быть сформулирована следующим образом: определить значения переменных G_i >0 i=1…n так чтобы они удовлетворяли линейным ограничениям(полученной системе уравнений) и при этом линейная функция G₁+G₂+…+G_n = Z обращалась в минимум.

Это задача линейного программирования. Решая эту задачу, мы получим оптимальное решение p*_{1 ,} p*_{2 , …,} p*_n и оптимальную стратегию S*_a.

Статистические игры (игры с природой)

Подвид игр, в котором мы не знаем, как ведёт себя второй игрок. Будем считать его природой (средой). Игра также задаётся платёжной матрицей, где вместо стратегий игрока В у нас будут состояния природы Sj.

	S1	S2	S3	…	Sm
A1	A11
A2
An
Q	Q1	Q2	Q3

Qj – вероятность нахождения в состоянии j

Критерий Байеса:

Применяется, если известны значения q1..qm. В качестве оценки альтернативы используем её математическое ожидание:

B(i) =

Оптимальной по критерию Байеса является та альтернати­ва, которая максимизирует оценку B(i).

B=max B(i)=max , i=1..n

В случае когда величины вероятностей q1..qm неизвестны используют критерии Лапласа, Вальда, Сэвиджа и Гурвица.

Критерий Лапласа:

Основан на гипотезе равновозможности (равновероятности). При принятии данной гипотезы в качестве оценки i-й альтернативы выступает среднеарифметичес­кое выигрышей, стоящих в i-й строке матрицы выигрышей. Таким образом, оценка по критерию Лапласа имеет вид

L(i)=

Оптимальной по критерию Лапласа является та альтернати­ва, которая максимизирует оценку L.

L=max L(i)=max

Критерий Вальда

Основан на гипотезе антагонизма, кото­рая может быть сформулирована в следующем виде: «При выборе решения надо рассчитывать на самый худший возможный вари­ант»-

При принятии данной гипотезы оценкой альтернативы i слу­жит число W(i)=min aij, j=1..m (минимум в строке) и сравнение любых двух альтернатив производится по величине критерия W. Оптимальной в этом слу­чае является альтернатива, максимизирующая W, т.е. альтернатива i*, для которой выполняется условие

W = max W(i) = max min aij , i=1..n, j=1..m

Число W(i) характеризует гарантированный уровень аль­тернативы i (так как при выборе альтернативы i выигрыш прини­мающего решение — независимо от состояния среды — не может быть меньше, чем W(i)). Таким образом, принцип максимина основан на макисимизации минимального возможного (т. е. га­рантированного) выигрыша; поэтому иногда этот принцип назы­вают также принципом максимального гарантированного результата.

Критерий Гурвица

Связан с введением показателя 0 < альфа < 1, называемого показателем пессимизма. Гипотеза о поведении природы состоит в этом случае в том, что при любом выборе альтер­нативы наихудший для принимающего решения вариант реализу­ется с вероятностью а, а наилучший — с вероятностью 1-альфа. Тогда оценкой альтернативы г является взвешенная сумма

H(i) = альфа*min аij + (1-альфа)*max аij. i=1..n, j=1..m

При альфа = 1 этот критерий превращается в «критерий крайнего пессимизма» (т.е. в критерий Вальда), а при а = 0 — в крите­рий крайнего оптимизма.

Критерий Сэвиджа

Основан на преобразовании первоначаль­ной матрицы выигрышей А в матрицу R — матрицу рисков (матрицу сожалений). Риском при выборе альтернативы i в со­стоянии j называется число rij= bj - аij, где bj = max аij, i=1..n.

Для критерия Сэвиджа оптимальной, считается альтернатива, минимизирующая максимальный риск (т. е. здесь используется минимаксный критерий для матрицы сожалений).

S=min S(i)=min max rij , i=1..n,j=1..m. i* - оптимальная альтернатива

Метод динамического программирования: общая постановка.

Решает задачи с многошаговой структурой. Постановка задачи:

1. Рассмотрим области существования системы. Любая точка данной области является состоянием этой системы и описывается вектором x=(x1…xn). Необходимо провести систему из одной точки в другую, целевую. Если заданы начальное состояние системы и целевое состояние системы, то задача называется задачей с закрепленными концами. Задачей с незакрепленными концами будет задачи с отсутствующим начальным состоянием (задана область). Стратегия перевода – решение, переводящее систему из начального состояния в целевое. А последовательность этих переходов называется траекторией движения. Это системы без последствия.

2. Можно написать Xt+1=f(Xt,Ut+1); В каждый момент времени состояние определяется предыдущим состоянием и воздействием оказанным на это состоянием. При этом система может либо что- то приобрести или что-то потерять.

3. Zt=Z(Xt-1,Ut) → max(min)

4. В задаче требуется построить такую цепочку(вектор), который приносит минимальный доход Zt.

Особенности задач динамического программирования:

- применяются для систем , состояния которых описываются значениями координат переменной.

- любая точка пространства описывает состояние системы.

- состояние точки в любой момент является функцией

X1=f1(x0, u1),

где x0 – предыдущее состояние, u1 – управление(решение , принятое на этом этапе)

x2= f2(x1, u2)

……………………..

• Можно ввести целевую функцию(функцию прибыли, например)

• Задачи такого рода – задачи управления в фазовом пространстве (задача без последствия)

Критерий оптимальности : (целевая функция - аддитивная, т.е. записывается как сумма значений)

Принципы динамического программирования.

1. Принцип оптимальности. Оптимальная траектория перехода из некоторого начального состояния в целевое, есть сумма оптимальных траекторий движения на каждом из шагов. На систему могут накладываться ограничения которые и образуют область допустимых решений.

2. Принцип погружения. Природа задачи не меняется при изменении числа шагов по переходу системы из одного состояния в другое.

Класс задач — распределение ресурсов между N — предприятиями.

Содержательная постановка: некоторая корпорация содержит в свем составе N — предприятий. Корпорация решила модернизировать и реконструировать эти предприятия. И для этой цели было выделено Х0 ресурсов. Известна прибыль которую получит каждое предприятия при вложении в нее Хj ресурсов. Также предполагается что размер прибыли также зависит от выделяемого количества ресурсов. Предполагается также что прибыль получаемая каждым предприятием измеряется в одних и тех же единицах. Прибыль каждого предприятия не зависит от прибыли получаемой каждым предприятием. Требуется максимизировать суммарную прибыль.

Методы решения:

Система рекуррентных уравнений Беллмана.

Рассматриваем N шагов и Х ресурсов.

Xj — количество ресурсов выделяемое j — предприятию.

Введем условно оптимальные функции прибыли Fi(xj).

F0(0)

F1(Xj) — прибыль, получаемая одним предприятием от вложения Xj ресурсов.

F2(Xj) — прибыль получаемая двумя предприятиями.

И так далее до Fn(X) получаемой всеми предприятиями.

Fn(Xn) — при вложении всего имеющегося ресурса.

Zi(x) – прибыль i-го предприятия от распределения ему x ресурсов

Fj(0)=0

F1(x1)=Zj(x)

F2(x2)=max(Z2(X2)+F1(X-X2))

F3(x3)=max(Z3(X3)+F2(X-X3))

…

Fk-1(x)=max(Zk-1(Xk-1)+Fk-2(X-Xk-1))

Fk(x)=max(Zk(Xk)+Fk-1(X-Xk))

Fn(X)=max(Zn(Xn)+Fn-1(X-Xn)

Fn(X0)=max(Zn(Xn)+Fn-1(X0-Xn)

Fn(X0) — максимальная прибыль

Решение:

Х1 … . . . . Х n

Схема решения задачи.

Сведение задачи распределения ресурсов к многоэтапной(N этапов по числу предприятий)

Х0 = KΔ (приводим к дискретной задаче)

 Х0 = KΔ Х = KΔ, k=0,1,2...m

 Fj(KΔ) j=1,...,N, k=0,1,2...m

Fj(0)=0;

F1(KΔ)=Zj(KΔ)

F2(KΔ)=max(Z2(KΔ)+F1(X0 -KΔ))

Решение задачи методом динамического программирования.

Исходные данные.

X	Z(X1)		Z(X2)			Z(X3)	X0=400
0	0		0			0	X0=4Δ
100	10		12			13	0<e<4
200	14		15			17	0<x<4Δ
300		20		18	19
400		30		35	40

X	F1(X)	F2(X)	F3(X)
0	0	0	0
100	10	12	13
200	14	22	25
300	20	26	35
400	30	35	40

F2(X)=max(Z2(X2)+F1(X-X2))

F2(100)=max(Z2(100)+F1(0)),(Z2(0)+F1(100))=max((12+0),(0+10))=12

F2(200)=max(Z2(200)+F1(0)),(Z2(100)+F1(100)),(Z2(0)+F1(200))=max((15+0),(12+10),(0+14))=22

F2(300)=max(Z2(300)+F1(0)),(Z2(200)+F1(100)),Z2(100)+F1(200),Z2(0)+F1(300)=max((18+0),(15+10),(12+14),(0+20))=26

F2(400)=max((Z2(400)+F1(0)),(Z2(300)+F1(100)),(Z2(200)+F1(200)),(Z2(100)+F1(300)),(Z2(0)+F1(400)))=max((35+0),(18+10),(15+14),(30+0))=35

F3(100)=max((Z3(100)+F2(0)),(Z3(0)+F2(100)))=max(12,13)=13

F3(200)=max((Z3(200)+F2(0)),(Z3(100)+F2(100)),(Z3(0)+F2(200)))=max((17-0),(13+12),(0+22))=25

F3(300)=max((Z3(300)+F2(0)),(Z3(200)+F2(100)),(Z3(100)+F2(200)),(Z3(0)+F2(300)))=max(19+0),(17+12),(13+22),(26)=35

F3(400)=max((Z3(400)+F2(0)),(Z3(300)+F2(100)),(Z3(200)+F2(200)),(Z3(100)+F2(300)),(Z3(0)+F3(400)))=max((40),(19+12),(17+22),(13+26),(35))=40

X3=400

X2=0

X1=0

Z=Z1(X1)+Z2(X2)+Z3(X3)=40

Дискретное программирование: задачи целочисленного и булевского программирования.

1. С задачами физической нелинейности

2. Задачи с двоичными переменными

Классы ЗДП:

1. Требование цело численности в явном виде не присутствует, но при целочисленных исходных данных решение тоже всегда целочисленное.

2. Задачи с неделимостями (т.е. в оптимальном плане переменные всегда целые)

3. Задачи с булевскими переменными. (о покрытии)

4. Задачи комбинаторного типа. (задача коммивояжёра)

Метод ветвей и границ.

Сущность метода: снимает условие цело численности. Если решение не цело-численное, формируется пара задач.

Постановка, математическая модель, алгоритм решения примеры.

Выделение целой части:

Строим 2 задачи:

1. 

2. решение продолжается пока не найдется значение цел.функции хуже чем у родительской.

Понятие о нелинейном программировании.

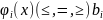
Если не линейны, т.е. вспухлые или выпуклые, имеют частные производные второго порядка. Имеет только частное решения.

Функция Лагранжа.

Для решения используется функция Лагранжа

Функция:

– множество Лагранжа.

При выполнении всех условий может быть найден глобальный мин и макс.

Схема алгоритма решения нелинейных задач.

1. Составим функцию Лагранжа

2. Найти частные производные по всем параметрам x, 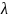, приравнять их к 0. Получить систему из (n+m) уравнений. Если возможно решаем эту задачу.

3. Из стационарных точек выбрать те в которых функция Z(x) ( ) ( и при ограничениях