Транспортная задача линейного программирования

Транспортная задача заключается в определении оптимального плана перевозок некоторого однородного груза из m пунктов отправления А₁, А₂, … , А_m в n пунктов потребления B_1, B_2,..., B_n.

Рассмотрим транспортную задачу, где в качестве критерия оптимальности является стоимость перевозок всего груза, которая должна быть минимальной.

Введем обозначения:

а_i – запасы груза в i-ом пункте отправления ( );

b_i – величина заказа на этот груз в j-ом пункте назначения

с_ij – стоимость перевозки единицы груза из A i-гo пункта отправления в В j-ый пункт потребления (тариф перевозок);

x_ij – количество груза, доставленного из i пункта в j пункт, х_ij≥0.

Определить план перевозок груза из пунктов отправления в пункты назначения так, чтобы: вывести все грузы от поставщиков; удовлетворить заявки каждого потребителя; обеспечить минимальные транспортные расходы на перевозку груза.

Все исходные данные транспортной задачи можно записать в виде транспортной таблицы 4.

где 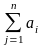- суммарный запас груза у поставщиков;

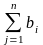- суммарная величина заявок потребителей

Математическая постановка транспортной задачи заключается в определении матрицы 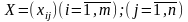; которая удовлетворяет следующим условиям:

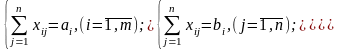
Таблица 4

Пункты от- правления	Пункты назначения						Запасы a1
	В1	В2	...	B1	...	Bn
A1	с11 x11	с12 x12	...	с1i x1i	...	с1n x1n		a1
А2	с21 x21	с22 x22	...	с1i x1i	...	с1n x1n		a2
...	…	…	...	…	…	…		…
Ai	сi1 xi1	сi2 xi2	...	сij xij	...	сin xin		ai
…	…	…	…	…	…	…		…
Аm	сm1 xm1	сm2 xm2	...	сmj xmj		сmn xmn		am
Заявки b1	b1	b2	…	bj	…	bn

И обеспечивает минимальное значение целевой функции

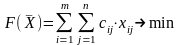
а) всякое неотрицательное решение системы линейных уравнений, определяемое матрицей ; называется допустимым планом транспортной задачи:

б) Ранг матрицы, составленный из коэффициентов при неизвестных системы линейных уравнений транспортной задачи, на единицу меньше числа уравнений, т.е. равен (m+n-1). Следователь-число линейно независимых уравнений равно (m+n-1), они образует базис, а соответствующие им (m+n-1) переменных будут являться базисными.

в) Допустимый план транспортной задачи, имеющий не более (m+n-1) отличных от нуля величин x_ij, называется опорным.

г) Если в опорном плане число отличных от нуля компонент равно в точности (m+n-1), то план является невырожденным, если меньше, то план называется вырожденным.

д) План . При котором функция 4 принимает свое минимальное значение, называется оптимальным планом транспортной задачи.

е) Для решения транспортной задачи необходимо и достаточно, чтобы суммарные запасы груза в пунктах отправления были равны сумме заявок пунктов назначения

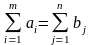
ж) Модель транспортной задачи, удовлетворяющая этому условию, называется закрытой. Если же указанное условие не выполняется, то модель называется открытой.

В случае превышения запаса над заявками: 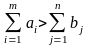вводится фиктивный (n+1) пункт назначения с потребностью 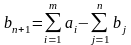и соответствующие тарифы считаются равными нулю:

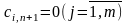
При 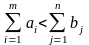вводится фиктивный (m+1) пункт отправления с запасом груза 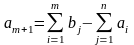, и тарифы принимаются равными нулю: .

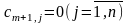Рассмотрим один из методов построение первого опорного плана - метод наименьших тарифов.

з) Наилучшим элементом матрицы тарифов называется наименьший тариф, если задача поставлена на минимум, наибольший тариф - если задача поставлена на максимум целевой функции.

Алгоритм построения первого опорного плана методом наименьшей стоимости включает следующие этапы.

1. Среди тарифов находится наименьший.

2. Клетку с выбранным тарифом заполняем максимально возможным объемом груза с учетом ограничений по строке и столбцу, при этом либо весь груз вывозится от соответствующего поставщика, либо полностью удовлетворяется заявка потребителя. Строка или столбец таблицы вычеркивается и в дальнейшем распределении не участвует.

3. Из оставшихся тарифов вновь находим наилучший, и процесс продолжается до тех пор, пока не будет распределен весь груз.

Если модель транспортной задачи открытая и введены фиктивный поставщик или потребитель, то распределение осуществляется сначала для действительных поставщиков и потребителей, и в последнюю очередь нераспределенный груз направляется от фиктивного поставщика или к фиктивному потребителю.

Дальнейшее улучшение первого опорного плана и получение оптимального плана производим методом потенциалов.

и) План X=(x_ij) транспортной задачи будет являться оптимальным, если существует система m+n чисел α_i, β_j называемых потенциалами, удовлетворяющая условиям:

α_i +β_j ≤ с_ij для занятых клеток, где x_ij>0

α_i + β_j ≤c_ij для свободных клеток, где х_ij=0

при решении задачи на минимум, а при решении задачи на максимум:

β_j – α_i =с_ij для занятых клеток, где x_ij>0

β_j – α_i ≥с_ij для свободных клеток, где х_ij=0

Потенциалы α_i и β_j являются переменными двойственной транспортной задачи и обозначают оценку единицы груза в пунктах отправления и назначения соответственно.

Введем обозначение оценки свободной клетки таблицы:

Δ_ij=c_ij–( α_i +β_j)

Если среди оценок Δ_ij нет отрицательной (задача поставлена на минимум), то опорный план является оптимальным и все свободные клетки потенциальны.

Алгоритм метода потенциалов включает следующие этапы.

1. Построение первого опорного плана.

2. Проверка вырожденности плана.

Потенциалы α_i и β_j могут быть рассчитаны только для невырожденного плана. Если число занятых клеток в опорном плане меньше, чем (m+n+1) . то вносим нуль в одну из свободных клеток таблицы так, чтобы общее число занятых клеток стало равным (m+n+1). Нуль вводят в клетку с наилучшим тарифом одного из одновременно вычеркиваемых рядов таблицы. При этом фиктивно занятая нулем клетка не должна образовывать замкнутого контура с другими клетками таблицы.

3. Определение значения функций цели путем суммирования произведений тарифов (удельных затрат) на объем перевозимого груза по всем занятым клеткам таблицы