1.Способы определения точек пересечения прямой с плоскостью, с гранной поверхностью.

Е сли прямая и плоскость не параллельны, то они пересекаются в точке, которая принадлежит как прямой, так и плоскости.

Определение точки пересечения прямой l с плоскостью ABC в общем случае выполняется в такой последовательности:

– через прямую проводят вспомогательную проецирующую плоскость, например, απ₂; ее след α" совпадает с фронтальной проекцией прямой;

– находят линию MN пересечения плоскостей α и ABC;

– фиксируют точку O пересечения прямой l и прямой MN (в данном варианте сначала определяется проекция O' ).

Видимость прямой l по отношению к плоскости ABC определена с помощью пар конкурирующих точек F и G, M и P .

2. Построение линии пересечения плоскости частного и общего положения, двух плоскостей общего положения.

Для построения линии пересечения двух плоскостей a и b необходимо найти две точки, N и M каждая из которых принадлежит обеим плоскостям. Для нахождения точек N и M можно воспользоваться следующим алгоритмом:

Общ+час: Спроецируем плоскости a и ABC на П1. Плоскость общего положения АВС проецируется на плоскость П1 в виде треугольника А1В1С1, а плоскость частного положения a - в виде прямой a1. На плоскости П1 прямая a1 и АВС пересекаются в точках K1 (K1 принадлежит А1В1) и N1 (N1 принадлежит А1C1). Если через точки K1 и N1 провести проецирующие прямые до пересечения с плоскостью АВС, то получатся две точки K (K принадлежит АВ) и N (N принадлежит АC). Соединив точки K и N, мы получим прямую KN. Прямая KN - линия пересечения плоскости a с плоскостью АВС.

Общего:

1)Взять две дополнительные плоскости частного положения 1ЧП и 2ЧП;

2)Определить линии пересечения плоскостей частного положения 1ЧП и 2ЧП с плоскостями

общего положения a и b с помощью метода, приведенного в предыдущем пункте;

3)Определить точки N и M пересечения полученных линий.

3.Перпендикулярные прямые. Привести пример определения расстояния от точки до прямой общего положения.

П ересекающиеся и скрещивающиеся прямые в пространстве могут располагаться в частности под прямым углом друг к другу. Если обе прямые – общего положения, то факт их перпендикулярности на чертеже не отражается: проекцией прямого угла будет тупой (острый) угол.

И только в случае, если одна из прямых параллельна плоскости проекций, прямой угол проецируется в натуральную величину на ту плоскость, которой прямая параллельна. Это предложение (теорема) является основополагающим для изображения на чертеже взаимно перпендикулярных прямых: тогда и только тогда прямой угол проецируется в натуральную величину, если хотя бы одна его сторона параллельна плоскости проекций, а следовательно, является или фронталью, или горизонталью.

Расстояние от точки до прямой определяется длиной перпендикуляра, опущенного из точки на прямую. Пусть необходимо определить расстояние от точки М до прямой а общего положения.

Ч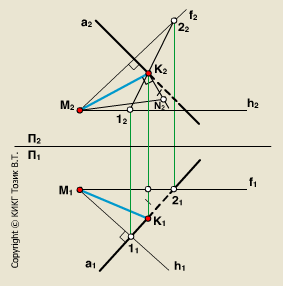 ерез заданную точку M проводится плоскость s перпендикулярная заданной прямой а. Плоскость задается двумя пересекающимися прямыми, фронталью (f) и горизонталью (h): s = h f.

Находится точка пересечения (K) исходной прямой а с плоскостью s.

Определяется расстояние от точки М до точки K способом прямоугольного треугольника. Длина гипотенузы прямоугольного треугольника M2K2N2 равна расстоянию от точки M до прямой а: |MK| = M2N2.

4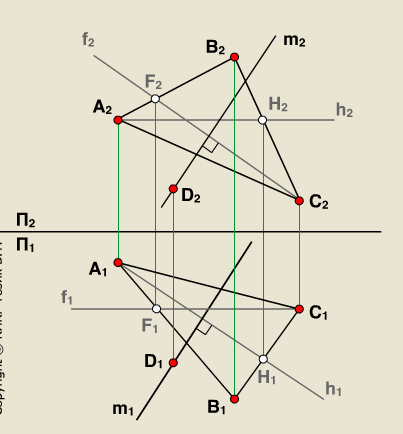 .Перпендикулярные прямая и плоскость. Привести примеры определения расстояния от точки до плоскости частного положения, от точки до плоскости общего положения. Привести пример построения перпендикуляра заданной длины к плоскости общего положения в точке, принадлежащей плоскости.

Прямая перпендикулярна плоскости если она перпендикулярна двум пересекающимся прямым этой плоскости.

Для того, чтобы прямая m была перпендикулярна плоскости , необходимо и достаточно, чтобы горизонтальная проекция прямой m₁ была горизонтальной проекции горизонтали (m₁ h₁), а фронтальная проекция прямой m₂ – фронтальной проекции фронтали (m₂ f₂).

Расстояние от точки до плоскости является длина перпендикуляр опущенного из данной точки к данной плоскости.

Д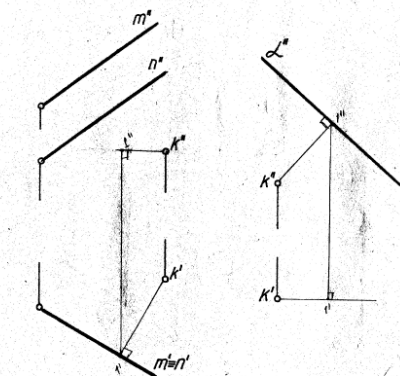 лину перпендикуляра можно определить с помощью прямоугольного треугольника.

Для построения перпендикуляра заданной длины для начала необходимо построить перпендикуляр произвольной длины, а затем увеличивая гипотенузу можно получить перпендикуляр заданной длины.

5.Перпендикулярные плоскости. Привести пример построения плоскости, перпендикулярной двум заданным плоскостям. Привести пример построения плоскости, параллельной заданной прямой и перпендикулярной заданной плоскости.

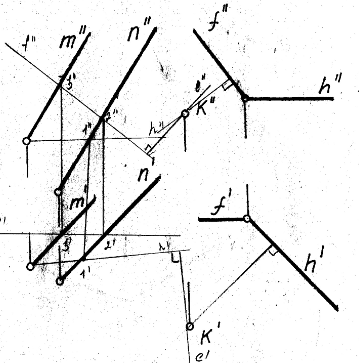Известно, что плоскости перпендикулярны, если одна из них проходит через перпендикуляр к другой.

Поэтому, построение плоскости, перпендикулярной данной, предполагает построение перпендикуляра к ней из любой точки, заведомо принадлежащей искомой плоскости.

Известно, что прямая параллельна плоскости, если она параллельна прямой, лежащей в плоскости. Например, прямая m параллельна прямой l, лежащей в плоскости