
- •1)Общая схема проверки гипотез
- •2) Постановка задачи адаптивного управления
- •1)Проверка гипотезы о математическом ожидании
- •1)Байесова теория принятия решений при непрерывных признаках
- •2)Подстройка параметров с использованием чувствительности
- •1) Идея классификации
- •2) Подстройка параметров динамических моделей с использованием итеративных моделей
- •Прямые методы восстановления решающей функции
- •1)Насыщенные планы. Симплекс.
- •1) Разбиение матрицы планирования на блоки
- •Адаптивные подстройки параметров не линейной статистической модели
- •1) Ортогональное планирование второго порядка
- •2) Простейший адаптивный алгоритм подстройки параметров
- •Метод случайного баланса
- •Многоэтапный метод селекции при построении моделей сложных объектов
- •Простейшие оценки плотности распределения и функции распределения.
- •Метод деления отрезка пополам при одномерном поиске унимодальных функций
- •2. Последовательный симплексный метод поиска экстремума функций
- •Оценка регрессии
- •Градиентный метод с использованием планирования первого порядка
- •Один из простых вариантов алгоритма Ньютона имеет вид
1)Байесова теория принятия решений при непрерывных признаках
Найдем
по формуле Байеса апостериорные
вероятности классов при условии измерения
признаков
 .
.
При распознавании выносим решение о том классе, для которого апостериорная вероятность больше (рис. 2.3.1):

если
 ,
то принимается 1-й класс;
,
то принимается 1-й класс;
если
 ,
то принимается 2-й класс.
,
то принимается 2-й класс.
Обобщение правила максимума апостериорной вероятности
 .
.
Для
двух классов .
.
2)Подстройка параметров с использованием чувствительности
Функции чувствительности
удовлетворяют уравнениям чувствительности
 ,
,

№10
1) Идея классификации

если P(1)*f(x|1) > P(2)*f(x|2) то принимается класс 1;
если P(1)*f(x|1) < P(2)*f(x|2), то принимается класс 2.

в
этом правиле классификации позволяет
получить для признака граничное значение
 ,
которое разбивает область изменения
признака на две подобласти
,
которое разбивает область изменения
признака на две подобласти
 и
.
Тогда решающее правило можно записать
в виде: если
,
то принимается класс 1, если
,
то принимается класс 2.
и
.
Тогда решающее правило можно записать
в виде: если
,
то принимается класс 1, если
,
то принимается класс 2.
2) Подстройка параметров динамических моделей с использованием итеративных моделей
 .
(7.3.1)
.
(7.3.1)
Используем
структуру оптимальной модели (7.3.1)
для построения итеративной модели.
Обозначим через
 выход модели в момент времени
при значениях параметров, вычисленных
в момент времени
выход модели в момент времени
при значениях параметров, вычисленных
в момент времени
 :
:
 ,
,
 .
(7.3.2)
.
(7.3.2)
Выход
модели в момент времени
 при значениях параметров, вычисленных
в момент времени
при значениях параметров, вычисленных
в момент времени
 ,
записывается в виде
,
записывается в виде

№11
Прямые методы восстановления решающей функции
Имеется обучающая выборка
|
|
Общего
объема
 .
Вводится фиктивная переменная
.
Вводится фиктивная переменная
 указывающая
на принадлежность к тому или иному
классу каждого выборочного значения
обучающей выборки. Например, для двух
классов
указывающая
на принадлежность к тому или иному
классу каждого выборочного значения
обучающей выборки. Например, для двух
классов

При параметрическом подходе задается уравнение решающей функции с точностью до параметров :
 ,
где
,
где
 – известные базисные функции, и из
некоторого критерия,
например из
критерия наименьших квадратов
– известные базисные функции, и из
некоторого критерия,
например из
критерия наименьших квадратов
,
вычисляются параметры
 решающей функции.
решающей функции.
недостатка вводятся более гладкие показатели качества классификации, например,
,

Простейший адаптивный алгоритм для динамической модели
Нелинейная
модель.
На каждом шаге линеаризуем модель и
приращения параметров отыскиваем из
равенства для линейного случая) выхода
модели и линеаризованной модели
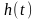 с
учетом критерия
с
учетом критерия
В итоге получаем алгоритм перестройки параметров нелинейной модели
 ,
,
 .
.
№12
1) построение линейной статической модели объекта
Уравнение линейной статической модели объекта имеет вид
 .
.
переход
от размерных входных переменных
 к безразмерным
:
.
В
новых безразмерных координатах
линейная модель также сохраняет вид:
с
параметрами
.
к безразмерным
:
.
В
новых безразмерных координатах
линейная модель также сохраняет вид:
с
параметрами
.
.
Параметры
 рассчитаем по критерию наименьших
квадратов
рассчитаем по критерию наименьших
квадратов
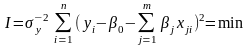 получаем
систему линейных алгебраических
уравнений:
получаем
систему линейных алгебраических
уравнений:
 .
.
,
где
 .
. .
.
2) Критерий наименьших квадратов
Если дисперсии различны, то измерения называются неравноточными. Тогда критерий наименьших квадратов имеет вид
 .
.
При
равноточных измерениях весовые
коэффициенты
![]() ,
характеризующие информативность
измерений, одинаковы
,
характеризующие информативность
измерений, одинаковы
![]() .
Тогда имеем
.
Тогда имеем
 .
.
Общий вид:
 .
.
№13
Полный факторный эксперимент. Движение по поверхности отклика
при
 можно рассчитать и коэффициент
можно рассчитать и коэффициент
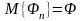 модели
модели .
.
Для этого в матрицу планирования вводим (для расчета ) столбец Новый столбец ортогонален к остальным. Тогда
,
, ,
,
 ,
.
,
.
Коэффициенты
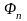 линейной модели являются оценками
составляющих градиента:
линейной модели являются оценками
составляющих градиента:
 .
Далее движение осуществляется по
поверхности отклика в направлении
оценки градиента:
.
.
Далее движение осуществляется по
поверхности отклика в направлении
оценки градиента:
.
Метод наименьших квадратов при линейной параметризации модели
Модель
объекта задана в виде линейной комбинации
известных (базисных) функций
 :
:
 ,
,
 .
.
Вектор-столбец
значений выхода модели (в моменты времени
 )
имеет вид
)
имеет вид
 .
(6.3.1)
Параметры
.
(6.3.1)
Параметры
 находим по критерию наименьших квадратов
находим по критерию наименьших квадратов

 .
.
№14
1) Дробные реплики
|
|
|
|
x3 |
1 |
+ |
+ |
+ |
+ |
2 |
– |
+ |
+ |
– |
3 |
+ |
– |
+ |
– |
4 |
– |
– |
+ |
+ |
5 |
+ |
+ |
– |
– |
6 |
– |
+ |
– |
+ |
7 |
+ |
– |
– |
+ |
8 |
– |
– |
– |
– |
необходимо
за основу взять полный факторный
эксперимент (например
)
и в качестве новой переменной (например
 )
взять один из столбцов, соответствующий
фактору взаимодействия (например
)
взять один из столбцов, соответствующий
фактору взаимодействия (например
 ).
Для данного примера дробная реплика
обозначается как
).
Для данного примера дробная реплика
обозначается как
 ,
генерирующим соотношением
,
генерирующим соотношением
 .
определяющий контраст
.
определяющий контраст
![]() .
.
№15

 ,
когда истинным является класс 1;
,
когда истинным является класс 1; ,
когда истинным является класс 2;
,
когда истинным является класс 2;