4.Чистловые характеристики закона распределения.

Математическое ожидание – случайной величины Х наз-ся его среднее значение вычисляемое по след. формулам - ф-ла может быть обоснована следующим примером:

Проводиться n опытов, в которых ,

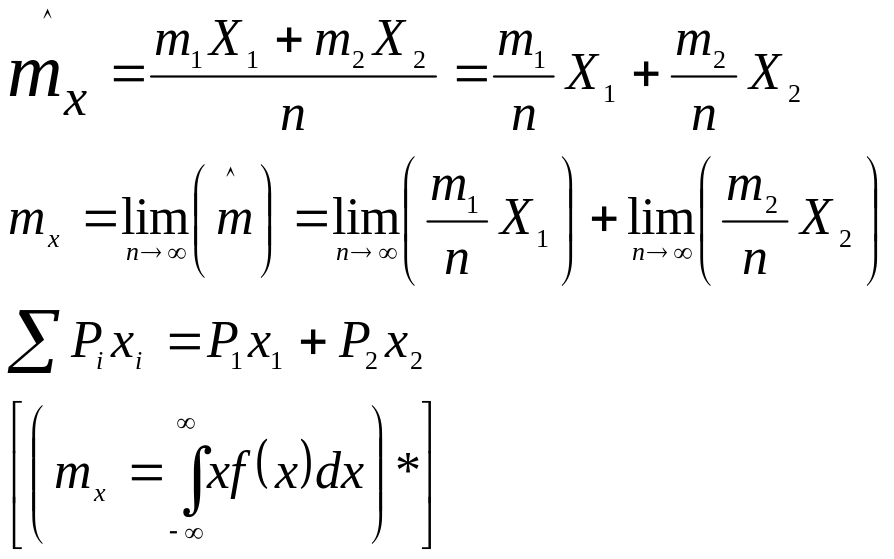
При математическом описании итогов опытов случ. величины подвергают случ. ожиданию.

Более общая числовая характеристика

- начальный момент -

- центр. момент

Центр. момент 2-го порядка:

Возможность дисперсии обусловлена тем, что она имеет смысл общей мощности.

12 Линейное преобразование случайных функций, заданных канноническими разложениями.

Случайная функция заданная в виде канонического выражения (*) легко подвергается произвольному линейному преобразованию:

Данное линейное преобразование тоже имеет вид канонического разложения

13 Стационарный случайный процесс

Очень часто в работающих системах их воздействие равномерно изменяется около среднего.

Такие процессы, средняя амплитуда которых и характер колебаний – const, называется стационарными.

Стационарный случайный процесс – процесс вероятностные характеристики, которого не меняются во времени.

1)

Данное требование не является существенным, потому что после операции центрирования оно выполняется автоматически.

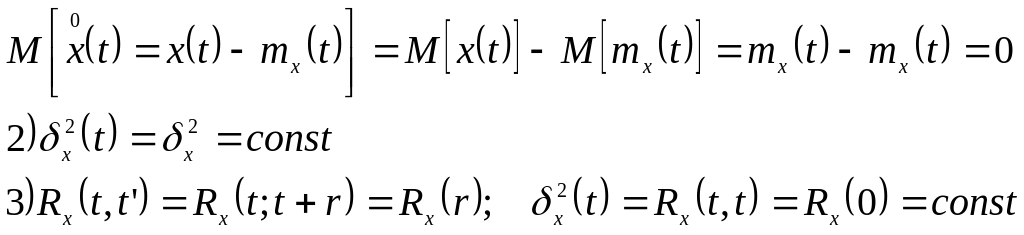
5 Нормальный закон распределения. Использование таблиц и интеграла вероятностей.

Если С.В. формируется под воздействием большого числа факторов, либо как сумма большого числа НСВ (независимых случайных величин) , то чаще всего его закон распределения как норм. закон.

Для норм. закона плотность распределения описывается следующим соотношением:

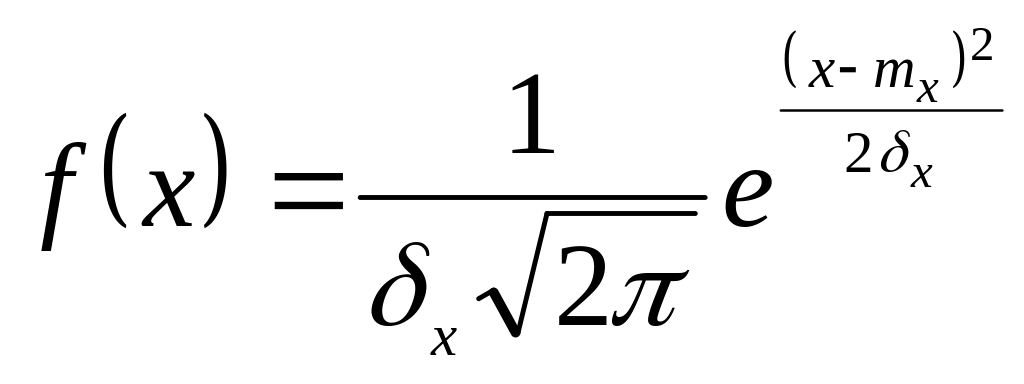норм. функция распределения; плотность распределения;

интеграл вероятностей гаусса

Этот интеграл не берется от элементарной функции. Данный интеграл вычисляется численно и для пользования таблицами перем-ая x-нормируется, вводиться переменная t.

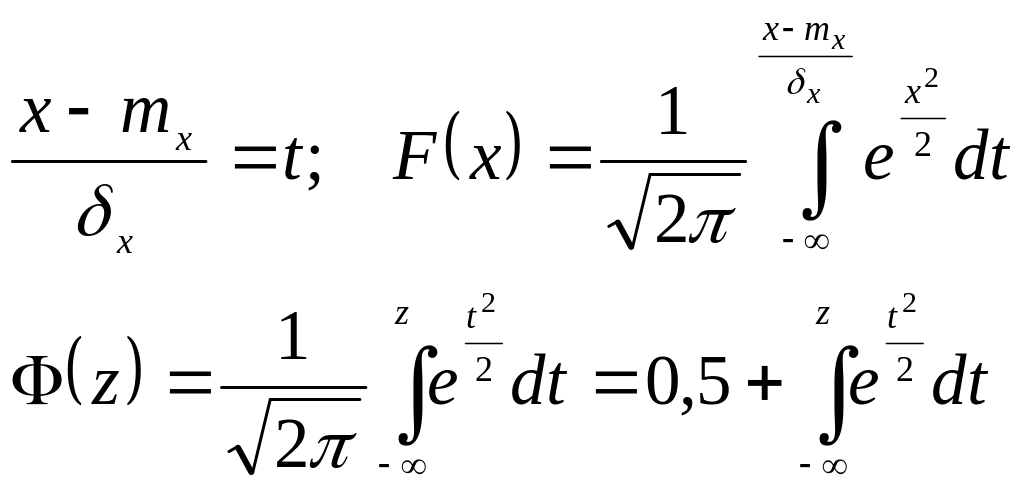
Если нам нужно вычислить на отрезке

Линейное преобразование:

Характеристи́ческая фу́нкция случа́йной величины́ — один из способов задания распределения. Характеристические функции могут быть удобнее в тех случаях, когда, например, плотность или функция распределения имеют очень сложный вид. Также характеристические функции являются удобным инструментом для изучения вопросов слабой сходимости (сходимости по распределению).

Пусть есть случайная величина X с распределением . Тогда характеристическая функция задаётся формулой:

.

Пользуясь формулами для вычисления математического ожидания, определение характеристической функции можно переписать в виде:

,

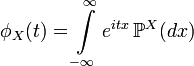то есть характеристическая функция — это обратное преобразование Фурье распределения случайной величины.

Если случайная величина X принимает значения в произвольном гильбертовом пространстве , то её характеристическая функция имеет вид:

,

где обозначает скалярное произведение в .

• Характеристическая функция однозначно определяет распределение. Пусть X,Y суть две случайные величины, и . Тогда 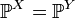. В частности, если обе величины абсолютно непрерывны, то совпадение характеристических функций влечёт совпадение плотностей. Если обе случайные величины дискретны, то совпадение характеристических функций влечёт совпадение функций вероятности.

• Характеристическая функция всегда ограничена:

.

• Характеристическая функция в нуле равна единице:

.

• Характеристическая функция всегда непрерывна: .

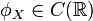• Характеристическая функция как функция случайной величины однородна:

.

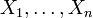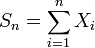• Характеристическая функция суммы независимых случайных величин равна произведению их характеристических функций. Пусть суть независимые случайные величины. Обозначим . Тогда

.