5.3.5. Смежно-групповые коды

Выше мы рассматривали групповые коды, в которых задана операция поразрядного сложения по модулю 2. В ряде случаев для придания кодовым комбинациям дополнительных признаков используют поразрядное сложение по модулю 2 с инвертированием некоторых элементов. По отношению к групповому коду полученный код может быть отождествлен со смежным классом разложения группы по подгруппе, являющейся кодом, с образующим в виде комбинации с единицами на местах инвертируемых элементов и нулями во всех остальных разрядах.

В силу этого рассматриваемые коды получили название смежно-групповых.

Следует иметь в виду, что смежно-групповой код существует только в дискретном канале. Процедуры кодирования и декодирования при использовании смежно-групповых кодов осуществляются как аналогичные операции для групповых кодов. Инвертирование разрядов кодовой комбинации, т.е замена ее комбинацией смежного класса, выполняется на выходе кодера, и обратная операция- на входе декодера.

В связи с этим важно оценить повлияет ли переход от кодовых комбинаций к комбинациям смежного класса в дискретном канале на помехоустойчивость кода.

Теория групповых кодов полностью определяет свойства смежно-групповых кодов. Легко показать, что корректирующие свойства смежно-групповых кодов не отличаются от корректирующих свойств групповых кодов, из которых они получены. Рассмотрим кодовое расстояние в смежно-групповом коде. и - две произвольные комбинации смежно-группового кода с образующим с. Тогда каждая из этих комбинаций может быть представлена через комбинацию исходного группового кода:

. Их сумма:

равна комбинации исходного группового кода. Следовательно, расстояние между двумя любыми комбинациями смежно-группового кода определяется весом одной их кодовых комбинаций исходного группового кода.Итак, справедлива теорема:

Теорема 5.2. Кодовые расстояния смежно-группового кода совпадают с кодовыми расстояниями исходного группового кода. Это означает, что помехоустойчивость смежно-групповых кодов эквивалента помехоустойчивости исходных групповых кодов.

5.3.6. Задачи

1. Показать, что условие существования совершенных кодов задается границей Хэмминга.

2. Какие из перечисленных кодов, удовлетворяют условию совершенных

а)(23,12)-код, dmin=7,

б)(17,9)-код,dmin=7,

в)(63,57)-код,dmin=3,

г)(63,51)-код,dmin=5,

д)(7,4)-код,dmin=3.

3. Чему равно минимальное кодовое расстояние для (7, 4) – кода с проверочной матрицей

.

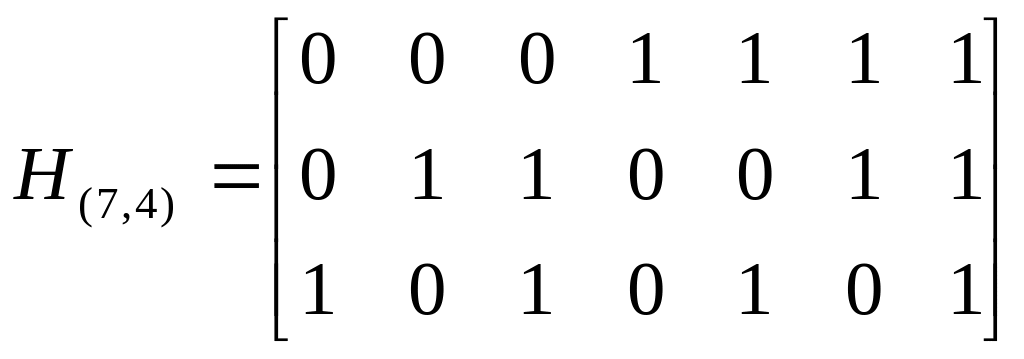4. Проверить, принадлежат ли комбинации

0 1 1 0 0 1 0 и 1 0 0 1 1 0 1 к одному смежному классу (7, 4) – кода.

5.Оценить выигрыш по достоверности, обеспечиваемой (7, 4) – кодом, с d_min=3 по сравнению с простым семиэлементным кодом при исправлении и при обнаружении ошибок в канале с группирующими ошибками.

5.4. Примеры групповых кодов

5.4.1. Коды с единственной проверкой на четность

Простейший помехоустойчивый код для обнаружения ошибок можно получить, если ввести одну проверку на четность по всем элементам без избыточного сообщения, т.е. к передаваемому k – разрядному сообщению добавить еще один разряд, являющийся результатом суммирования всех элементов сообщения по модулю 2:

.

Полученный таким образом код является групповым и может быть обозначен (n, n-1) –код. Проверочная матрица (n, n-1) –кода состоит из одной строки и n столбцов. В качестве всех столбцов проверочной матрицы записываются 1, т.к. проверкой охватываются все элементы сообщения: .

Так как все столбцы проверочной матрицы одинаковы, то минимальное кодовое расстояние в (n, n-1) –коде равно 2, т.е. (n, n-1) –код гарантийно обнаруживает все однократные ошибки.

В каждой кодовой комбинации (n, n-1) –кода имеется четное число единиц. Таким образом, код дополнительно может обнаружить все ошибки, приводящие к изменению четности единиц, т.е. ошибки любой нечетной кратности.

Итак, (n, n-1) –коды обнаруживают все ошибки нечетных кратностей

Ошибки же четной кратности кодом не обнаруживаются. Доля необнаруживаемых кодом ошибок составляет , т.к. не обнаруживается ровно половина возможных ошибочных трансформаций.

Пример 5.12. Одним из первых помехоустойчивых кодов, нашедших применение на практике, является шестиэлементный код, получаемый из пятиэлементного простого кода добавлением одного избыточного элемента так, чтобы число единиц и нулей в каждой кодовой комбинации было четным.

Этот код является групповым (6, 5) – кодом. Порождающая матрица и матрица проверок этого кода имеют вид:

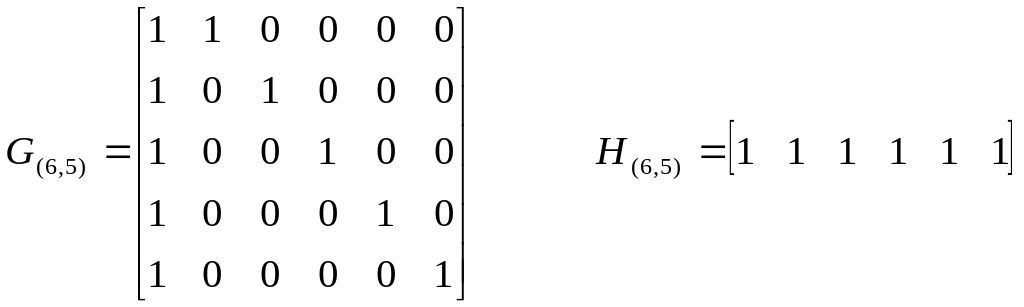
По виду матрицы Н_(6,5) можно сделать вывод, что данный код имеет d_min=2, т.е. гарантийно обнаруживает все одиночные ошибки.

Построение кодирующего и декодирующего устройств для (6, 5) – кода, как для циклического кода с порождающим многочленом , будет показано ниже.

Вероятность необнаружения ошибок (n, n-1) –кода в канале с группированием равна

.

Вероятность появления ошибок в n – элементной комбинации простого кода равна:

.

Подсчитаем выигрыш по достоверности, обеспечиваемый (n, n-1) –кодами:

.

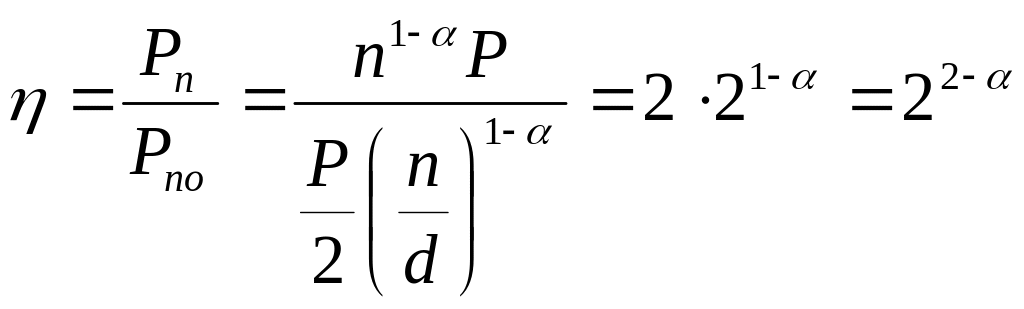Учитывая пределы изменения показателя группирования , находим, что (n, n-1) – коды обеспечивают повышение достоверности по сравнению с простыми кодами той же длины в раза.