Каждая компонента имеет характерное наименование

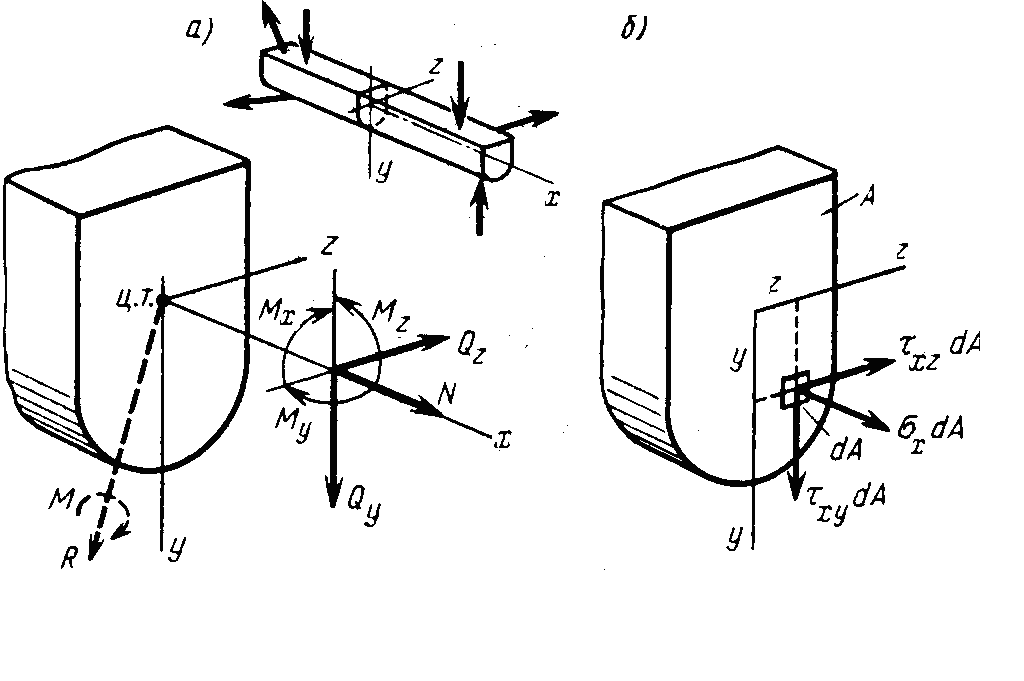
Рис. 1.9. Внутренние усилия и напряжения в поперечном сечении стержня

Nx - продольная сила в сечении, связанная с деформацией растяжения или сжатия;

Q_y Q_z — поперечные силы в сечении, возникающие

при стремлении к срезу по поперечному сечению в напра­влении осей y z;

Мz, My — изгибающие моменты в сечении относите­льно осей z и у, возникающие при изгибе соответственно в плоскостях xу и xz;

М_x — крутящий момент, возникающий при стремле­нии к относительному повороту двух частей стержня вокруг оси x.

Выразим внутренние усилия через напряжения, дейст­вующие в поперечном сечении, предполагая их извест­ными в каждой его точке (рис. 1.9, б). Элементарные силы

на площадке dA в этой точке будут _xdA, _xzdA и _xydA.

Проецируя все элементарные силы на оси х, у. z и сум­мируя моменты этих сил относительно этих осей по всему сечению, получим выражения внутренних усилий через напряжения:

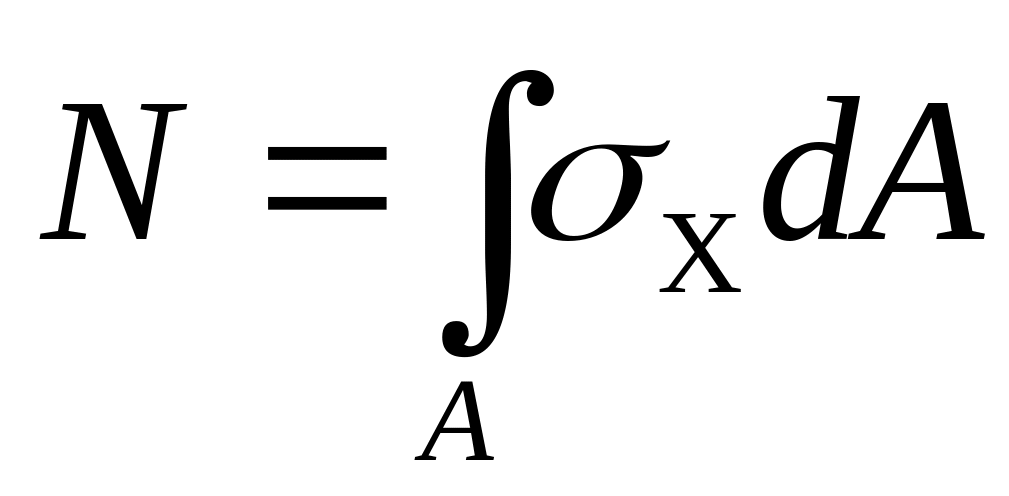
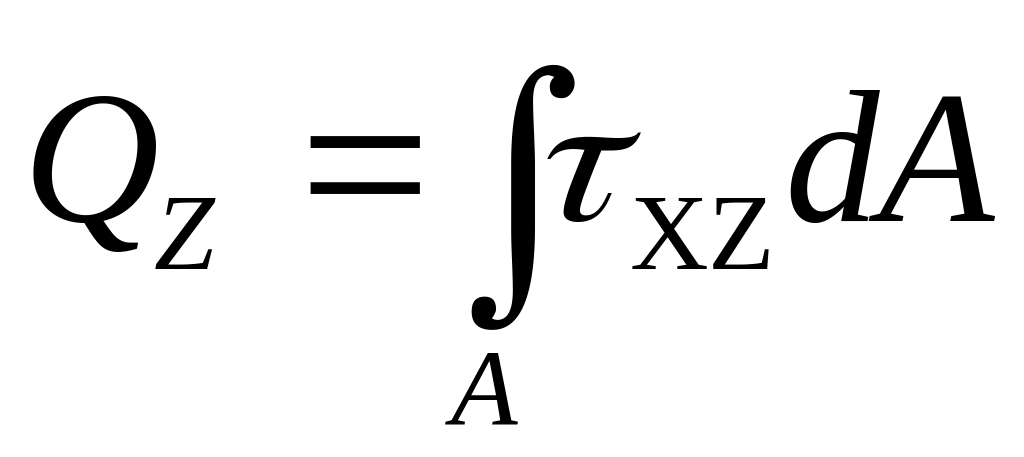
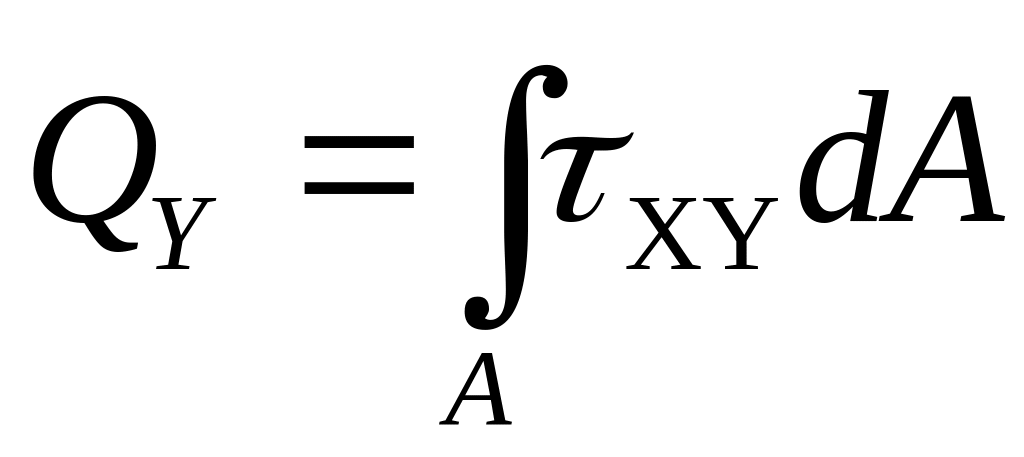
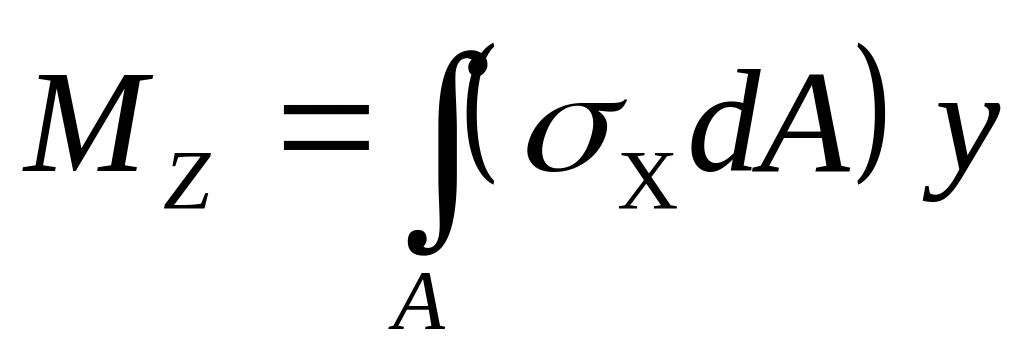
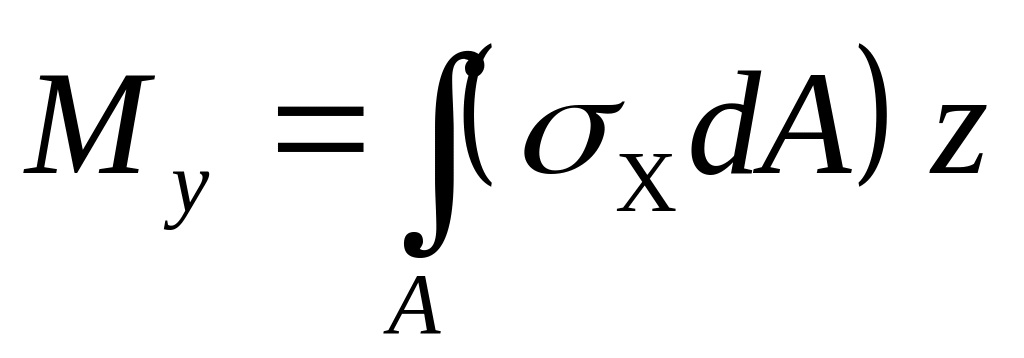
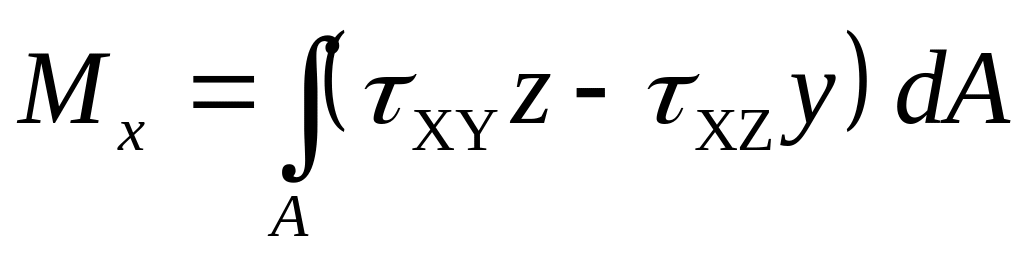
1.10. Метод определения внутренних усилий в поперечных сечениях стержней

При действии на тело внешних сил оно деформирует­ся. Следовательно, меняется взаимное расположение ча­стиц тела; в результате этого возникают дополнительные силы взаимодействия между частицами. Эти силы вза­имодействия в деформированном теле будем называть внутренними силами (усилиями). Для решения задач со­противления материалов необходимо уметь определять значение и направление внутренних усилий, например в задачах, где оценивается прочность конструкции. При их определении применяется метод сечений.

Первыми в середи­не XIX в. метод сечений ввели не­мецкие инженеры А. Риттер и Д. Шведлер, ко­торые этот метод использовали для определения уси­лий в стержнях ферм

Рассмотрим тело, имеющее форму бруса и находящееся в равновесии под действием системы внешних сил f_i (самоуравновешенной системы сил). Пусть требуется

определить внутренние усилия в произвольном сечении а — а этого бруса (рис. 2.1, а). Мысленно рассечем его по сечению а — а на две части и отбросим одну из частей, например часть I (обычно оставляется та часть, при рассмотрении которой получается более простое реше­ние).

Оставшаяся часть II в общем случае не будет нахо­диться в равновесии. Для сохранения этой части бруса в равновесии необходимо к ней приложить систему уси­лий, распределенных по сечению а — а (рис. 2.1, б). Эти усилия и есть внутренние усилия в сечении а — а рассмат­риваемого бруса. Они заменяют собой действие отбро­шенной части I (вместе с приложенными к ней внешними силами) на оставшуюся часть II . Внутренние усилия, согласно закону о равенстве действия и противодействия, которые приложены к части II в сечении а — а, равны и противоположны по направлению внутренним усилиям, действующим на часть I в том же сечении.

В соответствии с правилами статики приведем систему внутренних усилий, действующих на часть П в сечении а- а, к главному вектору R и главному моменту М, приложенным в центре тяжести этого сечения. Выберем систему координат х, у, z с началом в том же центре тяжести (точка О). Ось х направим по внешней нормали

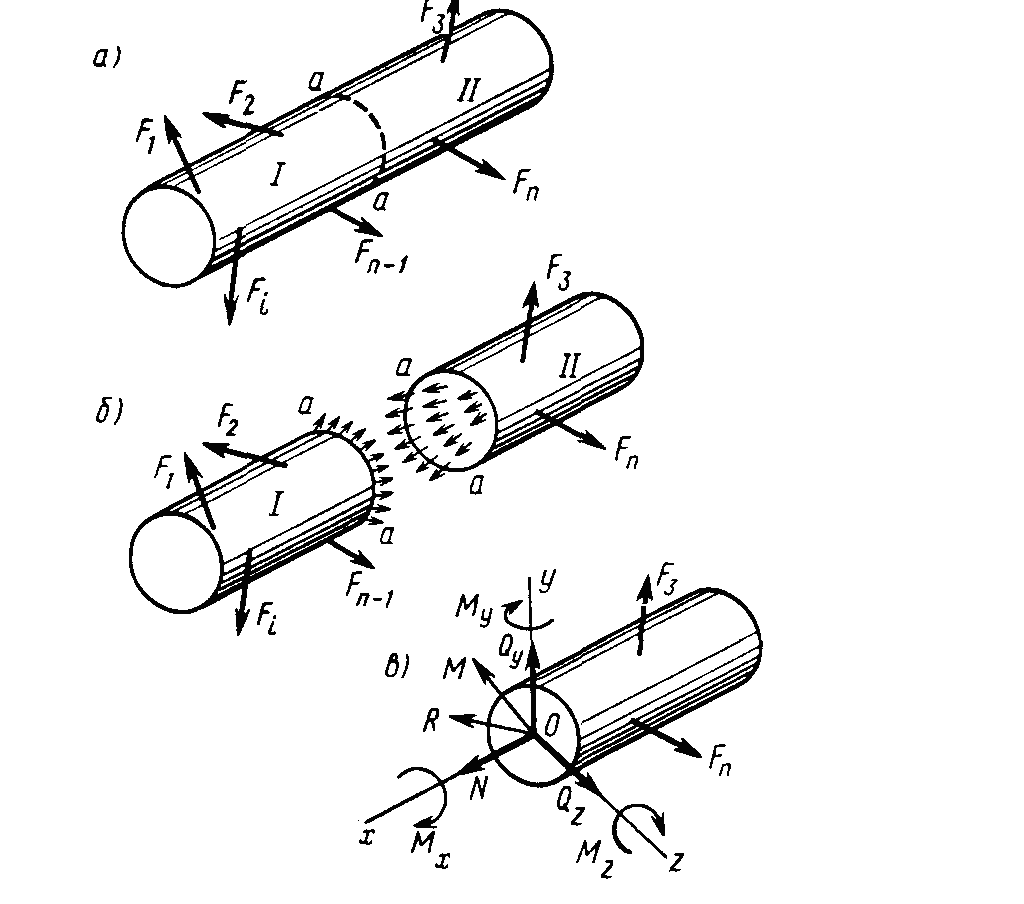
Рис. 2.1. Определение внутренних усилий методом сечений

Внутренние усилия.Разложим главный вектор и главный момент на со­ставляющие по координатным осям х, у, z. В результате получим шесть составляющих, которые принято назы­вать внутренними силовыми факторами или внутренними усилиями.

Составляющие главного вектора носят названия:

усилие вдоль оси х — продольной силы N;

усилия вдоль осей z и у — поперечных сил Q_z, и Qy со­ответственно.

Составляющие главного момента носят названия:

момент относительно продольной оси x — крутящего момента М_x = М_кр,

моменты относительно осей z и у — изгибающих мо­ментов М_z и My соответственно.

Таким образом, после приложения в сечении а — а к части II усилий, заменяющих собой действие отброшен­ной части (в общем случае шести силовых факторов), оставшаяся часть //, нагруженная и приложенными к ней внешними силами, находится в равновесии. Поэтому для части II можно записать шесть уравнений равновесия:

Уравнения равновесия для оставшейся части стержня:

ΣX=0; ΣY=0 ; ΣZ=0;

ΣM_x=0; ΣM_y=0; ΣM_z=0

Напомним основные правила составления уравнений равновесия:

1. Проекция силы ва ось равна произведению силы на косинус угла между направлением силы и положительным направлением оси.

2. Бели сила перпендикулярна оси, то ее проекция на ось равна нулю.

3. Момент силы относительно оси равен произведению проекции этой силы на плоскость, перпендикулярную оси, на плечо силы.

4. Момент силы относительно оси равен нулю:

а) если сила параллельна оси;

б) если линия действия силы пересекает ось.

Из первых трех уравнений равновесия (2.1) соответст­венно находим усилия б», Qy и N, а из трех послед­них — соответственно моменты At,, My и Mi.

Заметим, что знак у этих усилий, получаемый из реше­ния уравнений (2.1), указывает на правильность (знак плюс) или неправильность (знак минус) выбранных напра­влений внутренних усилий.

Таким образом, метод сечений дает возможность определить в сечении направление и значение равнодейст­вующих внутренних усилий (или их компонент). Закон же распределения внутренних усилий по сечению остается неизвестным. Для решения этого вопроса необходимо знать, как деформируется данный брус под действием внешних сил, приложенных к нему.

Применение метода сечения для определения значе­ний и направлений внутренних усилий рассмотрим на следующем примере.

Пример 2.1. Для пространственного стержня (рис. 2.2, а) опреде­лить значения и направления внутренних усилий в сечениях I—I и II—II.

Решение. Для определения значений и направлений внутренних усилий в сечениях I—I и II—II применим метод сечений.

Сечение I—I. Рассечем пространственный стержень в сечении I—I плоскостью, которая перпендикулярна оси стержня ВС (рис. 2.2, б). Одну часть стержня, например содержащую заделку, отбросим и дейст­вие ее на оставшуюся часть заменим шестью внутренними усилиями N, Qx- Qy и Mх, M_у, Mz, приложенными в сечении I—I.

Заметим, что в стержне, закрепленном при помощи жесткой задел­ки, целесообразно оставлять ту часть стержня, которая не закреплена, так как тогда не требуется определять опорные реакции.

Далее выберем прямоугольную систему осей х, у, z, совместив начало координат с центром тяжести сечения I—I Ось x направим вдоль оси рассеченного стержня ВС (в сторону внешней нормали сече­ния), а оси z и у расположим в плоскости его поперечного сечения, как показано на рис. 2.2, 6. Такой выбор осей является обязательным.

Рис.2.2.

Внутренние усилия Qz, Qy, N направим вдоль соответствующих поло­жительных осей z, у, x, внутренние усилия М_x, My, M_z: — по ходу

часовой стрелки при взгляде на оставшуюся часть со стороны положи­тельного направления тех же осей. Такие направления внутренних сило­вых факторов будем считать положительными.

Часть стержня, нагруженная внешними силами F, 2F и усилиями, приложенными в сечении I—I, находится в равновесии (рис. 2.2, 6). Для этой части стержня составим шесть уравнений равновесия, из решения которых определим внутренние усилия в сечении I—I:

ΣX=0; 2F + N =0; N = - 2F

ΣY=0; -F + Q_y = 0; Q_y = F

ΣZ=0; Q_z = 0;

ΣM_x=0; F*a + M_x =0; M_x = - F*a

ΣM_y=0; M_y=0;

ΣM_z=0; - F*2a + M_z=0; M_z = F*2a

Таким образом, в сечении I—I действует четыре внутренних усилия (Q_z =0 Му=0), причем два из них N и Мх,—в направлении,

противоположном принятому (на рис. 2.2, действительные направле­ния их показаны пунктиром).

Сечение II—II. Рассечем стержень в сечении II—II плоскостью, перпендикулярной оси стержня CD. Часть стержня, содержащую жест­кое закрепление, отбросим. Выберем систему координат х, у, z и дейст­вие отброшенной части на оставшуюся заменим шестью внутренними усилиями, как показано на рис. 2.2, в. Эта часть стержня находится в равновесии; составим для нее уравнения равновесия:

ΣX=0; -F + N =0; N = F

ΣY=0; Q_y = 0;

ΣZ=0; 2F + Q_z = 0; Q_z = - 2F

ΣM_x=0; M_x =0;

ΣM_y=0; -2F*a - F*2a + M_y=0; M_y = 4F*a

ΣM_z=0; F*a + M_z=0; M_z = -F*a

Следовательно, в сечении II—II возникает четыре внутренних уси­лия (Qy =0, M_x=0), причем два из них Qz и Mz — направлены в об­ратную сторону (рис. 2.2, в).