Свойства бесконечно малых

1) Бесконечно малая последовательность является ограниченной последовательностью.

Действительно, если бы она не была ограниченной, то вне достаточно малой окрестности нуля находилось бы бесконечное множество членов последовательности.

2) Любая конечная(конечное количество операций суммирования) сумма бесконечно малых последовательностей есть также бесконечно малая последовательность.

3) Произведение бесконечно малой последовательности на любую ограниченную последовательность или на любое конечное, отличное от нуля, число есть бесконечно малая последовательность.

4) Линейная комбинация счетного числа бесконечно малых последовательностей является бесконечно малой последовательностью.

3. Последовательность {xn} называется сходящейся, если существует такое вещественное число а, что последовательность {xn−a} является бесконечно малой. Если последовательность {xn→a } является сходящейся и имеет своим пределом число a, то символически это записывают так:limn→∞xn=a или xn→a  при n→∞ 

Основные свойства сходящихся последовательностей:

1.          Сходящаяся последовательность имеет только один предел;

2.          Сходящаяся последовательность ограничена;

3.          Если , то ;

4.          При любых постоянных  и   ;

5.          ;

6.          Если ,  и , то ;

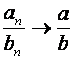7.          Если , то ;

8.          Если  и , то ;

9.          Если , то .

4. Монотонные последовательности.

Определение

1. Последовательность x_n возрастает (убывает), если  n N x_n<x_n+1(x_n>x_n+1)

2. x_n не убывает (не возрастает), если  n N x_n  x_n+1 (x_n  x_n+1)

Теорема 12 (теорема Вейерштрасса). Неубывающая последовательность сходится  когда она ограничена сверху

Теорема о переходе к пределу в неравенстве

Пусть и ; ,Тогда Док-во:  предложим противное: > < ;по определению пределов:

(*) <

(**) <

будут выполнены (*) и (**)

< < < < ;т.е

< ,что противоречит условию значит < не верно,а -верно(утверждение теоремы);

если в условии теоремы записать,что < ; то

<  

>

=

Терема о сжатой переменной также о ( двух милиционерах )

5. Число e выражается через предел следующим образом:

Это число является трансцендентным и приблизительно равно 2,718281828... (2.7, затем два раза год рождения Л.Н.Толстого). Выполнив подстановку , где , получим альтернативную формулу для данного предела:

Здесь мы имеем дело со степенными выражениями, когда и основание и степень стремятся к числу a (или к бесконечности). Во многих случаях такие пределы удобно вычислять, предварительно логарифмируя функцию под знаком предела.

Логарифм по основанию e (e - трансцендентное число, приближенно равное 2,718281828...) называется натуральным логарифмом. Натуральный логарифм числа x обозначается ln x

6. Теорема Больцано-Вейерштрасса

     Теорема. Из любой ограниченной последовательности можно выделить сходящуюся подпоследовательность.

     Доказательство. Так как последовательность ограничена, то она имеет хотя бы одну предельную точку x. В таком случае из этой последовательности можно выделить подпоследовательность, сходящуюся к точке x.

Коши критерий сходимости последовательности

Пусть задана числовая последовательность {x_n}. Эта последовательность сходится тогда и только тогда, когда для любого числа ε > 0 существует номер N такой, что при всех n > N  и любых натуральных m выполняется неравенство (т.е. расстояние между членами последовательности с номерами n  и n+m меньше ε) – критерий Коши сходимости последовательности.

Также отметим, что последовательность, удовлетворяющая критерию сходимости Коши, называется также фундаментальной или последовательностью Коши.

7. Пусть f: X → R и x₀ - предельная точка множества X.

(Гейне): Функция f имеет предельное значение при x → x₀ (или в точке x₀), если существует такое число , что для произвольной последовательности (x_n) значений , сходящейся к точке x₀, соответствующая последовательность значений функции (f(x_n)) сходится к точке A.

(Коши): Функция f имеет предел при x → x₀, если

При этом число A называем пределом (или предельным значением) функции f в точке x₀ и записываем

или f(x) → A при x → x₀.

Определение Гейне и Коши эквивалентны.

Введем понятие одностороннего предела.

(Гейне): Функция f имеет в точке x₀ предел слева (справа), если существует такое число , что для произвольной последовательности (x_n) значений x, a < x_n < x₀ (x₀ < x_n < b), сходящейся к точке x₀ при n → ∞, соответствующая последовательность (f(x_n)) значений функции f сходится к точке A.

(Коши): Функция f имеет в точке x₀ предел слева (справа), если

Бесконечно малые.

Переменная называется бесконечно малой, если для любого существует такое значение , что каждое следующие за ним значение будет по абсолютной величине меньше .

Если - бесконечно малая то говорят, что стремится к нулю, и пишут: .

Бесконечно большие.

Переменная x называется бесконечно большой, если для всякого положительного числа c существует такое значение , что каждое следующее за ним x будет по абсолютной величине больше . Пишут:

Величина, обратная к бесконечно большой, есть величина бесконечно малая, и обратно.

  Перечислим основные виды неопределенностей:

      Под неопределенностью вида     понимается отношение двух бесконечно малых величин. Неопределенность вида       возникает при делении одной бесконечно большой величины на другую. Аналогично интерпретируются и другие формы неопределенностей.

8. Предел функции. Число L называется пределом функции  y = f ( x ) при  x, стремящемся к  a :

если для любого  > 0 найдётся такое положительное число = ( ), зависящее от  , что из условия | x  a | < следует  |  f ( x ) – L | < 

Это определение означает, что L есть предел функции  y = f ( x ), если значение функции неограниченно приближается к  L , когда значение аргумента  x приближается к  a. Геометрически это значит, что для любого  > 0  можно найти такое число  , что если  x  находится в интервале ( a  a  ), то значение функции лежит в интервале ( L  ,  L + ). Отметим, что в соответствии с этим определением аргумент функции лишь приближается  к  a , не принимая этого значения! Это следует учитывать при вычислении предела любой функции в точке её разрыва, где функция не существует.

К основным свойствам пределов функции относят: - предел постоянной величины, который равен самой постоянной величины; - предел суммы, который равен сумме пределов самих функций. Также по аналогии и предел разности функций равен разности пределов данных функций; - предел суммы множества функций равен также сумме пределов таких функций. По аналогии рассчитывает и предел нескольких функций, который равен разности пределов данных функций. - повышение предела произведения функции (постоянного коэффициента) на знак предела. - произведению пределов функций равен предел произведения двух функций; - расширенное свойство предела произведения, которое в том заключается, что предел произведения функций равен и произведению пределов данных функций - предел частного функций равен отношению пределов данных функций, но только в том случае, если предел знаменателя нулю не равен; - предел функции степенной, где действительным числом является степень р; - предел функции показательной, при которой основание b больше 0; - предел функции логарифмической, в которой основание b больше 0; - теорема «двух милиционеров», при которой «зажатой» остается функция f(x)между другими двумя функции, которые также стремятся к пределу А. Все перечисленные свойства пределов позволяют исходный предел функции свести к уже известному, чтобы получить ответ.