4. Измерение параметров линейной зависимости

Если есть основания предполагать, что исследуемая зависимость двух величин Y и X является линейной, то есть удовлетворяет формуле

, (4.1)

и экспериментальный график зависимости y(x) это подтверждает, то есть через доверительные интервалы всех экспериментальных точек можно провести прямую линию, то результаты измерения величин Y и X (значения координат экспериментальных точек) позволяют измерить параметры линейной зависимости k и b. Это можно сделать, по крайней мере, двумя способами.

1. Графический способ измерения параметров прямой линии

• Надо провести прямую линию на графике так, чтобы она пересекла доверительные интервалы всех точек и при этом как можно ближе прошла ко всем точкам (см. в качестве примера график на рисунке 4.1). После этого можно приступить к измерению k и b.

• k представляет собой угловой коэффициент прямой, поэтому его можно найти как отношение приращения функции F к приращению аргумента x. Для этого надо взять на экспериментальной прямой две произвольные точки 1 и 2, определить их координаты 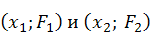, а затем поделить разность ординат на разность абсцисс:

• . (4.2)

О братите внимание: точки 1 и 2 – это не экспериментальные точки, а просто две любые (произвольные) точки, лежащие на прямой. Для большей точности измерения углового коэффициента желательно, чтобы точки 1 и 2 были подальше друг от друга. Например, на графике, показанном на рисунке 4.1, выделены точки с координатами: 1 (0; 5), 2 (11; 47). При этом получается: .

• b – это свободный член уравнения прямой линии. Он равен длине отрезка, который прямая линия графика отсекает на оси ординат (на вертикальной оси), поэтому для измерения b надо довести экспериментальную прямую до вертикальной оси и определить ординату точки пересечения. На рисунке 4.1 точка пересечения – это точка 1, её ордината равна 5 мН. Таким образом, b = 5 мН.

Описанное правило измерения свободного члена b справедливо при условии, что началом координат выбрана точка (0; 0). Если же удобнее выбрать другое начало координат, то следует использовать другое правило: надо выбрать на экспериментальной прямой две произвольные точки 1 и 2, определить их координаты , а затем найти уравнение прямой, проходящей через эти точки. В аналитической геометрии уравнение прямой, проходящей через две заданные точки, записывают так:

. (4.3)

Преобразование этого уравнения к виду даёт:

,

откуда следует, что

. (4.4)

Рассмотрим для примера график, показанный на рисунке 4.2. На этом рисунке роль x выполняет объём газа V, а роль y – давление газа p. На прямой линии, проведённой через доверительные интервалы экспериментальных точек, выбраны две произвольные точки с координатами : 1 (20; 72), 2 (31; 97). Обратите внимание: точка 1 взята слева от всех экспериментальных точек, а точка 2 – справа. Расчёт по формулам (4.4) для выбранных точек даёт:

.

2. А налитический способ измерения параметров прямой линии

Он называется методом наименьших квадратов. Его идея в том, что среди всевозможных пар чисел k и b существует такая единственная пара, для которой сумма квадратов отклонений ординат экспериментальных точек от соответствующих ординат прямой линии с параметрами k и b, минимальна. Не рассматривая этот метод в деталях, приведём конечные выражения, позволяющие измерить k и b.

, (4.5)

где обозначено:

. (4.6)

В этих формулах n – число экспериментальных точек, а наборы чисел (x_i) и (y_i) – результаты измерений, то есть абсциссы и ординаты экспериментальных точек.

Проделав вычисления по формулам (4.6) и (4.5), следует провести на графике прямую линию. Для этого надо по формуле вычислить координаты двух произвольных (контрольных) точек 1 и 2, нанести эти точки 1 (x_, y_) и 2 (x_, y_) на график и соединить их прямой линией. Для повышения точности проведения линии следует выбирать контрольные точки 1 и 2 за пределами области, в которой расположены экспериментальные точки. Это значит, что значение x_ надо выбрать меньше самого маленького значения в наборе (x_i), а значение x_ – наоборот, больше самого большого значения в наборе (x_i). Если все вычисления проделаны верно, то прямая линия автоматически пройдёт оптимальным образом, то есть пересечёт доверительные интервалы всех экспериментальных точек и при этом будет максимально приближена к экспериментальным точкам.